T
Teach Me AnythingTMA
Video History
Page 6 / 43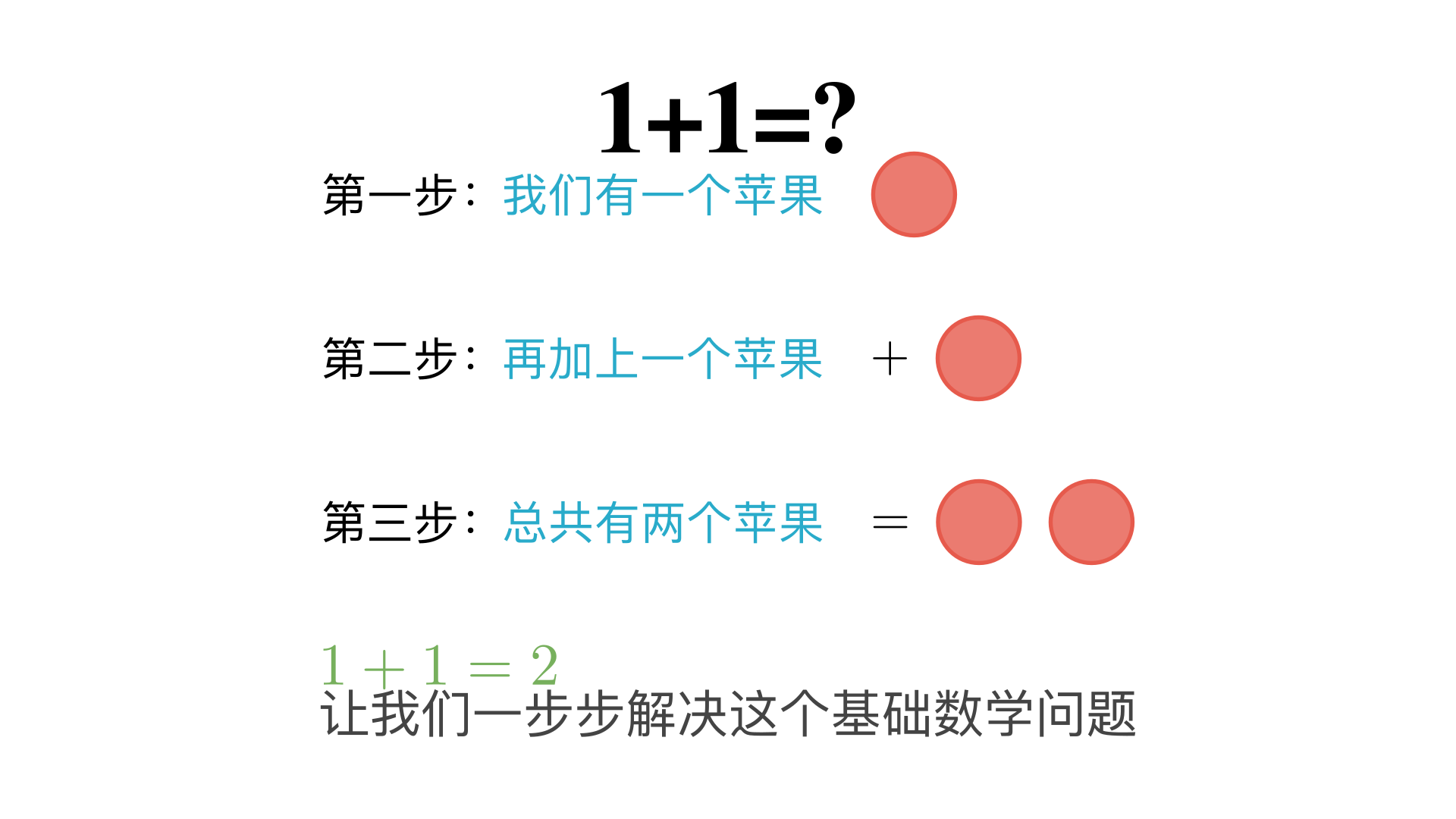
▶
1+1=?
▶
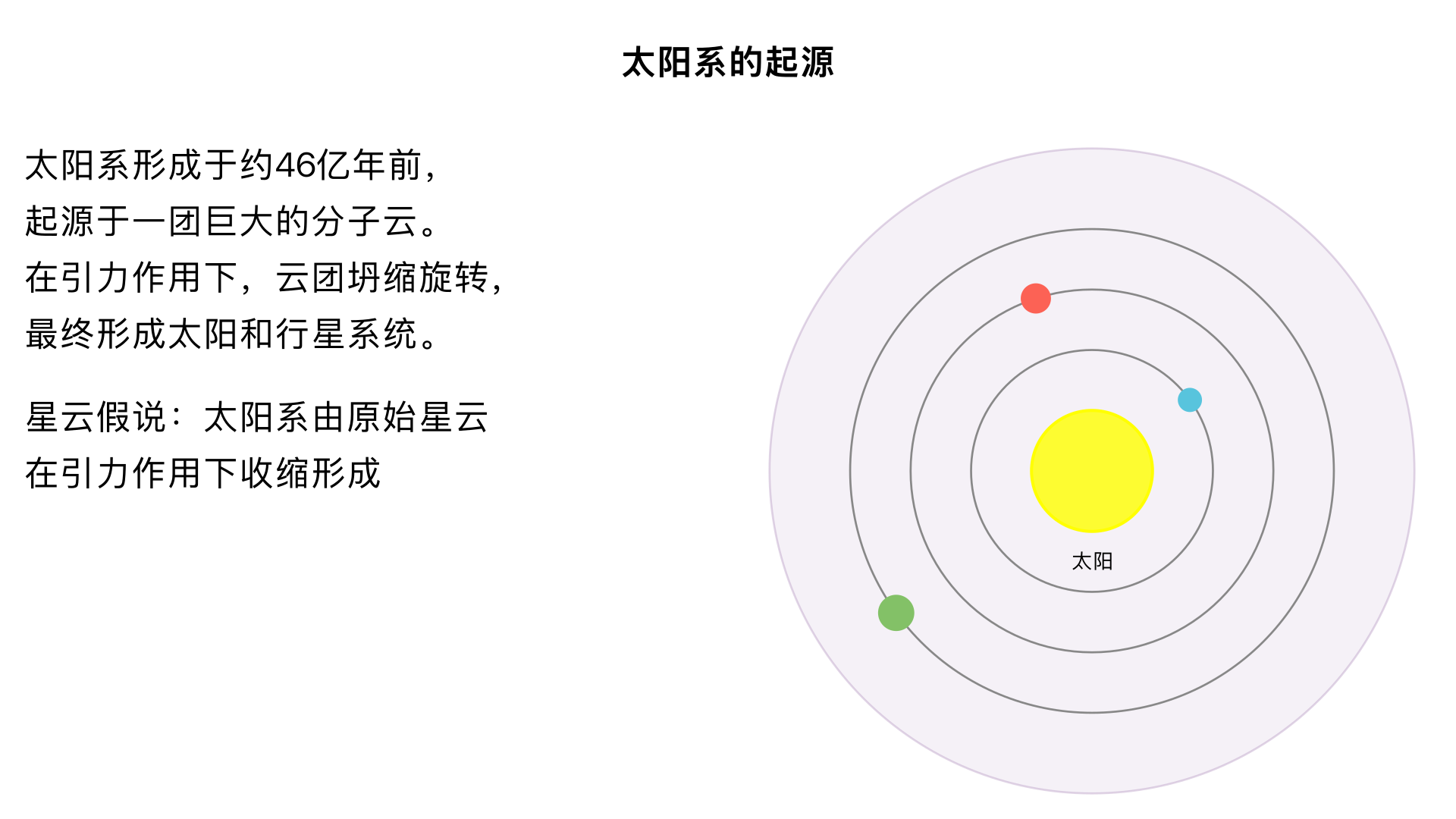
太阳系的起源
▶
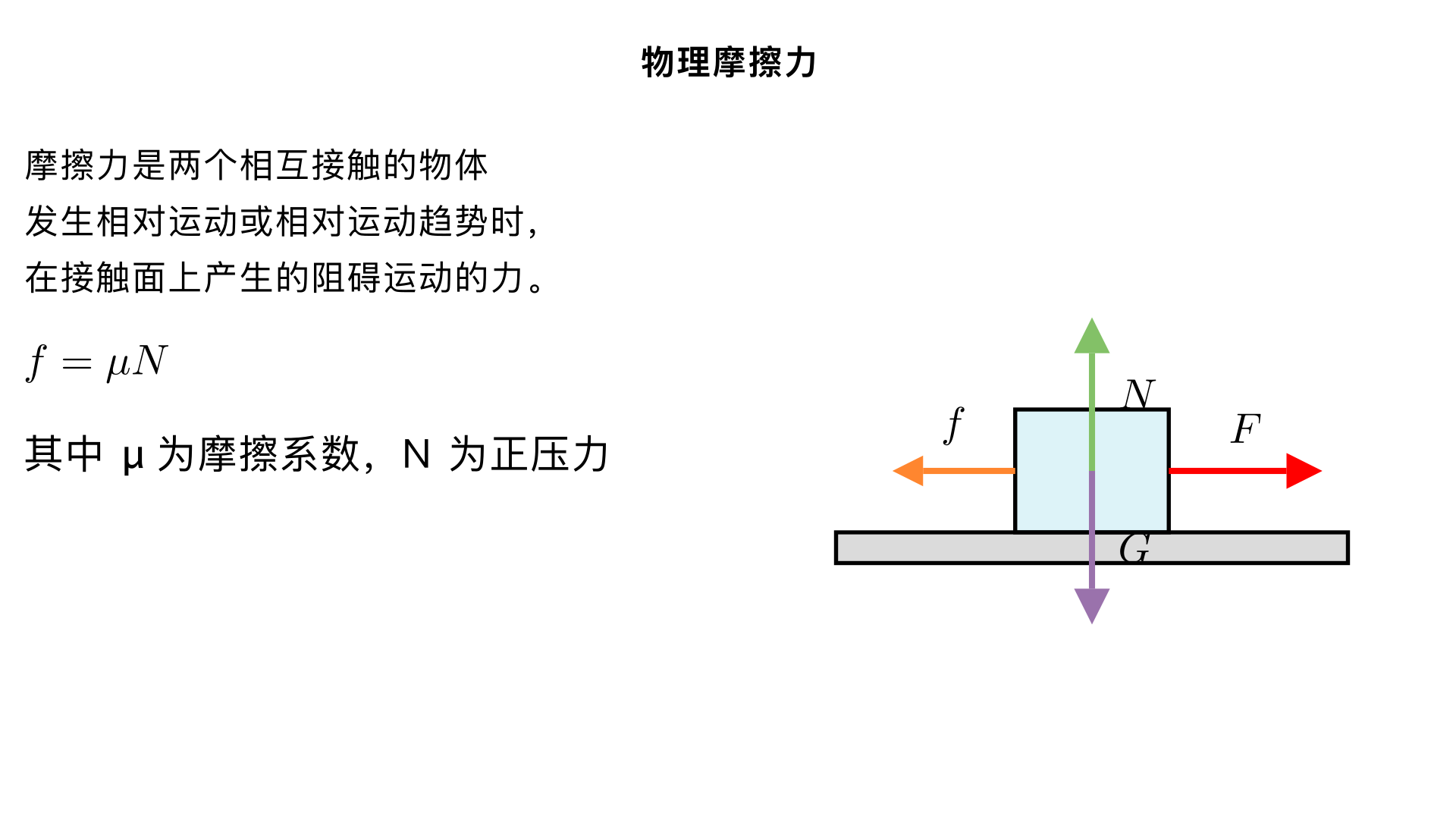
请生成一个解释物理摩擦力的视频
![八年级数学 / 因式分解 / 用提公因式法分解因式
一、核心概念(夯实基础)
1. 公因式的定义
一个多项式中各项都含有的公共因式,叫做这个多项式各项的公因式。
公因式的构成:① 系数部分:各项系数的最大公约数(若系数为负,取绝对值的最大公约数,最终公因式的符号由多项式首项符号决定,通常使首项为正);② 字母部分:各项中相同的字母,且取相同字母的最低次幂;③ 特殊情况:公因式可以是单项式,也可以是多项式(如
(a+b)
作为公共因式)。
示例:多项式
8a
3
b
2
−12ab
3
c
的公因式:系数部分:8 和 12 的最大公约数是 4;字母部分:相同字母为
a
(最低次幂
a
1
)、
b
(最低次幂
b
2
),无公共字母
c
;因此公因式为
4ab
2
。
2. 提公因式法的定义
如果一个多项式的各项含有公因式,那么就可以把这个公因式提取出来,将多项式化成两个因式乘积的形式,这种因式分解的方法叫做提公因式法。
本质:逆用乘法分配律(
ma+mb+mc=m(a+b+c)
,其中
m
为公因式)。
二、提公因式法的解题步骤(规范操作)
步骤 1:找公因式(关键步骤)
按 “系数→字母→多项式” 的顺序找,确保不遗漏:① 找系数的最大公约数(含符号处理);② 找相同字母的最低次幂;③ 若各项含有相同的多项式因式,将其视为一个整体作为公因式。
步骤 2:提公因式
用多项式的每一项除以公因式,得到另一个因式,公因式写在括号外,两个因式用乘法连接。
注意:提取公因式后,括号内的各项系数、字母次数要与原多项式对应,不能漏项。
步骤 3:验结果(避免出错)
用乘法分配律将分解后的式子展开,看是否与原多项式相等,若相等则分解正确。
三、典型例题(分层突破)
类型 1:公因式为单项式(基础题)
例 1:分解因式
6x
2
y−9xy
2
+3xy
步骤 1:找公因式
系数:6、-9、3 的最大公约数是 3;
字母:相同字母
x
(最低次幂
x
1
)、
y
(最低次幂
y
1
);
公因式为
3xy
。
步骤 2:提公因式
每一项除以
3xy
:
6x
2
y÷3xy=2x
,
−9xy
2
÷3xy=−3y
,
3xy÷3xy=1
;
因此分解结果:
3xy(2x−3y+1)
(注意:最后一项除以公因式得 1,不能漏写)。
步骤 3:验证
展开
3xy(2x−3y+1)=6x
2
y−9xy
2
+3xy
,与原多项式一致,正确。
例 2:分解因式
−4a
3
b
2
+6a
2
b−2ab
步骤 1:找公因式
首项为负,先提取 “-” 号,再找系数绝对值的最大公约数:4、6、2 的最大公约数是 2;
字母:相同字母
a
(最低次幂
a
1
)、
b
(最低次幂
b
1
);
公因式为
−2ab
(提负号后,括号内各项符号要改变)。
步骤 2:提公因式
−4a
3
b
2
÷(−2ab)=2a
2
b
,
6a
2
b÷(−2ab)=−3a
,
−2ab÷(−2ab)=1
;
分解结果:
−2ab(2a
2
b−3a+1)
。
类型 2:公因式为多项式(进阶题)
例 3:分解因式
3(x−y)−2(x−y)
2
步骤 1:找公因式
各项都含多项式因式
(x−y)
,最低次幂为
(x−y)
1
;
系数:3、-2 的最大公约数是 1;
公因式为
(x−y)
。
步骤 2:提公因式
3(x−y)÷(x−y)=3
,
−2(x−y)
2
÷(x−y)=−2(x−y)
;
分解结果:
(x−y)[3−2(x−y)]=(x−y)(3−2x+2y)
(括号内可整理,去括号后合并同类项)。
例 4:分解因式
a(x−3)+2b(3−x)
关键:注意
(3−x)=−(x−3)
,先统一公因式;
步骤 1:变形后找公因式
原式 =
a(x−3)−2b(x−3)
,公因式为
(x−3)
;
步骤 2:提公因式
分解结果:
(x−3)(a−2b)
。
四、易错点总结(避坑指南)
漏提系数的最大公约数:如将
4x
2
−6x
分解为
2x(x−3)
(错误,应为
2x(2x−3)
);
漏提相同字母的最低次幂:如将
x
3
y
2
−x
2
y
3
分解为
x
2
y(x−y
2
)
(错误,应为
x
2
y
2
(x−y)
);
提公因式后漏写 “1”:如将
2x+4
分解为
2(x)
(错误,应为
2(x+2)
);
符号错误:首项为负时未提负号,或提负号后括号内各项符号未改变;
公因式为多项式时未统一形式:如
(x−y)
和
(y−x)
需先转化为相同形式。
五、基础练习(巩固提升)
分解因式:
12x
3
y−18x
2
y
2
(答案:
6x
2
y(2x−3y)
)
分解因式:
−8a
2
b+12ab
2
−4ab
(答案:
−4ab(2a−3b+1)
)
分解因式:
5(x+2)−3(x+2)
2
(答案:
(x+2)(5−3x−6)=(x+2)(−3x−1)=−(x+2)(3x+1)
)
分解因式:
m(a−b)−n(b−a)
(答案:
(a−b)(m+n)
)
六、总结
提公因式法是因式分解的最基础、最常用方法,核心是 “找准公因式”,关键在于兼顾系数、字母、多项式因式的提取,同时注意符号和漏项问题。掌握此方法后,能为后续学习公式法、十字相乘法等复杂因式分解打下基础,解题时需遵循 “找→提→验” 的步骤,规范操作,避免易错点。](https://manimvideo.explanation.fun/video/cover/596037600963858433.png)
▶
八年级数学 / 因式分解 / 用提公因式法分解因式 一、核心概念(夯实基础) 1. 公因式的定义 一个多项式中各项都含有的公共因式,叫做这个多项式各项的公因式。 公因式的构成:① 系数部分:各项系数的最大公约数(若系数为负,取绝对值的最大公约数,最终公因式的符号由多项式首项符号决定,通常使首项为正);② 字母部分:各项中相同的字母,且取相同字母的最低次幂;③ 特殊情况:公因式可以是单项式,也可以是多项式(如 (a+b) 作为公共因式)。 示例:多项式 8a 3 b 2 −12ab 3 c 的公因式:系数部分:8 和 12 的最大公约数是 4;字母部分:相同字母为 a (最低次幂 a 1 )、 b (最低次幂 b 2 ),无公共字母 c ;因此公因式为 4ab 2 。 2. 提公因式法的定义 如果一个多项式的各项含有公因式,那么就可以把这个公因式提取出来,将多项式化成两个因式乘积的形式,这种因式分解的方法叫做提公因式法。 本质:逆用乘法分配律( ma+mb+mc=m(a+b+c) ,其中 m 为公因式)。 二、提公因式法的解题步骤(规范操作) 步骤 1:找公因式(关键步骤) 按 “系数→字母→多项式” 的顺序找,确保不遗漏:① 找系数的最大公约数(含符号处理);② 找相同字母的最低次幂;③ 若各项含有相同的多项式因式,将其视为一个整体作为公因式。 步骤 2:提公因式 用多项式的每一项除以公因式,得到另一个因式,公因式写在括号外,两个因式用乘法连接。 注意:提取公因式后,括号内的各项系数、字母次数要与原多项式对应,不能漏项。 步骤 3:验结果(避免出错) 用乘法分配律将分解后的式子展开,看是否与原多项式相等,若相等则分解正确。 三、典型例题(分层突破) 类型 1:公因式为单项式(基础题) 例 1:分解因式 6x 2 y−9xy 2 +3xy 步骤 1:找公因式 系数:6、-9、3 的最大公约数是 3; 字母:相同字母 x (最低次幂 x 1 )、 y (最低次幂 y 1 ); 公因式为 3xy 。 步骤 2:提公因式 每一项除以 3xy : 6x 2 y÷3xy=2x , −9xy 2 ÷3xy=−3y , 3xy÷3xy=1 ; 因此分解结果: 3xy(2x−3y+1) (注意:最后一项除以公因式得 1,不能漏写)。 步骤 3:验证 展开 3xy(2x−3y+1)=6x 2 y−9xy 2 +3xy ,与原多项式一致,正确。 例 2:分解因式 −4a 3 b 2 +6a 2 b−2ab 步骤 1:找公因式 首项为负,先提取 “-” 号,再找系数绝对值的最大公约数:4、6、2 的最大公约数是 2; 字母:相同字母 a (最低次幂 a 1 )、 b (最低次幂 b 1 ); 公因式为 −2ab (提负号后,括号内各项符号要改变)。 步骤 2:提公因式 −4a 3 b 2 ÷(−2ab)=2a 2 b , 6a 2 b÷(−2ab)=−3a , −2ab÷(−2ab)=1 ; 分解结果: −2ab(2a 2 b−3a+1) 。 类型 2:公因式为多项式(进阶题) 例 3:分解因式 3(x−y)−2(x−y) 2 步骤 1:找公因式 各项都含多项式因式 (x−y) ,最低次幂为 (x−y) 1 ; 系数:3、-2 的最大公约数是 1; 公因式为 (x−y) 。 步骤 2:提公因式 3(x−y)÷(x−y)=3 , −2(x−y) 2 ÷(x−y)=−2(x−y) ; 分解结果: (x−y)[3−2(x−y)]=(x−y)(3−2x+2y) (括号内可整理,去括号后合并同类项)。 例 4:分解因式 a(x−3)+2b(3−x) 关键:注意 (3−x)=−(x−3) ,先统一公因式; 步骤 1:变形后找公因式 原式 = a(x−3)−2b(x−3) ,公因式为 (x−3) ; 步骤 2:提公因式 分解结果: (x−3)(a−2b) 。 四、易错点总结(避坑指南) 漏提系数的最大公约数:如将 4x 2 −6x 分解为 2x(x−3) (错误,应为 2x(2x−3) ); 漏提相同字母的最低次幂:如将 x 3 y 2 −x 2 y 3 分解为 x 2 y(x−y 2 ) (错误,应为 x 2 y 2 (x−y) ); 提公因式后漏写 “1”:如将 2x+4 分解为 2(x) (错误,应为 2(x+2) ); 符号错误:首项为负时未提负号,或提负号后括号内各项符号未改变; 公因式为多项式时未统一形式:如 (x−y) 和 (y−x) 需先转化为相同形式。 五、基础练习(巩固提升) 分解因式: 12x 3 y−18x 2 y 2 (答案: 6x 2 y(2x−3y) ) 分解因式: −8a 2 b+12ab 2 −4ab (答案: −4ab(2a−3b+1) ) 分解因式: 5(x+2)−3(x+2) 2 (答案: (x+2)(5−3x−6)=(x+2)(−3x−1)=−(x+2)(3x+1) ) 分解因式: m(a−b)−n(b−a) (答案: (a−b)(m+n) ) 六、总结 提公因式法是因式分解的最基础、最常用方法,核心是 “找准公因式”,关键在于兼顾系数、字母、多项式因式的提取,同时注意符号和漏项问题。掌握此方法后,能为后续学习公式法、十字相乘法等复杂因式分解打下基础,解题时需遵循 “找→提→验” 的步骤,规范操作,避免易错点。
▶
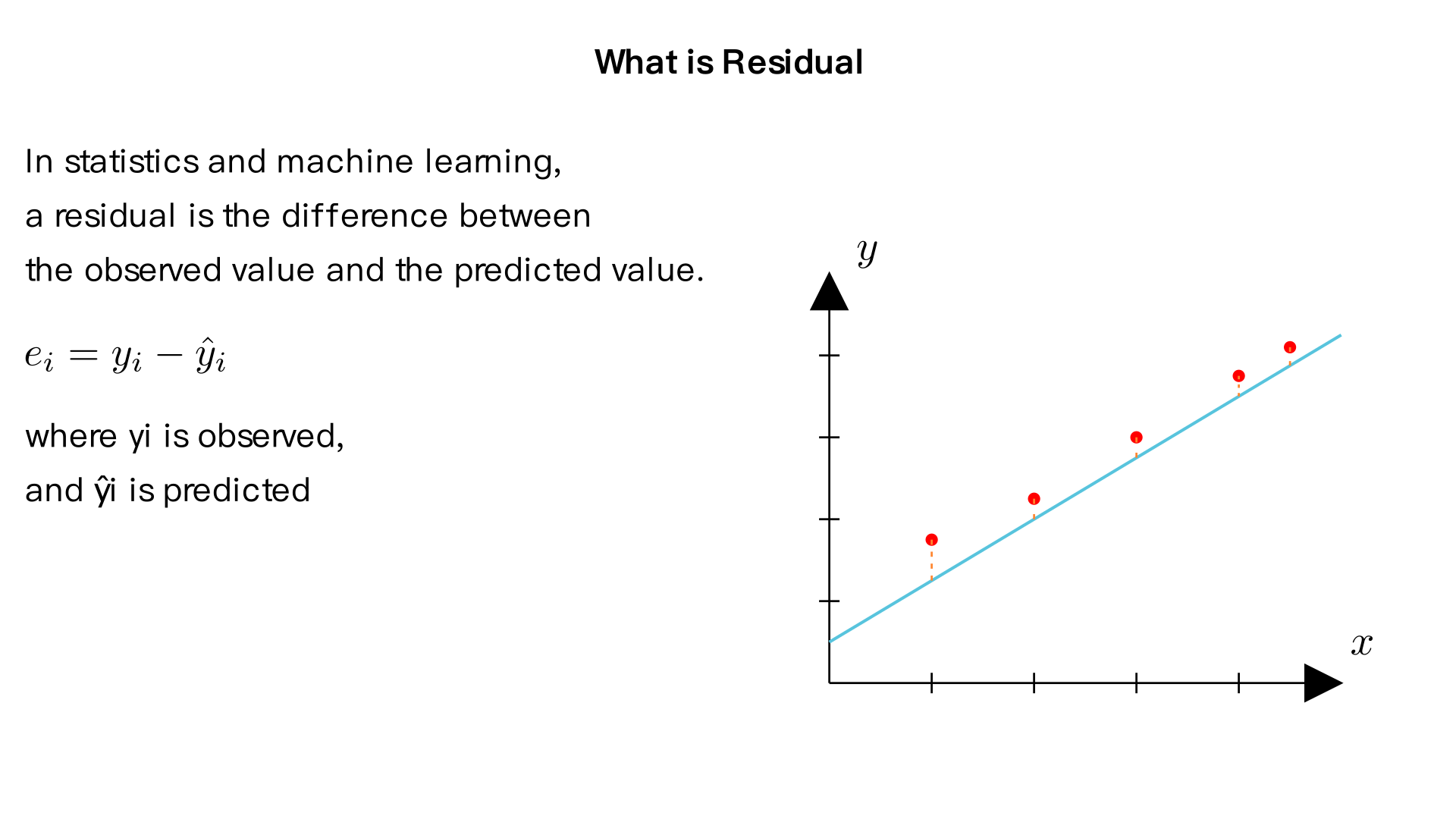
what is Residual

▶
什么是平均数
▶
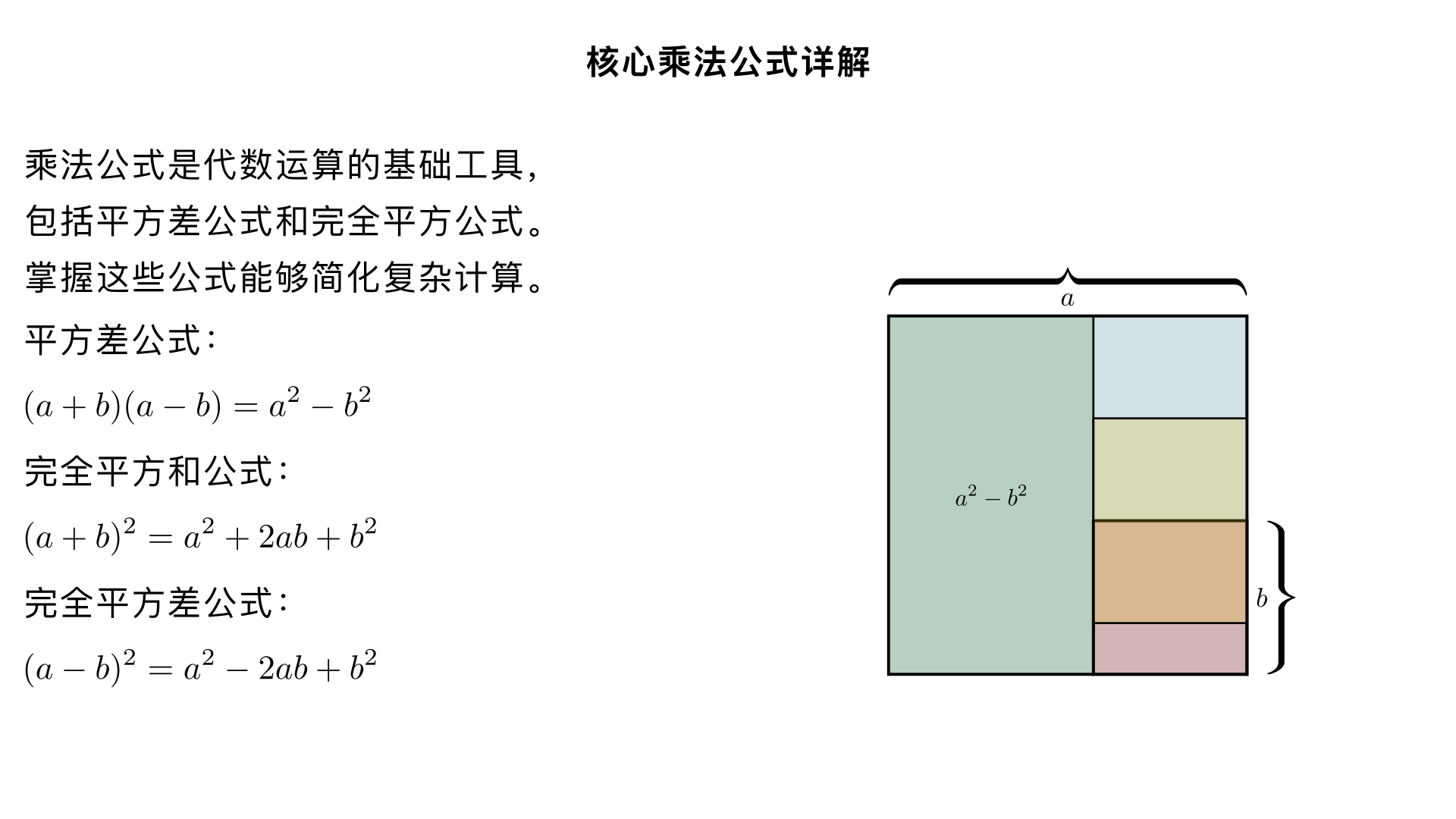
二、核心乘法公式详解 1. 平方差公式 标准形式: (a+b)(a−b)=a 2 −b 2 语言描述:两数和与这两数差的积,等于这两数的平方差 推导过程(多项式乘法展开): (a+b)(a−b) =a⋅a+a⋅(−b)+b⋅a+b⋅(−b) =a 2 −ab+ab−b 2 =a 2 −b 2 结构特点: 左边:两个二项式相乘,其中一项完全相同( a ),另一项互为相反数( b 与 −b ) 右边:相同项的平方减去相反项的平方(同方减反方) 几何意义:边长为 a 的正方形中挖去边长为 b 的小正方形,剩余部分面积为 a 2 −b 2 ,可拼成一个长 (a+b) 、宽 (a−b) 的矩形 2. 完全平方公式(和与差) 完全平方和公式: 标准形式: (a+b) 2 =a 2 +2ab+b 2 语言描述:两数和的平方,等于它们的平方和加上它们积的 2 倍 完全平方差公式: 标准形式: (a−b) 2 =a 2 −2ab+b 2 语言描述:两数差的平方,等于它们的平方和减去它们积的 2 倍 推导过程(以和为例): (a+b) 2 =(a+b)(a+b) =a⋅a+a⋅b+b⋅a+b⋅b =a 2 +2ab+b 2 结构特点(口诀:首平方,尾平方,积的 2 倍在中央): 左边:二项式的平方(两个相同二项式相乘) 右边:三项式,包含首项平方( a 2 )、尾项平方( b 2 )、中间交叉项的 2 倍( ±2ab ),符号与左边二项式中间符号相同 几何意义(以和为例):边长为 a+b 的正方形,可分为边长为 a 的正方形、边长为 b 的正方形,以及两个长 a 宽 b 的矩形,面积和为 a 2 +2ab+b 2 三、公式的灵活应用 1. 基本应用:直接套用公式 平方差公式示例: (x+3)(x−3)=x 2 −3 2 =x 2 −9 (2a+5b)(2a−5b)=(2a) 2 −(5b) 2 =4a 2 −25b 2 完全平方公式示例: (m+4) 2 =m 2 +2⋅m⋅4+4 2 =m 2 +8m+16 (3x−2y) 2 =(3x) 2 −2⋅3x⋅2y+(2y) 2 =9x 2 −12xy+4y 2

▶
二、核心乘法公式详解 1. 平方差公式 标准形式: (a+b)(a−b)=a 2 −b 2 语言描述:两数和与这两数差的积,等于这两数的平方差 推导过程(多项式乘法展开): (a+b)(a−b) =a⋅a+a⋅(−b)+b⋅a+b⋅(−b) =a 2 −ab+ab−b 2 =a 2 −b 2 结构特点: 左边:两个二项式相乘,其中一项完全相同( a ),另一项互为相反数( b 与 −b ) 右边:相同项的平方减去相反项的平方(同方减反方) 几何意义:边长为 a 的正方形中挖去边长为 b 的小正方形,剩余部分面积为 a 2 −b 2 ,可拼成一个长 (a+b) 、宽 (a−b) 的矩形 2. 完全平方公式(和与差) 完全平方和公式: 标准形式: (a+b) 2 =a 2 +2ab+b 2 语言描述:两数和的平方,等于它们的平方和加上它们积的 2 倍 完全平方差公式: 标准形式: (a−b) 2 =a 2 −2ab+b 2 语言描述:两数差的平方,等于它们的平方和减去它们积的 2 倍 推导过程(以和为例): (a+b) 2 =(a+b)(a+b) =a⋅a+a⋅b+b⋅a+b⋅b =a 2 +2ab+b 2 结构特点(口诀:首平方,尾平方,积的 2 倍在中央): 左边:二项式的平方(两个相同二项式相乘) 右边:三项式,包含首项平方( a 2 )、尾项平方( b 2 )、中间交叉项的 2 倍( ±2ab ),符号与左边二项式中间符号相同 几何意义(以和为例):边长为 a+b 的正方形,可分为边长为 a 的正方形、边长为 b 的正方形,以及两个长 a 宽 b 的矩形,面积和为 a 2 +2ab+b 2 三、公式的灵活应用 1. 基本应用:直接套用公式 平方差公式示例: (x+3)(x−3)=x 2 −3 2 =x 2 −9 (2a+5b)(2a−5b)=(2a) 2 −(5b) 2 =4a 2 −25b 2 完全平方公式示例: (m+4) 2 =m 2 +2⋅m⋅4+4 2 =m 2 +8m+16 (3x−2y) 2 =(3x) 2 −2⋅3x⋅2y+(2y) 2 =9x 2 −12xy+4y 2
▶
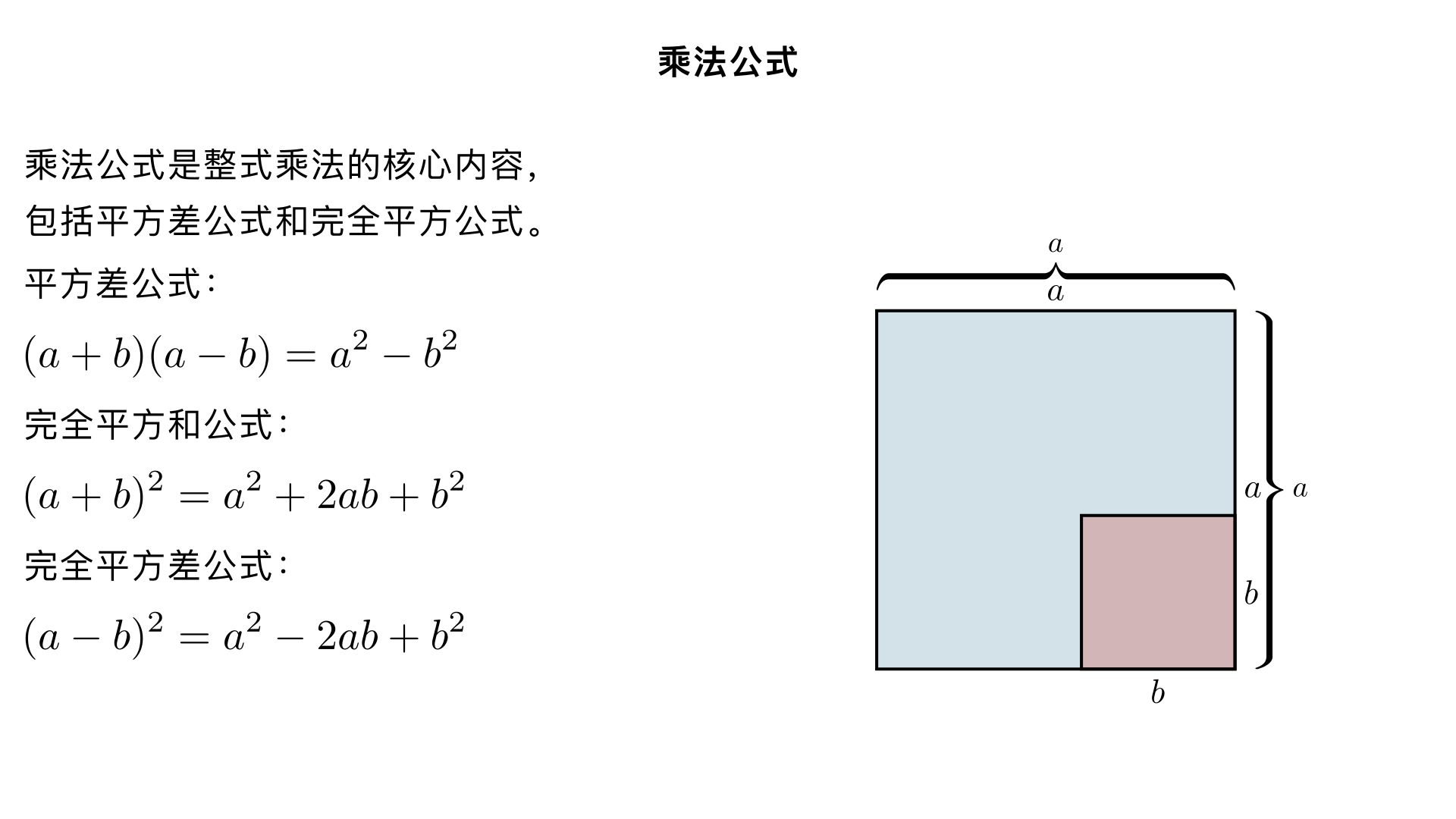
八年级数学 / 整式的乘法 / 乘法公式 乘法公式是整式乘法的核心内容,主要包括平方差公式和完全平方公式,它们是多项式乘法的特殊形式,能大幅简化运算。以下按 “公式 - 推导 - 结构 - 应用 - 题型 - 易错点” 的逻辑系统梳理,方便学习与复习。 一、基础运算回顾(前置知识) 运算类型 公式 语言描述 同底数幂乘法 a m ⋅a n =a m+n 底数不变,指数相加 幂的乘方 (a m ) n =a mn 底数不变,指数相乘 积的乘方 (ab) n =a n b n 积的每个因式分别乘方,再把所得幂相乘 多项式乘法 (a+b)(c+d)=ac+ad+bc+bd 用一个多项式每一项乘另一个多项式每一项,再相加 二、核心乘法公式详解 1. 平方差公式 标准形式: (a+b)(a−b)=a 2 −b 2 语言描述:两数和与这两数差的积,等于这两数的平方差 推导过程(多项式乘法展开): (a+b)(a−b) =a⋅a+a⋅(−b)+b⋅a+b⋅(−b) =a 2 −ab+ab−b 2 =a 2 −b 2 结构特点: 左边:两个二项式相乘,其中一项完全相同( a ),另一项互为相反数( b 与 −b ) 右边:相同项的平方减去相反项的平方(同方减反方) 几何意义:边长为 a 的正方形中挖去边长为 b 的小正方形,剩余部分面积为 a 2 −b 2 ,可拼成一个长 (a+b) 、宽 (a−b) 的矩形 2. 完全平方公式(和与差) 完全平方和公式: 标准形式: (a+b) 2 =a 2 +2ab+b 2 语言描述:两数和的平方,等于它们的平方和加上它们积的 2 倍 完全平方差公式: 标准形式: (a−b) 2 =a 2 −2ab+b 2 语言描述:两数差的平方,等于它们的平方和减去它们积的 2 倍 推导过程(以和为例): (a+b) 2 =(a+b)(a+b) =a⋅a+a⋅b+b⋅a+b⋅b =a 2 +2ab+b 2 结构特点(口诀:首平方,尾平方,积的 2 倍在中央): 左边:二项式的平方(两个相同二项式相乘) 右边:三项式,包含首项平方( a 2 )、尾项平方( b 2 )、中间交叉项的 2 倍( ±2ab ),符号与左边二项式中间符号相同 几何意义(以和为例):边长为 a+b 的正方形,可分为边长为 a 的正方形、边长为 b 的正方形,以及两个长 a 宽 b 的矩形,面积和为 a 2 +2ab+b 2
![八年级数学 / 整式的乘法 / 乘法公式
乘法公式是整式乘法的核心内容,主要包括平方差公式和完全平方公式,它们是多项式乘法的特殊形式,能大幅简化运算。以下按 “公式 - 推导 - 结构 - 应用 - 题型 - 易错点” 的逻辑系统梳理,方便学习与复习。
一、基础运算回顾(前置知识)
运算类型 公式 语言描述
同底数幂乘法
a
m
⋅a
n
=a
m+n
底数不变,指数相加
幂的乘方
(a
m
)
n
=a
mn
底数不变,指数相乘
积的乘方
(ab)
n
=a
n
b
n
积的每个因式分别乘方,再把所得幂相乘
多项式乘法
(a+b)(c+d)=ac+ad+bc+bd
用一个多项式每一项乘另一个多项式每一项,再相加
二、核心乘法公式详解
1. 平方差公式
标准形式:
(a+b)(a−b)=a
2
−b
2
语言描述:两数和与这两数差的积,等于这两数的平方差
推导过程(多项式乘法展开):
(a+b)(a−b)
=a⋅a+a⋅(−b)+b⋅a+b⋅(−b)
=a
2
−ab+ab−b
2
=a
2
−b
2
结构特点:
左边:两个二项式相乘,其中一项完全相同(
a
),另一项互为相反数(
b
与
−b
)
右边:相同项的平方减去相反项的平方(同方减反方)
几何意义:边长为
a
的正方形中挖去边长为
b
的小正方形,剩余部分面积为
a
2
−b
2
,可拼成一个长
(a+b)
、宽
(a−b)
的矩形
2. 完全平方公式(和与差)
完全平方和公式:
标准形式:
(a+b)
2
=a
2
+2ab+b
2
语言描述:两数和的平方,等于它们的平方和加上它们积的 2 倍
完全平方差公式:
标准形式:
(a−b)
2
=a
2
−2ab+b
2
语言描述:两数差的平方,等于它们的平方和减去它们积的 2 倍
推导过程(以和为例):
(a+b)
2
=(a+b)(a+b)
=a⋅a+a⋅b+b⋅a+b⋅b
=a
2
+2ab+b
2
结构特点(口诀:首平方,尾平方,积的 2 倍在中央):
左边:二项式的平方(两个相同二项式相乘)
右边:三项式,包含首项平方(
a
2
)、尾项平方(
b
2
)、中间交叉项的 2 倍(
±2ab
),符号与左边二项式中间符号相同
几何意义(以和为例):边长为
a+b
的正方形,可分为边长为
a
的正方形、边长为
b
的正方形,以及两个长
a
宽
b
的矩形,面积和为
a
2
+2ab+b
2
三、公式的灵活应用
1. 基本应用:直接套用公式
平方差公式示例:
(x+3)(x−3)=x
2
−3
2
=x
2
−9
(2a+5b)(2a−5b)=(2a)
2
−(5b)
2
=4a
2
−25b
2
完全平方公式示例:
(m+4)
2
=m
2
+2⋅m⋅4+4
2
=m
2
+8m+16
(3x−2y)
2
=(3x)
2
−2⋅3x⋅2y+(2y)
2
=9x
2
−12xy+4y
2
2. 变形应用:公式的逆用与拓展
公式变形 表达式 应用场景
平方差逆用
a
2
−b
2
=(a+b)(a−b)
因式分解、简便计算
完全平方逆用
a
2
±2ab+b
2
=(a±b)
2
因式分解、配方
完全平方和差关系
(a+b)
2
−(a−b)
2
=4ab
求
ab
值
平方和公式
a
2
+b
2
=(a+b)
2
−2ab=(a−b)
2
+2ab
知和求平方和、知差求平方和
示例:
若
x+y=5
,
xy=3
,求
x
2
+y
2
x
2
+y
2
=(x+y)
2
−2xy=5
2
−2×3=25−6=19
3. 特殊形式应用(换元思想)
当公式中的
a
、
b
为多项式时,可将其视为一个整体套用公式:
(a+b+c)(a+b−c)=[(a+b)+c][(a+b)−c]=(a+b)
2
−c
2
=a
2
+2ab+b
2
−c
2
(x−y+z)
2
=[(x−y)+z]
2
=(x−y)
2
+2(x−y)z+z
2
=x
2
−2xy+y
2
+2xz−2yz+z
2
4. 简便计算应用
利用公式简化复杂计算:
99×101=(100−1)(100+1)=100
2
−1
2
=10000−1=9999
102
2
=(100+2)
2
=100
2
+2×100×2+2
2
=10000+400+4=10404
99
2
=(100−1)
2
=100
2
−2×100×1+1
2
=10000−200+1=9801
四、常见题型分类解析
题型 解题关键 示例
公式直接计算 识别公式结构,找准
a
、
b
(−2m−3n)
2
=(2m+3n)
2
=4m
2
+12mn+9n
2
公式逆用(因式分解) 识别平方差或完全平方式
x
2
−6x+9=(x−3)
2
条件求值 利用公式变形,整体代入 已知
a−b=3
,求
a
2
+b
2
−6ab
(变形为
(a−b)
2
−4ab
)
配方求最值 配成完全平方式,利用平方非负性 求
x
2
−4x+5
最小值(配方为
(x−2)
2
+1
,最小值 1)
化简求值 先化简再代入,避免繁琐计算 化简
(2x+1)
2
−(2x−1)
2
,再代入
x=
4
1
五、易错点警示与避错技巧
易错点 错误示例 正确做法
完全平方漏中间项
(a+b)
2
=a
2
+b
2
牢记 “首平方,尾平方,积的 2 倍在中央”,中间项为
2ab
完全平方符号错误
(a−b)
2
=a
2
−2ab−b
2
尾项平方恒为正,应为
a
2
−2ab+b
2
平方差公式误用
(a+b)(c−d)=a
2
−b
2
必须满足 “一项同,一项反”,不同则用多项式乘法
系数未平方
(2a)
2
=2a
2
系数与字母都要平方,应为
4a
2
符号处理错误
(−a−b)
2
=a
2
−2ab+b
2
提取负号再平方:
(−a−b)
2
=(a+b)
2
=a
2
+2ab+b
2
避错口诀:
平方差:同方减反方,符号要对好
完全平方:和平方加两倍,差平方减两倍,尾项平方永为正
遇负号:先定号,再平方,避免符号乱
六、思维拓展:拓展乘法公式(选学)
三数和平方公式:
(a+b+c)
2
=a
2
+b
2
+c
2
+2ab+2ac+2bc
立方和公式:
(a+b)(a
2
−ab+b
2
)=a
3
+b
3
立方差公式:
(a−b)(a
2
+ab+b
2
)=a
3
−b
3
总结
乘法公式是代数运算的基础工具,核心在于理解公式的结构特征与推导本质,而非死记硬背。通过大量练习掌握直接应用、逆用与变形应用,同时警惕常见易错点,就能熟练运用公式解决各类问题,为后续因式分解、二次函数等学习打下坚实基础。](https://manimvideo.explanation.fun/video/cover/595653712674344960.png)
▶
八年级数学 / 整式的乘法 / 乘法公式 乘法公式是整式乘法的核心内容,主要包括平方差公式和完全平方公式,它们是多项式乘法的特殊形式,能大幅简化运算。以下按 “公式 - 推导 - 结构 - 应用 - 题型 - 易错点” 的逻辑系统梳理,方便学习与复习。 一、基础运算回顾(前置知识) 运算类型 公式 语言描述 同底数幂乘法 a m ⋅a n =a m+n 底数不变,指数相加 幂的乘方 (a m ) n =a mn 底数不变,指数相乘 积的乘方 (ab) n =a n b n 积的每个因式分别乘方,再把所得幂相乘 多项式乘法 (a+b)(c+d)=ac+ad+bc+bd 用一个多项式每一项乘另一个多项式每一项,再相加 二、核心乘法公式详解 1. 平方差公式 标准形式: (a+b)(a−b)=a 2 −b 2 语言描述:两数和与这两数差的积,等于这两数的平方差 推导过程(多项式乘法展开): (a+b)(a−b) =a⋅a+a⋅(−b)+b⋅a+b⋅(−b) =a 2 −ab+ab−b 2 =a 2 −b 2 结构特点: 左边:两个二项式相乘,其中一项完全相同( a ),另一项互为相反数( b 与 −b ) 右边:相同项的平方减去相反项的平方(同方减反方) 几何意义:边长为 a 的正方形中挖去边长为 b 的小正方形,剩余部分面积为 a 2 −b 2 ,可拼成一个长 (a+b) 、宽 (a−b) 的矩形 2. 完全平方公式(和与差) 完全平方和公式: 标准形式: (a+b) 2 =a 2 +2ab+b 2 语言描述:两数和的平方,等于它们的平方和加上它们积的 2 倍 完全平方差公式: 标准形式: (a−b) 2 =a 2 −2ab+b 2 语言描述:两数差的平方,等于它们的平方和减去它们积的 2 倍 推导过程(以和为例): (a+b) 2 =(a+b)(a+b) =a⋅a+a⋅b+b⋅a+b⋅b =a 2 +2ab+b 2 结构特点(口诀:首平方,尾平方,积的 2 倍在中央): 左边:二项式的平方(两个相同二项式相乘) 右边:三项式,包含首项平方( a 2 )、尾项平方( b 2 )、中间交叉项的 2 倍( ±2ab ),符号与左边二项式中间符号相同 几何意义(以和为例):边长为 a+b 的正方形,可分为边长为 a 的正方形、边长为 b 的正方形,以及两个长 a 宽 b 的矩形,面积和为 a 2 +2ab+b 2 三、公式的灵活应用 1. 基本应用:直接套用公式 平方差公式示例: (x+3)(x−3)=x 2 −3 2 =x 2 −9 (2a+5b)(2a−5b)=(2a) 2 −(5b) 2 =4a 2 −25b 2 完全平方公式示例: (m+4) 2 =m 2 +2⋅m⋅4+4 2 =m 2 +8m+16 (3x−2y) 2 =(3x) 2 −2⋅3x⋅2y+(2y) 2 =9x 2 −12xy+4y 2 2. 变形应用:公式的逆用与拓展 公式变形 表达式 应用场景 平方差逆用 a 2 −b 2 =(a+b)(a−b) 因式分解、简便计算 完全平方逆用 a 2 ±2ab+b 2 =(a±b) 2 因式分解、配方 完全平方和差关系 (a+b) 2 −(a−b) 2 =4ab 求 ab 值 平方和公式 a 2 +b 2 =(a+b) 2 −2ab=(a−b) 2 +2ab 知和求平方和、知差求平方和 示例: 若 x+y=5 , xy=3 ,求 x 2 +y 2 x 2 +y 2 =(x+y) 2 −2xy=5 2 −2×3=25−6=19 3. 特殊形式应用(换元思想) 当公式中的 a 、 b 为多项式时,可将其视为一个整体套用公式: (a+b+c)(a+b−c)=[(a+b)+c][(a+b)−c]=(a+b) 2 −c 2 =a 2 +2ab+b 2 −c 2 (x−y+z) 2 =[(x−y)+z] 2 =(x−y) 2 +2(x−y)z+z 2 =x 2 −2xy+y 2 +2xz−2yz+z 2 4. 简便计算应用 利用公式简化复杂计算: 99×101=(100−1)(100+1)=100 2 −1 2 =10000−1=9999 102 2 =(100+2) 2 =100 2 +2×100×2+2 2 =10000+400+4=10404 99 2 =(100−1) 2 =100 2 −2×100×1+1 2 =10000−200+1=9801 四、常见题型分类解析 题型 解题关键 示例 公式直接计算 识别公式结构,找准 a 、 b (−2m−3n) 2 =(2m+3n) 2 =4m 2 +12mn+9n 2 公式逆用(因式分解) 识别平方差或完全平方式 x 2 −6x+9=(x−3) 2 条件求值 利用公式变形,整体代入 已知 a−b=3 ,求 a 2 +b 2 −6ab (变形为 (a−b) 2 −4ab ) 配方求最值 配成完全平方式,利用平方非负性 求 x 2 −4x+5 最小值(配方为 (x−2) 2 +1 ,最小值 1) 化简求值 先化简再代入,避免繁琐计算 化简 (2x+1) 2 −(2x−1) 2 ,再代入 x= 4 1 五、易错点警示与避错技巧 易错点 错误示例 正确做法 完全平方漏中间项 (a+b) 2 =a 2 +b 2 牢记 “首平方,尾平方,积的 2 倍在中央”,中间项为 2ab 完全平方符号错误 (a−b) 2 =a 2 −2ab−b 2 尾项平方恒为正,应为 a 2 −2ab+b 2 平方差公式误用 (a+b)(c−d)=a 2 −b 2 必须满足 “一项同,一项反”,不同则用多项式乘法 系数未平方 (2a) 2 =2a 2 系数与字母都要平方,应为 4a 2 符号处理错误 (−a−b) 2 =a 2 −2ab+b 2 提取负号再平方: (−a−b) 2 =(a+b) 2 =a 2 +2ab+b 2 避错口诀: 平方差:同方减反方,符号要对好 完全平方:和平方加两倍,差平方减两倍,尾项平方永为正 遇负号:先定号,再平方,避免符号乱 六、思维拓展:拓展乘法公式(选学) 三数和平方公式: (a+b+c) 2 =a 2 +b 2 +c 2 +2ab+2ac+2bc 立方和公式: (a+b)(a 2 −ab+b 2 )=a 3 +b 3 立方差公式: (a−b)(a 2 +ab+b 2 )=a 3 −b 3 总结 乘法公式是代数运算的基础工具,核心在于理解公式的结构特征与推导本质,而非死记硬背。通过大量练习掌握直接应用、逆用与变形应用,同时警惕常见易错点,就能熟练运用公式解决各类问题,为后续因式分解、二次函数等学习打下坚实基础。
![八年级数学 / 整式的乘法 / 整式的乘法
核心总览:整式乘法分为三大基础类型(单项式 × 单项式、单项式 × 多项式、多项式 × 多项式),以幂的运算法则为基础,延伸出平方差公式与完全平方公式两大常用乘法公式,运算时需注意符号与不漏项两大关键。
一、基础准备:幂的运算法则(必备前置知识)
法则 公式 示例 注意事项
同底数幂相乘
a
m
⋅a
n
=a
m+n
(
m,n
为正整数)
x
3
⋅x
5
=x
8
底数必须相同,指数相加
幂的乘方
(a
m
)
n
=a
mn
(y
2
)
4
=y
8
底数不变,指数相乘
积的乘方
(ab)
n
=a
n
b
n
(2x)
3
=8x
3
积中每个因式分别乘方
二、单项式与单项式相乘(整式乘法基础)
1. 运算法则
三步骤法:
系数相乘:按有理数乘法计算
同底数幂相乘:底数不变,指数相加
单独字母保留:只在一个单项式中出现的字母,连同指数作为积的因式
2. 典型例题
例 1:计算
2a
2
b⋅(−3ab
3
)
解:
(2×−3)⋅(a
2
⋅a)⋅(b⋅b
3
)=−6a
3
b
4
例 2:计算
(−2x
2
y)
3
⋅3xy
2
解:先算积的乘方:
(−2)
3
⋅(x
2
)
3
⋅y
3
=−8x
6
y
3
再相乘:
−8x
6
y
3
⋅3xy
2
=−24x
7
y
5
三、单项式与多项式相乘(转化思想的应用)
1. 运算法则
乘法分配律推广:用单项式乘多项式的每一项,再把所得的积相加公式:
m(a+b+c)=ma+mb+mc
2. 典型例题
例 3:计算
−2x(3x
2
−4x+1)
解:
−2x⋅3x
2
+(−2x)⋅(−4x)+(−2x)⋅1=−6x
3
+8x
2
−2x
3. 易错警示
符号问题:单项式为负时,每一项相乘都要变号
积的项数:结果项数与原多项式项数相同,防止漏乘
指数计算:单项式与多项式中同字母相乘时,指数相加而非相乘
四、多项式与多项式相乘(基础乘法的核心)
1. 运算法则
分步相乘再合并:先用一个多项式的每一项乘另一个多项式的每一项,再把所得积合并同类项公式:
(a+b)(m+n)=am+an+bm+bn
2. 典型例题
例 4:计算
(x+2)(2x−3)
解:
x⋅2x+x⋅(−3)+2⋅2x+2⋅(−3)
=2x
2
−3x+4x−6
=2x
2
+x−6
(合并同类项)
3. 常用技巧
网格法:将两个多项式的项写在网格的行与列,交叉相乘后求和
“首首末末” 法:先乘首尾项,再乘交叉项,最后合并
五、乘法公式(多项式乘法的特例,需熟练掌握)
1. 平方差公式
公式:
(a+b)(a−b)=a
2
−b
2
特点:两数和乘以两数差,结果为两数的平方差
例 5:
(3x+2)(3x−2)=(3x)
2
−2
2
=9x
2
−4
2. 完全平方公式
和的平方:
(a+b)
2
=a
2
+2ab+b
2
差的平方:
(a−b)
2
=a
2
−2ab+b
2
口诀:首平方,尾平方,积的 2 倍在中央,符号看中间
例 6:
(2x−5)
2
=(2x)
2
−2⋅2x⋅5+5
2
=4x
2
−20x+25
3. 公式应用注意事项
公式中的
a,b
可以是数字、字母或单项式 / 多项式
例:
(x+y+z)(x+y−z)=[(x+y)+z][(x+y)−z]=(x+y)
2
−z
2
(整体思想)
避免常见错误:
(a+b)
2
=a
2
+b
2
(漏掉中间的
2ab
)
(a−b)
2
=a
2
−b
2
(应为
a
2
−2ab+b
2
)
六、综合运算步骤与易错点汇总
1. 通用运算步骤
先算乘方(幂的运算),再算乘法,最后算加减(合并同类项)
有括号先算括号内,多重括号从内到外
能用乘法公式的优先使用公式简化计算](https://manimvideo.explanation.fun/video/cover/595293059794583553.png)
▶
八年级数学 / 整式的乘法 / 整式的乘法 核心总览:整式乘法分为三大基础类型(单项式 × 单项式、单项式 × 多项式、多项式 × 多项式),以幂的运算法则为基础,延伸出平方差公式与完全平方公式两大常用乘法公式,运算时需注意符号与不漏项两大关键。 一、基础准备:幂的运算法则(必备前置知识) 法则 公式 示例 注意事项 同底数幂相乘 a m ⋅a n =a m+n ( m,n 为正整数) x 3 ⋅x 5 =x 8 底数必须相同,指数相加 幂的乘方 (a m ) n =a mn (y 2 ) 4 =y 8 底数不变,指数相乘 积的乘方 (ab) n =a n b n (2x) 3 =8x 3 积中每个因式分别乘方 二、单项式与单项式相乘(整式乘法基础) 1. 运算法则 三步骤法: 系数相乘:按有理数乘法计算 同底数幂相乘:底数不变,指数相加 单独字母保留:只在一个单项式中出现的字母,连同指数作为积的因式 2. 典型例题 例 1:计算 2a 2 b⋅(−3ab 3 ) 解: (2×−3)⋅(a 2 ⋅a)⋅(b⋅b 3 )=−6a 3 b 4 例 2:计算 (−2x 2 y) 3 ⋅3xy 2 解:先算积的乘方: (−2) 3 ⋅(x 2 ) 3 ⋅y 3 =−8x 6 y 3 再相乘: −8x 6 y 3 ⋅3xy 2 =−24x 7 y 5 三、单项式与多项式相乘(转化思想的应用) 1. 运算法则 乘法分配律推广:用单项式乘多项式的每一项,再把所得的积相加公式: m(a+b+c)=ma+mb+mc 2. 典型例题 例 3:计算 −2x(3x 2 −4x+1) 解: −2x⋅3x 2 +(−2x)⋅(−4x)+(−2x)⋅1=−6x 3 +8x 2 −2x 3. 易错警示 符号问题:单项式为负时,每一项相乘都要变号 积的项数:结果项数与原多项式项数相同,防止漏乘 指数计算:单项式与多项式中同字母相乘时,指数相加而非相乘 四、多项式与多项式相乘(基础乘法的核心) 1. 运算法则 分步相乘再合并:先用一个多项式的每一项乘另一个多项式的每一项,再把所得积合并同类项公式: (a+b)(m+n)=am+an+bm+bn 2. 典型例题 例 4:计算 (x+2)(2x−3) 解: x⋅2x+x⋅(−3)+2⋅2x+2⋅(−3) =2x 2 −3x+4x−6 =2x 2 +x−6 (合并同类项) 3. 常用技巧 网格法:将两个多项式的项写在网格的行与列,交叉相乘后求和 “首首末末” 法:先乘首尾项,再乘交叉项,最后合并 五、乘法公式(多项式乘法的特例,需熟练掌握) 1. 平方差公式 公式: (a+b)(a−b)=a 2 −b 2 特点:两数和乘以两数差,结果为两数的平方差 例 5: (3x+2)(3x−2)=(3x) 2 −2 2 =9x 2 −4 2. 完全平方公式 和的平方: (a+b) 2 =a 2 +2ab+b 2 差的平方: (a−b) 2 =a 2 −2ab+b 2 口诀:首平方,尾平方,积的 2 倍在中央,符号看中间 例 6: (2x−5) 2 =(2x) 2 −2⋅2x⋅5+5 2 =4x 2 −20x+25 3. 公式应用注意事项 公式中的 a,b 可以是数字、字母或单项式 / 多项式 例: (x+y+z)(x+y−z)=[(x+y)+z][(x+y)−z]=(x+y) 2 −z 2 (整体思想) 避免常见错误: (a+b) 2 =a 2 +b 2 (漏掉中间的 2ab ) (a−b) 2 =a 2 −b 2 (应为 a 2 −2ab+b 2 ) 六、综合运算步骤与易错点汇总 1. 通用运算步骤 先算乘方(幂的运算),再算乘法,最后算加减(合并同类项) 有括号先算括号内,多重括号从内到外 能用乘法公式的优先使用公式简化计算
▶