T
Teach Me AnythingTMA
Video History
Page 5 / 47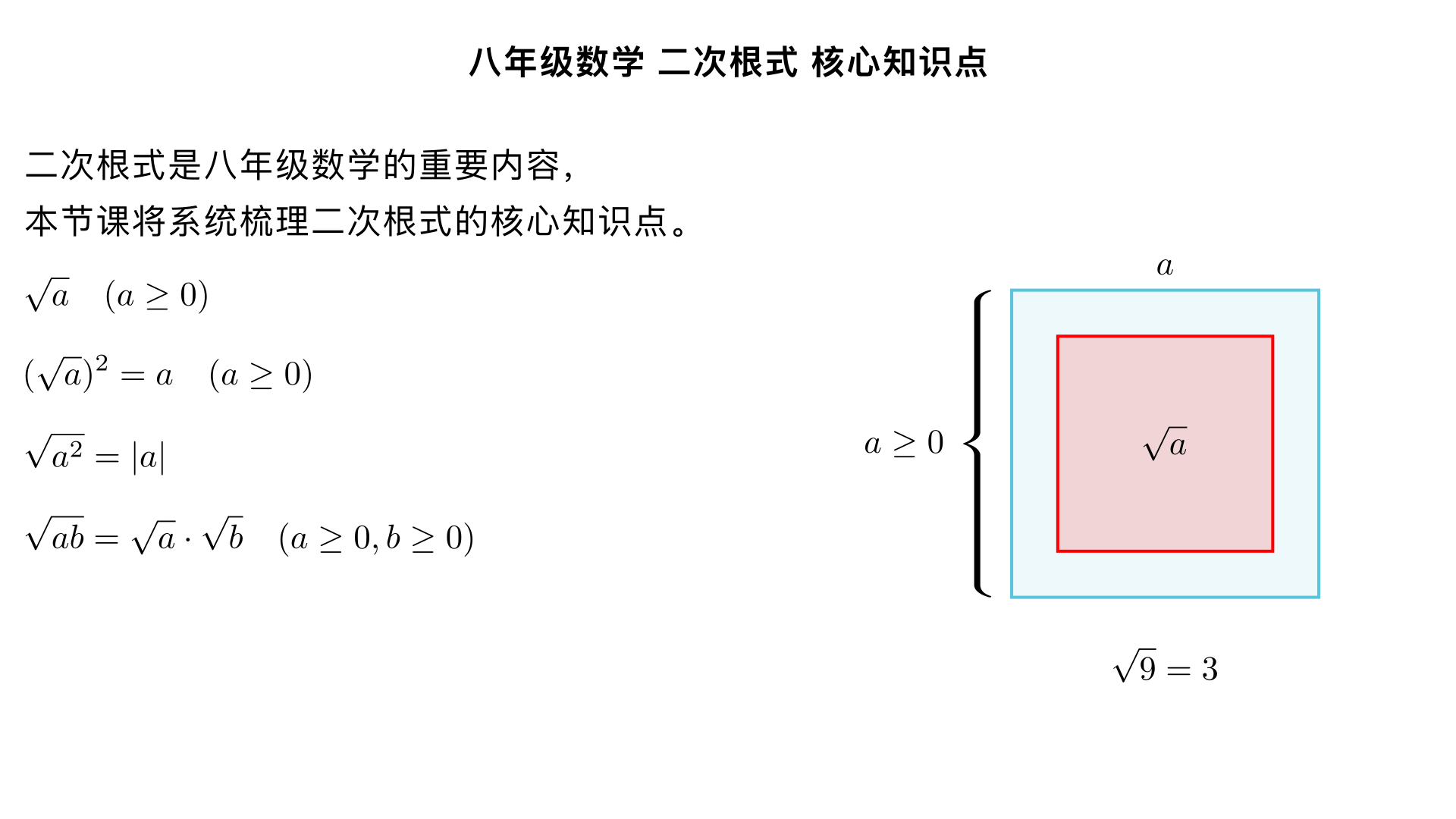
▶
八年级数学 二次根式 核心知识点(体系化梳理) 本部分是二次根式的入门核心,围绕定义、双重非负性、基本性质、最简二次根式展开,是后续二次根式运算的基础,也是八年级同步课程的核心考点,内容由浅入深、贴合课堂进度。 一、二次根式的定义 一般地,我们把形如 a (a≥0) 的式子叫做二次根式。 关键解读 根指数为2(二次根式的根指数 2 通常省略不写,注意与三次根式 3 a 区分); 形式上必须包含二次根号 ; 被开方数 a 的取值是核心: a≥0 (这是二次根式有意义的前提)。 举例 是二次根式: 2 、 x+1 (x≥−1) 、 0 (被开方数均非负); 不是二次根式: −3 (被开方数为负)、 3 4 (根指数为 3)、 2 a (注意: 2 a 是二次根式的倍数形式,属于二次根式,此为易混点)。 二、二次根式的双重非负性(核心考点) 二次根式 a (a≥0) 本身具有双重非负性,是八年级填空、选择的高频考点,必须熟记: 被开方数非负: a≥0 ; 二次根式本身的值非负: a ≥0 。 典型应用:求字母取值 / 代数式的值 例:若 x−2 + y+3 =0 ,求 x+y 的值。解:∵ x−2 ≥0 , y+3 ≥0 ,两个非负数的和为 0,则各自为 0∴ x−2=0 , y+3=0 → x=2 , y=−3 → x+y=−1 。 三、二次根式有意义的条件(定义延伸) 求二次根式中字母的取值范围,只需紧扣被开方数非负;若二次根式出现在分母中,需额外满足分母不为 0(双重条件)。 分类例题 单二次根式:求 3x−6 有意义的 x 的取值范围 解: 3x−6≥0 → x≥2 。 二次根式在分母:求 2−x 1 有意义的 x 的取值范围 解: { 2−x≥0 2−x =0 → 2−x>0 → x<2 。 多个二次根式组合:求 x−1 + 3−x 有意义的 x 的取值范围 解: { x−1≥0 3−x≥0 → 1≤x≤3 。 四、二次根式的基本性质(化简、运算的基础) 以下性质均为八年级阶段核心,需结合取值范围熟记,切勿忽略条件: 性质公式 适用条件 文字解读 举例 ( a ) 2 =a a≥0 非负数的算术平方根的平方,等于它本身 ( 5 ) 2 =5 , ( x−2 ) 2 =x−2(x≥2) $\sqrt{a^2} = a = \begin{cases}a & (a\geq0) \ -a & (a<0)\end{cases}$ a 为任意实数 一个数的平方的算术平方根,等于这个数的绝对值 $\sqrt{(-3)^2}= -3 =3 , \sqrt{7^2}=7 , \sqrt{(x-1)^2}= x-1 $ ab = a ⋅ b a≥0 , b≥0 积的算术平方根,等于算术平方根的积 12 = 4×3 = 4 × 3 =2 3 b a = b a a≥0 , b>0 商的算术平方根,等于算术平方根的商 9 2 = 9 2 = 3 2 易错点提醒 ( a ) 2 和 a 2 的区别:前者被开方数 a≥0 ,结果就是 a ;后者 a 为任意数,结果是 ∣a∣ (八年级最易出错的性质); 积 / 商的性质中, b 的取值:乘法中 b≥0 ,除法中 b>0 (分母不能为 0)。 五、最简二次根式(化简的最终目标) 二次根式的化简、加减运算均需先化为最简二次根式,定义为满足以下两个条件的二次根式: 被开方数中不含分母; 被开方数中不含能开得尽方的因数或因式(即被开方数的因数都是质数,因式都是最简整式)。 举例 最简二次根式: 2 、 3 5 、 x+1 (x≥−1) (满足两个条件); 非最简二次根式: 8 (含能开方的因数 4)、 3 1 (含分母)、 12x 2 (x≥0) (含能开方的因式 x 2 )。 二次根式化简的基本步骤 去分母:利用商的性质,将分母中的根号化去(八年级阶段主要是分母为单个二次根式的情况,如 2 1 = 2 2 ); 开方因数 / 因式:将被开方数中能开得尽方的因数 / 因式开方后移到根号外,如 18 = 9×2 =3 2 , 27x 3 =3x 3x (x≥0) 。
▶
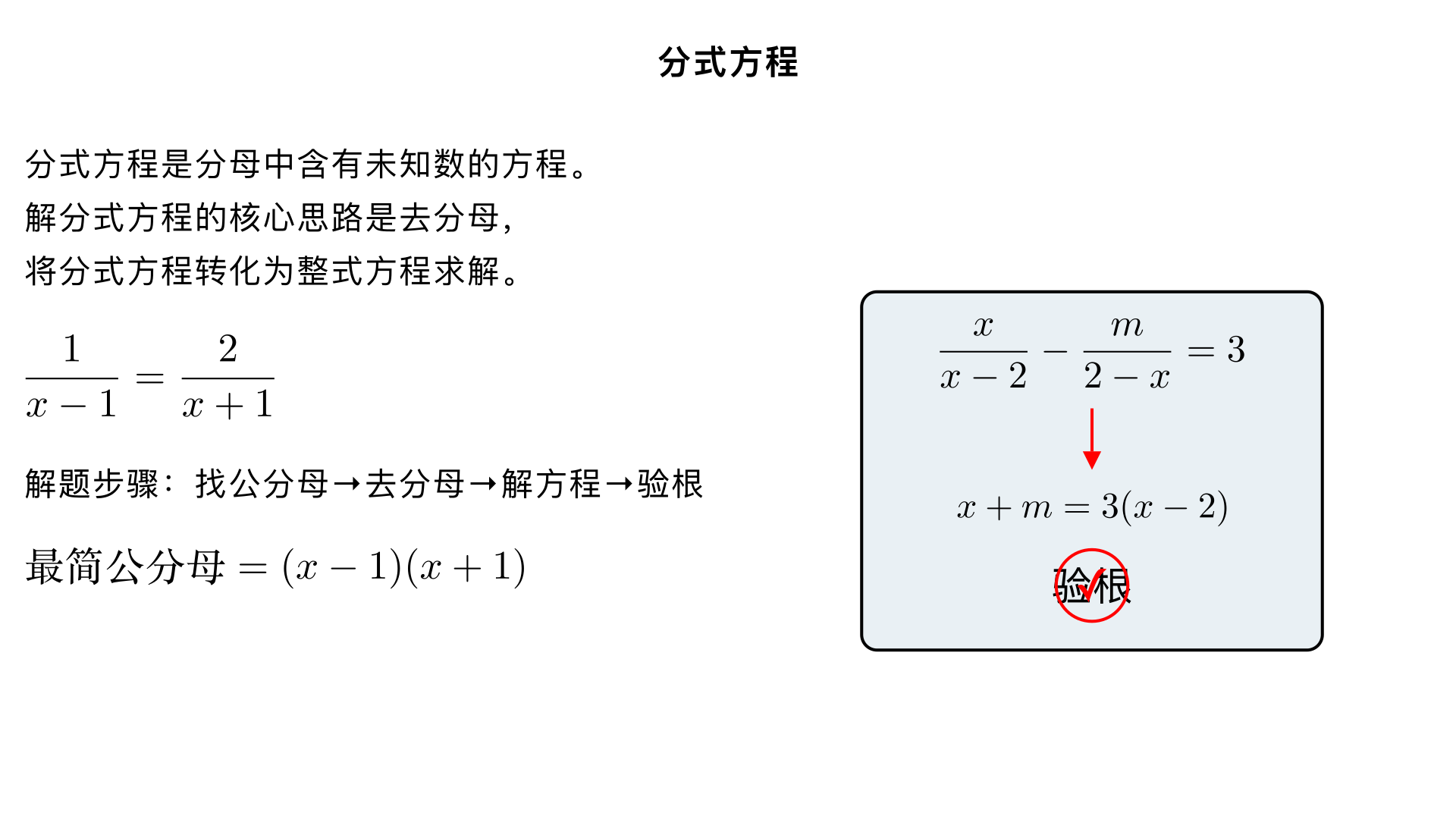
八年级数学 / 分式 / 分式方程 本章节核心围绕分式方程的定义、解法、验根展开,核心思想是转化思想(将分式方程化为已学的整式方程求解),同时重点掌握分式方程的实际应用,是八年级分式板块的重点和中考基础考点,以下为系统化知识点梳理 + 解题方法 + 易错点总结。 一、分式方程的定义 分母中含有未知数的方程叫做分式方程。✅ 核心判定依据:①是方程(含等号);②分母含有未知数(分母是常数的不是分式方程)。❌ 注意区分整式方程与分式方程: 整式方程 分式方程 分母仅为常数 分母含未知数 例: 2 x+1 =3 、 2x−5=0 例: x 1 =2 、 x−1 x = x+3 2 二、解分式方程的核心思路与步骤 1. 核心思路 去分母,把分式方程转化为整式方程(一元一次方程为主,八年级阶段),利用整式方程的解法求解,最后验根(关键步骤,不可省略)。 2. 具体解题步骤(五步走,记牢!) 以解方程 x−1 1 = x+1 2 为例演示: 步骤 1:找最简公分母 先观察所有分母的因式,取各分母所有因式的最高次幂的积作为最简公分母;若分母有多项式,先因式分解再找。例:分母为 x−1 和 x+1 ,最简公分母为 (x−1)(x+1) 。 步骤 2:去分母,化整式方程 方程两边同时乘最简公分母,消去分母,注意:不要漏乘不含分母的项(若方程有常数项,常数项也要乘公分母)。例:两边同乘 (x−1)(x+1) ,得: x+1=2(x−1) 。 步骤 3:解转化后的整式方程 按一元一次方程的解法(去括号、移项、合并同类项、系数化为 1)求解。例: x+1=2x−2 → 移项得 1+2=2x−x → x=3 。 步骤 4:验根(分式方程的专属步骤,必考易错点) (1)为什么要验根? 去分母时,方程两边乘了含未知数的整式(最简公分母),若该整式的值为 0,会违反 “等式两边同时乘非 0 数,等式仍成立” 的性质,此时会产生增根,增根本质不是原分式方程的解,只是转化后整式方程的解。 (2)验根的两种方法(方法 2 更简便,优先用) 方法 1:代入原分式方程,检查①分母是否为 0;②左右两边是否相等。 方法 2:代入最简公分母,若公分母 = 0 → 是增根,舍去;若公分母≠0 → 是原方程的解。 例:把 x=3 代入 (x−1)(x+1) ,得 2×4=8 =0 ,故 x=3 是原方程的解。 步骤 5:写出最终解 若有解直接写,若无解(仅含增根)需注明 “原分式方程无解”。 三、增根的核心知识点 1. 增根的定义 使原分式方程的分母为 0的根(同时是转化后整式方程的根),增根不是原分式方程的解。 2. 常考题型:已知分式方程有增根,求参数的值 解题三步法(核心:先找增根,再代整式方程): 令最简公分母 = 0,求出所有可能的增根; 把分式方程化为整式方程(不含分母); 将增根代入整式方程,解出参数的值。 例题:若方程 x−2 x − 2−x m =3 有增根,求 m 的值。解:① 令最简公分母 x−2=0 ,得增根 x=2 ;② 去分母: x+m=3(x−2) (注意: 2−x=−(x−2) ,符号易出错);③ 把 x=2 代入整式方程: 2+m=3×0 → m=−2 。 四、分式方程的实际应用(重点 + 难点) 分式方程的应用与一元一次方程应用的解题思路一致,仅多一步双重验根,是八年级期末、中考的常考应用题类型(行程、工程、销售、配套问题为主)。 1. 解题六步骤 审→设→列→解→验→答 审:审清题意,找出等量关系(核心,找题中表示相等的语句); 设:设未知数(直接设:求什么设什么;间接设:设中间量,简化列式); 列:根据等量关系,列出分式方程; 解:按分式方程的解法解出未知数; 验:双重验根(①检验是否为增根;②检验是否符合实际意义,如人数、天数、速度不能为负,数量为正整数等); 答:写出答案(带单位)。 2. 常见应用类型及等量关系 八年级高频考 3 类,记牢核心公式和等量关系: (1)工程问题 核心公式: 工 作 总 量 工 作 效 率 工 作 时 间 , 工 作 效 率 工 作 总 量 工 作 时 间 ✅ 常用技巧:若无明确工作总量,设工作总量为 1(如 “完成一项工程”“加工一批零件”)。等量关系:合作效率 = 各效率之和、甲工作量 + 乙工作量 = 总工作量。 (2)行程问题 核心公式: 路 程 速 度 时 间 , 速 度 路 程 时 间 , 时 间 路 程 速 度 ✅ 高频考:顺水 / 逆水行船、相遇 / 追及、路程相同的快慢行。补充:顺水速度 = 静水速度 + 水流速度,逆水速度 = 静水速度 - 水流速度。 (3)销售 / 比例问题 核心:单价、数量、总价的关系( 总 价 单 价 数 量 ),或 “倍数 / 比例” 等量关系(如 “甲的速度是乙的 1.5 倍”)。 3. 应用例题(工程问题,贴合八年级难度) 例题:为美化校园,某校需清理一块草坪,若单独由七年级完成需 15 天,单独由八年级完成需 10 天。现七年级先做 3 天,剩下的由七、八年级合作完成,还需多少天?解:① 审:工作总量 = 1,七年级效率 15 1 ,八年级效率 10 1 ,七年级先做 3 天 + 合作天数 = 总天数;② 设:设还需 x 天完成;③ 列:七年级先做的工作量 + 合作工作量 = 1 → 15 3 +( 15 1 + 10 1 )x=1 ;④ 解:去分母(公分母 30)→ 6+(2+3)x=30 → 5x=24 → x=4.8 ;⑤ 验: x=4.8 是分式方程的解,且天数为正,符合实际;⑥ 答:还需 4.8 天完成。 五、解分式方程的常见易错点(避坑指南) 八年级学生最易在以下 5 点丢分,解题时逐一检查: 去分母漏乘不含分母的项:如方程 x 1 +2=3 ,两边乘 x 易写成 1+2=3x (正确: 1+2x=3x ); 分母变号出错:如 2−x 1 =− x−2 1 ,去分母时忽略符号,导致整式方程列错; 忘记验根:解完直接写答案,增根未舍去(阅卷时直接扣分); 找最简公分母未因式分解:如分母 x 2 −1 和 x+1 ,未分解 x 2 −1=(x−1)(x+1) ,错把公分母写成 x 2 −1(x+1) ; 实际应用未双重验根:解出负数或小数(如人数),未舍去,不符合实际意义。
▶
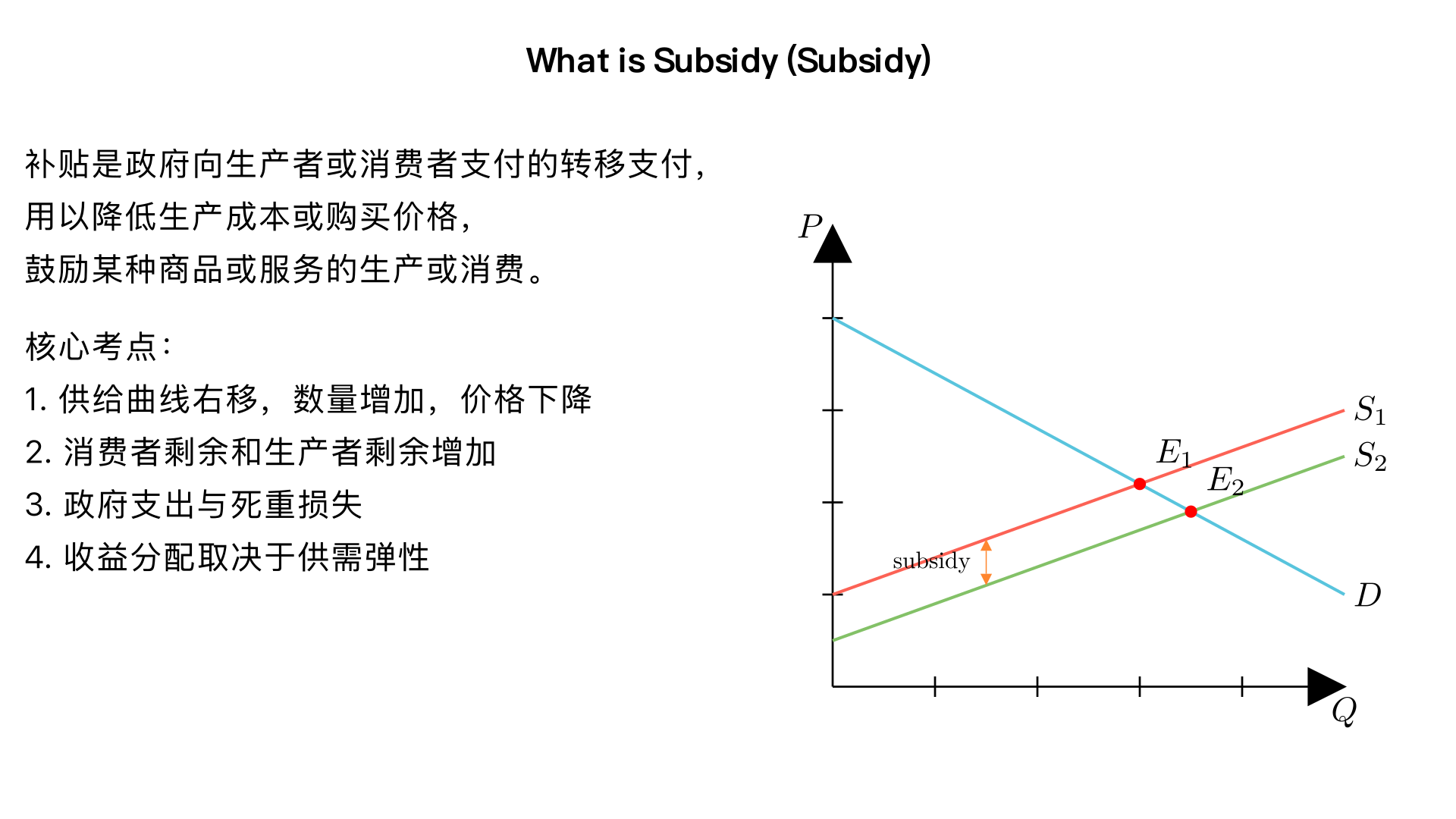
下面按爱德思 IAL(Edexcel IAL)考试的要求,围绕题目 “什么是 subsidy(补贴)” 给出考点覆盖、每个考点的考场讲解、常见题型、推荐答题结构与具体采分点(如何拿分)。语言以中文为主,便于考试时直接套用。 一、概念与标准定义(考点 + 如何拿分) - 定义(Key term,常为基础分) - 补贴(subsidy):政府向生产者或消费者支付的转移支付,用以降低生产成本或购买价格,鼓励某种商品或服务的生产/消费。 - 考场拿分点:写出“政府支付/降低成本/鼓励生产或消费”即能拿到定义分(K 分,通常1–2 分)。 二、核心分析考点(每点都常会在解释/分析题中被考到) 1. 类型与对象 - 按对象:生产者补贴(per-unit subsidy、lump-sum subsidy)或消费者补贴(voucher、tax credit)。 - 按目的:支持新产业、保障农产品、纠正外部性等。 - 考场要点:说明是哪种补贴并与题干案例对应(应用分,AP)。 2. 对供需的直接影响(必考) -生产者补贴:等同于单位成本下降 →供给曲线向右/下平移(每单位垂直距离等于补贴金额)。 - 消费者补贴:有效提高消费需求或相当于对需求的价格补贴。 - 考场要点:配合图示说明供给/需求如何移动(分析分,AN;图示通常为2 分)。 3. 对均衡价格与数量的影响 - 数量增加;市场价格下降(消费者支付更低价格),生产者得到的价格(含补贴)可能高于原价或变化取决于供需弹性。 - 考场要点:写清新旧均衡、谁最终受益(消费者/生产者)并解释机制(AN + AP)。 4. 分配结果:消费者剩余、生产者剩余、政府开支与死重损失(Welfare) -解释各自怎样变化并标明在图中的面积(CS ↑、PS ↑、政府支出=补贴×新产量、可能出现 DWL)。 - 考场要点:在图里标注并用文字说明面积变化,能得分(分析分)。 5.负担归属(税/补贴归宿)与弹性 - 补贴收益由谁获得取决于供需价格弹性:供给弹性大 → 劳多给消费者;需求弹性大 → 更多给生产者。 - 考场要点:用弹性讨论收益分配(评价/高阶分析点)。 6. 政策目标与替代方案 -目标:提高产量、支持产业、纠正正外部性、降低价格等;替代:税收优惠、公共供给、规制、直接补助低收入群体。 - 考场要点:分析补贴是否最优(EVA)。 7. 潜在问题与评价方向(常为评分中 EVA) -预算约束/机会成本(资金可用于教育/卫生等);死重损失与效率损失;道德风险、依赖、产能过剩、资源配置扭曲、国际贸易扭曲/补贴战;难以精确定位受益者(targeting 问题)。 - 考场要点:提出一到两个具体评价点并说明其影响与重要性(EVA 分)。 三、图示要求(考试中非常关键) - 要画的图:典型为供给-需求图(若分析外部性,可用边际社会成本/边际私人成本) - 必要标注:横轴数量 Q,纵轴价格 P;初始供给 S1,补贴后 S2(右移);初始均衡 E1 (P1,Q1),新均衡 E2 (Pc, Q2);标出生产者实际收到价格(Pc + subsidy)或用垂直距离标明补贴金额;标注 CS、PS、政府支出、DWL 区域。 - 拿分提示:清晰图+正确标注通常给2 分;用图说明 CS/PS/政府支出变化再加分(约2 分)。 四、常见题型与建议答题结构、采分点(下面给出可直接套用的结构与对应采分点/时间参考) -2 分题(very short) - 要点:写出清晰定义或一条直接影响(K2 分或 AN2 分)。 - 举例:“补贴是政府向生产者支付的款项,用以降低生产成本并鼓励产量增长。” -4 分题 -结构建议:K1–2 + AN 或 AP 或 短图2(2+2)。 -采分点:定义 + 简单机制或图示变化(例如供给右移,价格下降,数量上升)。 -6 分题 -结构建议:K2 + AN2 + AP2(举例或与素材联系)。 -采分点:定义;画/描述供给移动与均衡变化;用案例/数字或具体市场说明影响。 -8 分题(常见) - 推荐结构(与考试常用评分模板对应):K2 分,AN2 分,AP2 分,EVA2 分。 -详细说明: - K(2 分):给出补贴定义并说明对象(生产者/消费者)。 - AN(2 分):画图或描述供给/需求如何变化以及对 P、Q 的影响(数量上升、市场价下降)。 - AP(2 分):引用题干信息/案例(如补贴金额多大、目标行业、时间长短)并将其代入分析(如补贴大→政府支出大→DW L大)。 - EVA(2 分):短评(如预算约束、弹性影响、是否更好用税收或直接转移支付来替代)。 - 时间建议:8 分题约8–9 分钟答题(含1–2 分钟审题)。 -10/12/20 分题(长答题) -结构建议: - 简短引言:定义 + 政策目的(1–2句)。 - 主体分析:多面分析(图示,多点效果,分别讨论生产者/消费者/政府/社会福利,举例并结合题干)(主体占大部分分)。 -评价:讨论限制、弹性、目标替代方案、财政可持续性、长期影响等(多角度且深)。 -结论:根据论证给一个权衡性结论(哪种情况下支持或反对)。 -采分点:准确定义、完整图与面积变化、结合案例数据(AP)、多角度评价并给结论(EVA 很关键,尤其是12/20 分题)。 五、答题写作/考试技巧(快速拿分指南) - 开头先写清定义(确保拿到 K 分);若题目要求“with reference to Extract”,务必引用 extract 的关键信息(时间、数额、对象、目标)。 -画图并标注——图要清晰、标注完整(这是常见的2 分“必拿”)。写旁注解释图中各面积的含义。 -论证要分层次:先说明直接效果,再讲第二轮(例如长期成本下降/行业结构变化)。 -评价要具体:给出1–2 个与案例相关的限制/反对论据,并说明其对结果的影响(例如“若需求弹性很小,补贴主要流向生产者”)。 - 用实例或数字(若题干给出)来支持结论,能拿 AP 分。 - 时间管理:短题务必简洁;长题留2–3 分钟检查。回答要有结论/判断(尤其在高分题里)。 六、示例(8 分题答题提纲,便于直接套用) 1. 定义(约一句):补贴是政府向生产者/消费者支付的款项以降低成本/价格并鼓励生产或消费(K)。2. 图与分析(画图并解释,AN):画供给-需求图,供给右移,数量从 Q1 增至 Q2,市场价格从 P1 降到 Pc,生产者实际收到的价格为 Pc + s。说明 CS、PS、政府支出变化及可能的 DWL。3. 应用(AP):结合题干(例如“若补贴每单位100 元且期限2 年”)说明政府支出为100×Q2、短期内生产者获利/长期可能依赖等。4.评价(EVA):讨论预算约束、弹性影响(谁得益更多)、替代政策(如直接现金补贴或税收优惠)以及补贴可能造成的扭曲。并给出短结论:在 X 条件下补贴较合适/否则效果有限。 七、常见考官期望(拿分要点回顾) - 明确、准确的定义(K); - 用图或文字清楚描述机制(AN); - 与题干或实际数字结合(AP); - 有针对性的评价(EVA),并给出判断/结论(尤其高分题很重要)。 如果你愿意,我可以: - 给出一张示范图(描述版)并标注每一部分应写的文字说明;或- 按照你提供的一段 Extract(题干材料),把上面的8 分示例扩展为一篇可交卷的短答案(含具体引用与评价)。 需要哪一种请告诉我。
▶
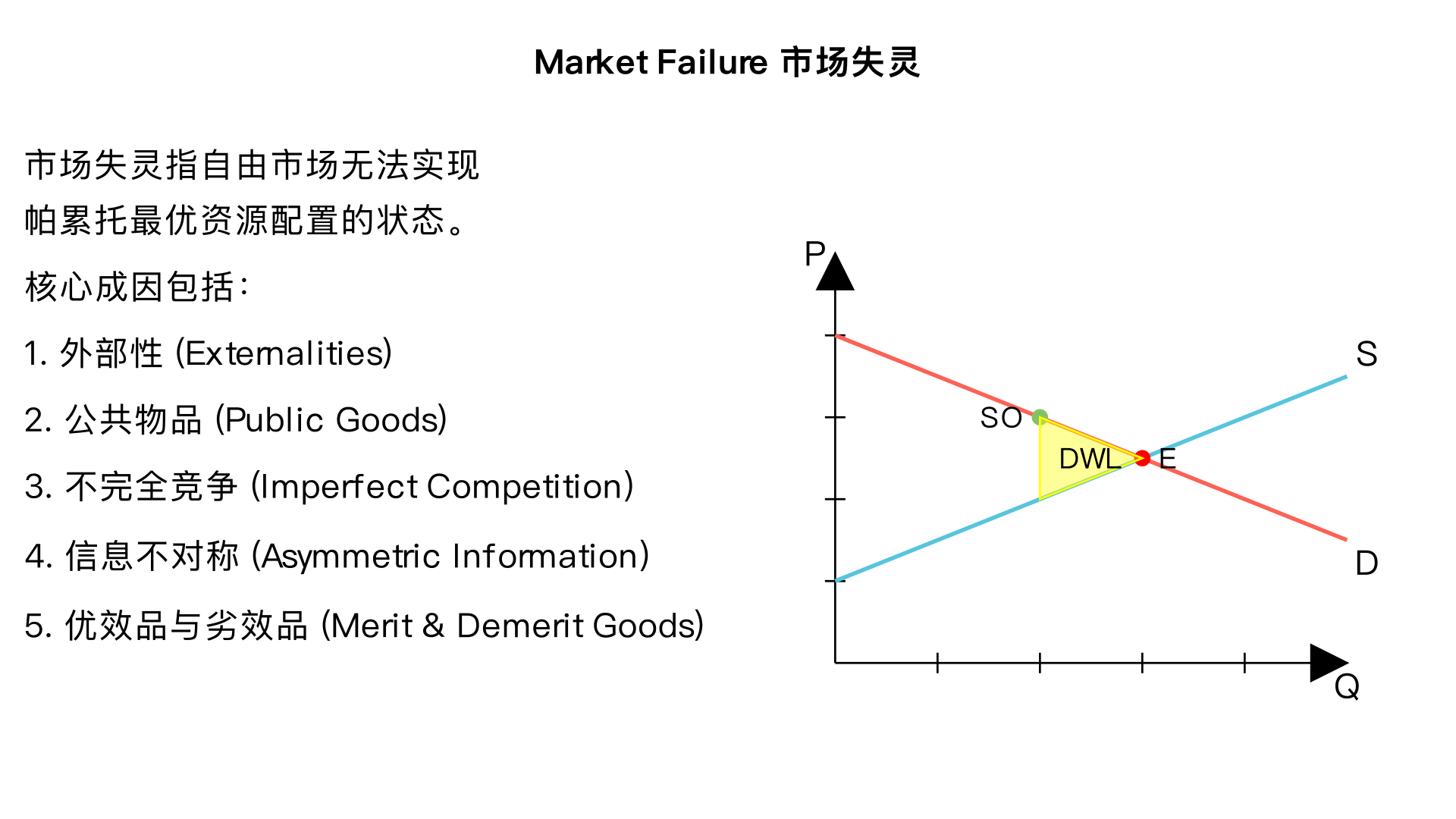
爱德思经济学框架下的 Market Failure 定义 Market failure 指的是自由市场在没有政府干预的情况下,无法实现资源的帕累托最优配置(Pareto efficient allocation of resources) 的状态。 这里的帕累托最优是指:在不损害其他人福利的前提下,无法再通过资源重新分配来提升任何人的福利水平。简单来说,自由市场的自发调节机制失效,导致资源分配出现扭曲,产生社会福利损失(deadweight loss)。 爱德思考点中 Market Failure 的核心成因 外部性(Externalities) 指经济主体的行为对第三方产生了未被市场价格反映的影响,分为两类: 正外部性(Positive externalities):第三方获益但无需付费,比如疫苗接种、基础教育,自由市场的供给量会低于社会最优水平。 负外部性(Negative externalities):第三方受损但未得到补偿,比如工厂污染、汽车尾气,自由市场的供给量会高于社会最优水平。 公共物品(Public Goods) 具有两个关键特征:非排他性(无法阻止他人免费使用)和非竞争性(一个人使用不影响其他人使用),例如国防、路灯。 由于 “搭便车问题”(free-rider problem),私人企业没有动力提供这类物品,自由市场会出现供给为零或严重不足的情况。 不完全竞争(Imperfect Competition) 当市场被垄断(Monopoly)、寡头垄断(Oligopoly)等势力控制时,企业会通过限制产量、抬高价格来获取超额利润,导致资源配置效率低于完全竞争市场,产生福利损失。 信息不对称(Asymmetric Information) 交易双方掌握的信息数量或质量存在差异,会引发两种问题: 逆向选择(Adverse selection):交易前信息不均,比如二手车市场中卖家隐瞒车辆缺陷,导致劣质商品驱逐优质商品。 道德风险(Moral hazard):交易后信息不均,比如购买保险后降低风险防范意识,增加保险公司的赔付成本。 优效品与劣效品(Merit & Demerit Goods) 优效品(Merit goods):社会认为对消费者有益,但消费者往往低估其价值,比如医疗、消防安全设备,自由市场供给不足。 劣效品(Demerit goods):社会认为对消费者有害,但消费者往往高估其价值,比如香烟、酒精,自由市场供给过剩。
▶
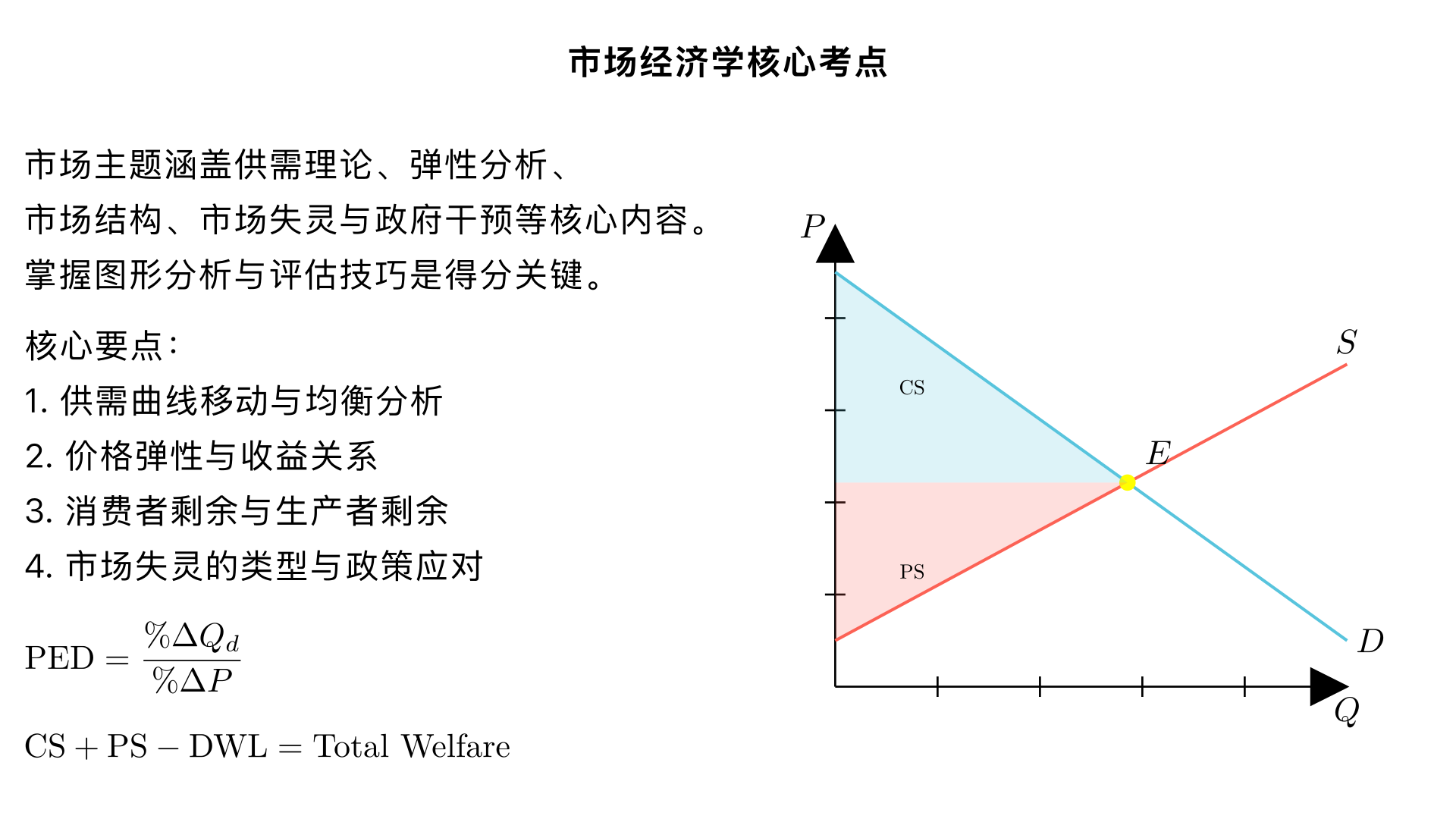
下面我按爱德思(Edexcel IAL)考试的要求,把“Market”这一主题覆盖的考点逐项列出、按考试要求给出每个考点的要点与答题要素,接着说明常见的题型、各题型的答题结构模板与采分点,最后给出常见失分点与考试技巧。语言和要点均以能在试卷上得分为目标设计。 一、“Market”主题覆盖的主要考点(每项后给出考场要点) 1.需求与供给(Demand & Supply) 要点:需求定律、供给定律及影响因素(价格以外的决定因素:收入、偏好、替代品/互补品、成本、技术等)。 必得内容:给出定义,画出供给/需求图(标清横轴:数量,纵轴:价格;标清原始均衡P0、Q0)。 考场写法:描述变动的原因→画图并指出曲线如何移动→说明新均衡P1、Q1方向与原因(数量或价格上涨/下降)。 常见采分点:正确定義(K)、正确画图并标注(图分)、明确曲线移动方向与对价量的影响(AN/AP)。 弹性(Price Elasticity of Demand/Supply, Income & Cross Elasticity) 要点:公式、解释(弹性>1弹性、<1inelastic)、影响总收益(TR)的变化规律。 必得内容:计算并解释;关联收入或替代品时解释实际含义。 考场写法:给出公式并计算(K/AP)、解释数值含义(AN)、结合图/实例说明对价格/税收政策的影响(EVA)。 -采分点:正确公式与单位、正确数值判断、对政策或收益的分析。 市场均衡与调整(Short-run & Long-run adjustment) 要点:外部冲击后的价格/产量如何调整,长期供给/需求弹性不同导致的结果。 必得内容:画短期/长期图,说明调整机制(如企业进入/退出、产能调整)。 -采分点:正确解释长期调整方向与机制(AN)。 市场结构(Perfect competition, Monopoly, Monopolistic competition, Oligopoly) 要点:特征比较(卖方数、产品同质性、进入退出壁垒、价格影响力);厂商行为(MR=MC 定价、平均成本、超额利润的存在/消失);长期均衡差别。 必得内容:对每种结构给出定义、画出适当的成本和收益曲线(如果要求利润影响要画MR、AR、MC、AC)、说明利润/产量/价格的影响。 -采分点:正确画图与标注(图分)、解释超额利润/正常利润的产生或消失(AN)。 消费者剩余与生产者剩余与福利分析- 要点:定义,怎样用供需图计算或显示价格变化造成的福利变化,死重损失(DWL)。 必得内容:在图上标注CS、PS、税收或垄断导致的DWL区域并解释。 -采分点:正确识别区域与解释福利变化来源(AP/AN)。 市场失灵(Market Failure) 要点:外部性(正外部性/负外部性)、公共物品(非排他性、非竞争性)、信息不对称、市场力量导致的效率损失、人口外部性与不完全竞争等。 必得内容:说明失灵类型的机制、用图示(例如负外部性:S私人与S社会的位移)并解释社会最优与市场均衡的差别。 -采分点:正确区分私人成本/社会成本或私人收益/社会收益并标出最优点与市场均衡(图分);解释福利影响(AN)。 政府干预与政策(税、补贴、价格上限/下限、规制、公共供给、课税与转移支付、产权界定) 要点:各政策的实施方式、在图上的表现(税楔、补贴楔、价格上限下限)、对价格、产量、税收负担、福利(CS/PS/DWL)的影响。 必得内容:画图显示税/补贴/限价的效果并分析税负分配(弹性决定谁承担较多)及DWL。 -采分点:正确图示与标注、把握弹性决定税负的原理、评估政策效果(短期/长期及边际成本/收益)。 8.交易成本、市场信息、博弈论(在寡头、合谋、价格战情景) 要点:信息不对称导致的逆向选择/道德风险、博弈的纳什均衡、寡头的策略(Kinked demand、价格领导、共谋)。 必得内容:描述问题生成机制并分析可能的结果或监管方法。 -采分点:概念准确、能应用到案例情形分析。 国际贸易与比较优势(如果“Market”涉及国际市场) 要点:比较优势基础、贸易造成的消费者/生产者影响、关税与配额的图解影响。 必得内容:解释贸易导致的福利变化、保护主义的影响与转移。 -采分点:正确图示并解释国内外价格与贸易量变化。 二、常见题型与答题结构(按爱德思IAL常见题型) 总体试卷构成(参照常见IAL/AS结构): -选择题(1分/题) 简答题(2、4分) 数据/案例问答(6、8、14分) Essay(20或30/40分) 下面给出每种分值题型的标准答题模板与考官采分重点: 1)1-2 分题(Definitions / very short answer) 答题要点:直接给出关键词定义或简单事实。 模板:精确定义(K),若需要可加一短句例子(+AP)。 -采分点:抓住关键词(比如“需求是……在一定价格下消费者愿意且能够购买的数量”)。 2)4 分题(简短分析) 常见题型:解释某一影响或画图。 推荐结构(来自上下文中的常用模板):K(1)+AP(1,引用题干)+AN(2,深入分析)。 如果要画图:图(1-2分)+写出图中的变动与原因(余分)。 -采分点:定义/图正确(图分),清楚地说明影响路径与方向(AN)。 3)6 分题(较完整的分析) 模板:K(1)+AP(2,引用题干细节)+AN(3,逐步分析导致的变化)或 图 +解释 +影响。 -采分点:逻辑清晰、图示与文字互相支持、能指出短期与长期不同结果(若相关)。 4)8 分题(结构化要求高) 推荐结构(按给的模板非常适用):K2分、AN2分、AP2分、EVA2分。 K:给出关键概念或定义(2分)。 AN:对变化或机制做深入分析(2分)。 AP:引用并结合题干事实(2分,例如数值、情境说明)—注意写明如何在该情境下发生。 EVA:评估/限定条件(2分),给出替代结果、影响的大小/持续性或政策建议。 图形提示:若题目要求画图,画图并在论述中解释图中变化并标注超额利润/税收等(图分通常在2分左右)。 -采分点:每一部分都要有对应内容才能拿满分;评估部分非常关键(例如讨论规模、时间、弹性、替代影响等)。 5)14 分题(较长的分析+评估) 建议结构(分段清晰): 开头(2-3分):定义与定位(K)。 主体分析(6-7分):逐步分析机制并结合图形(若相关),对不同情境(短期/长期)分别讨论。 -评估(4-5分):权衡利弊,讨论假设、条件、相反论证、政策替代方案、结论的限制并给出结论性判断。 -采分点:深度分析+有效评估是关键;使用数据或实例可以加分。 6)20/30/40 分Essay(大题) 建议结构: 引言:清晰定义与范围、文章路线图。 主体段(多个段落):系统展开论点,包括理论分析、图形、案例证据、反面论证与反驳。 -评估部分:讨论局限性、替代解释、政策权衡、分配效应、短长期差别等。 -结论:总结并做有依据的判断。 -采分点:逻辑结构、理论深度、评估质量、用例与图表的运用、最终判断的合理性。 三、常用图表清单(考试中必须会画并能解释) -需求/供给基本图与曲线移动- 弹性示意图(弹性与不弹性对TR的影响) 税收:税楔图并标出税收收入与DWL- 补贴:补贴楔并示意消费者/生产者受益与财政成本- 垄断:AR=需求,MR曲线,MC、AC 与利润矩形与DWL- 完全竞争长期/短期成本曲线(MC、AC、AVC) -负/正外部性:私人成本/社会成本或私人收益/社会收益曲线与社会最优-价格上限/下限引起的短缺/剩余与黑市分析- 寡头:kinked demand 或 payoff 矩阵(简要) 四、常见的采分细则与考场注意点(检查清单) 定义要准确、句子简练(拿K分)。 图像要:标明轴、标注曲线名称、标出原均衡与新均衡、标注关键面积(CS/PS/DWL/税收)。 分析要有因果链:原因 → 曲线移动/机制 → 对价格/产量/福利的影响(AN/AP)。 -评估要实质:不能只说“it depends”,要说明“取决于X(弹性/规模/持续时间/替代性),因此……”并给结论。 -结合题干信息(尤其Data/Extract题)引用数值或情境(AP)。 若涉及税和补贴,要讨论税负分配,并用弹性解释。 时间维度:短期与长期结果往往不同,考试常给分给说明两者差异者。 -语言:用经济术语(elastic/inelastic, deadweight loss, social cost, consumer surplus等),不要泛泛而谈。 五、常见扣分点与避免方法- 图不完整或未标注名称/均衡点 → 丢图分。 -只画图不解释,或只文字不画图(若题目要求图,两者都要)。 -评估过浅(如仅一句“depends”) → 丢评估分。 概念模糊(混淆平均成本与边际成本) → 丢定义/分析分。 忽略题干情境(没引用Extract) → 丢AP分。 六、快速答题模板(面向常见题型) -2分:给出精确定义或直接答案。 -4分(影响类):定义/说明(1)→ 引用题干/图(1)→解释原因与结果(2)。 -6分(图解或因果):画图(1-2)→解释曲线移动与新均衡(3)→ 小结影响(1)。 -8分:K2、AN2、AP2、EVA2(按此分配写作)。 -14分:定义+系统分析(短/长期、不同群体影响)+深入评估(讨论假设/弹性/替代/政策)+结论。 七、考前复习建议(针对Market主题) 熟练画并解释所有常用图(每种图都能画出并用文字解释2-3句)。 熟练掌握弹性计算及其政策含义(税收、补贴、价格控制影响)。 -练习8分和14分题,严格按模板计时练习,并在答案中加入限定条件和评估。 背诵几个现代真实世界的简短例子(如某国对电动车补贴、最低工资、碳税、垄断企业的案例)用于AP/举例。 如果你愿意,我可以: 给出一个标准化的8分范例答案(按K2 AN2 AP2 EVA2)针对一个具体题目(例如“分析政府对某商品的补贴会如何影响市场”)。 或者基于你提供的考题或Extract,帮你写一份分数对应的答题草稿。你想要哪一种?
▶
主题7、善易不卜 核心内容:探讨学习《易经》的终极目的,提出真正通晓易理的人,其境界超越单纯的吉凶占卜。 关键要点: 1. 哲学升华:引用孔子“不占而已矣”和荀子“善为易者不占”,强调《易经》的首要价值在于其哲学与伦理智慧。 2. 占卜本质:指出占卜(卜卦)的真正目的,是帮助决策者澄清思路、收集信息、引发潜能,而非迷信预言。 3. 核心能力:通过学习《易经》,培养洞察规律、审时度势的能力,从而主动“趋吉避凶”。
▶
7、善易不卜 核心内容:探讨学习《易经》的终极目的,提出真正通晓易理的人,其境界超越单纯的吉凶占卜。 关键要点: 1. 哲学升华:引用孔子“不占而已矣”和荀子“善为易者不占”,强调《易经》的首要价值在于其哲学与伦理智慧。 2. 占卜本质:指出占卜(卜卦)的真正目的,是帮助决策者澄清思路、收集信息、引发潜能,而非迷信预言。 3. 核心能力:通过学习《易经》,培养洞察规律、审时度势的能力,从而主动“趋吉避凶”。
▶
6、易有三义 核心内容:深入阐释《易经》书名中“易”字所包含的三层核心哲学含义,这是理解易学思想的关键。 关键要点: 1. 变易:宇宙一切现象永远处在变动不居之中,《易经》揭示的就是这种变化的规律。 2. 不易:在永恒的变化之中,存在着永恒不变的“道理”或“规律”,如阴阳消长的法则。 3. 简易:复杂的变化可归结为简单的原理(如阴阳),智者能掌握原理,以简易的方法处理繁杂事务。
▶
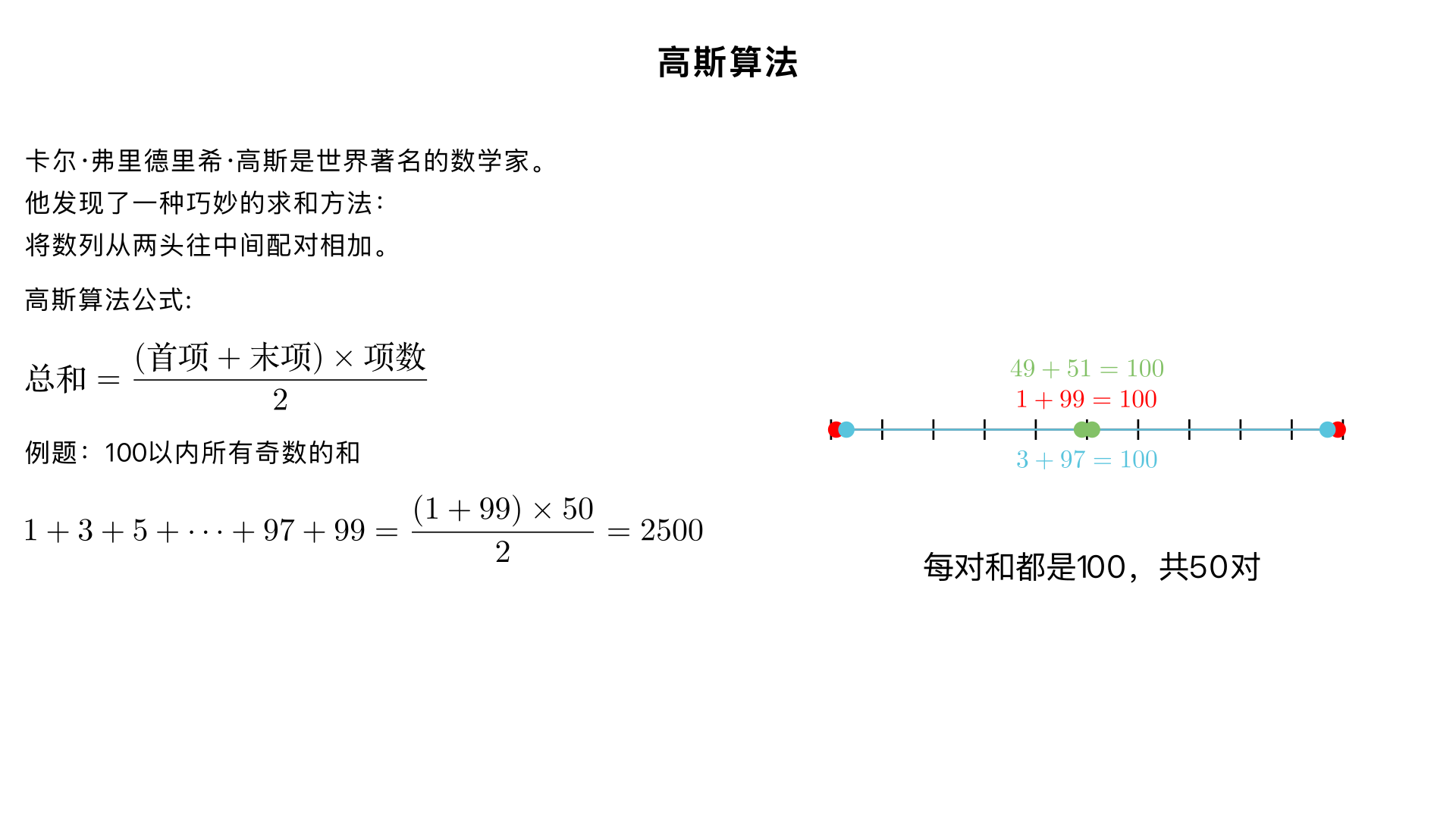
This image does not contain a geometric figure in the context of a mathematical problem or diagram. It contains text and a decorative, irregular outline. Therefore, I will proceed with extracting the content. **Extracted Content:** **Title:** 高斯算法 (Gaussian Algorithm) **Main Explanatory Text:** 卡尔·弗里德里希·高斯 (1777—1855) 是世界著名的数学家。高斯出生在德国的一个贫困家庭,由于家境贫寒,他没有受过什么早期教育,但他很小的时候聪颖过人,特别爱动脑筋,有很高的数学天赋。 老师出完题目没过一会儿,小高斯就脱口说出了正确答案:5050。并说出自己的巧妙算法。原来他通过细心的观察,发现1—100这一列数从两头往中间逐“对”相加,每一“对”的和都是101。一共有50(100÷2)个数对,它们的总和当然是5050。 注:在数学上,人们把每相邻两个数的差都相等的一串数称作等差数列。归纳出一个通用的算术数列的求和公式,就是: 这 就是大名鼎鼎的“高斯算法”公式,你一定要记住啊。 **Mathematical Formula:** 高斯算法: 总和 = (首项+末项)×项数÷2 **Section Title:** 1. 简单数列 (Simple Sequence) **Example Problem (例题):** 100以内所有奇数的和是多少? (What is the sum of all odd numbers within 100?) **Solution/Analysis (解析):** 100以内所有的奇数是:1, 3, 5, 7, …, 97, 99. 一共有50个数(也叫作50个“项”), 每相邻两个数之间的“差”都是2, 叫作“公差”。知道了这些就可计算它们的总和了: 1+3+5+…+97+99 =(1+99)×50÷2 =2500. **Answer (答):** 100以内所有奇数的和为2500。 **Chart/Diagram Description:** * **Type:** Irregular decorative outline. * **Main Elements:** A hand-drawn, irregular, enclosed shape (resembling a cloud or speech bubble outline) is present on the right side of the page, framing the title "高斯算法". It serves a decorative purpose and does not represent a data chart or a geometric figure relevant to a mathematical problem.
▶
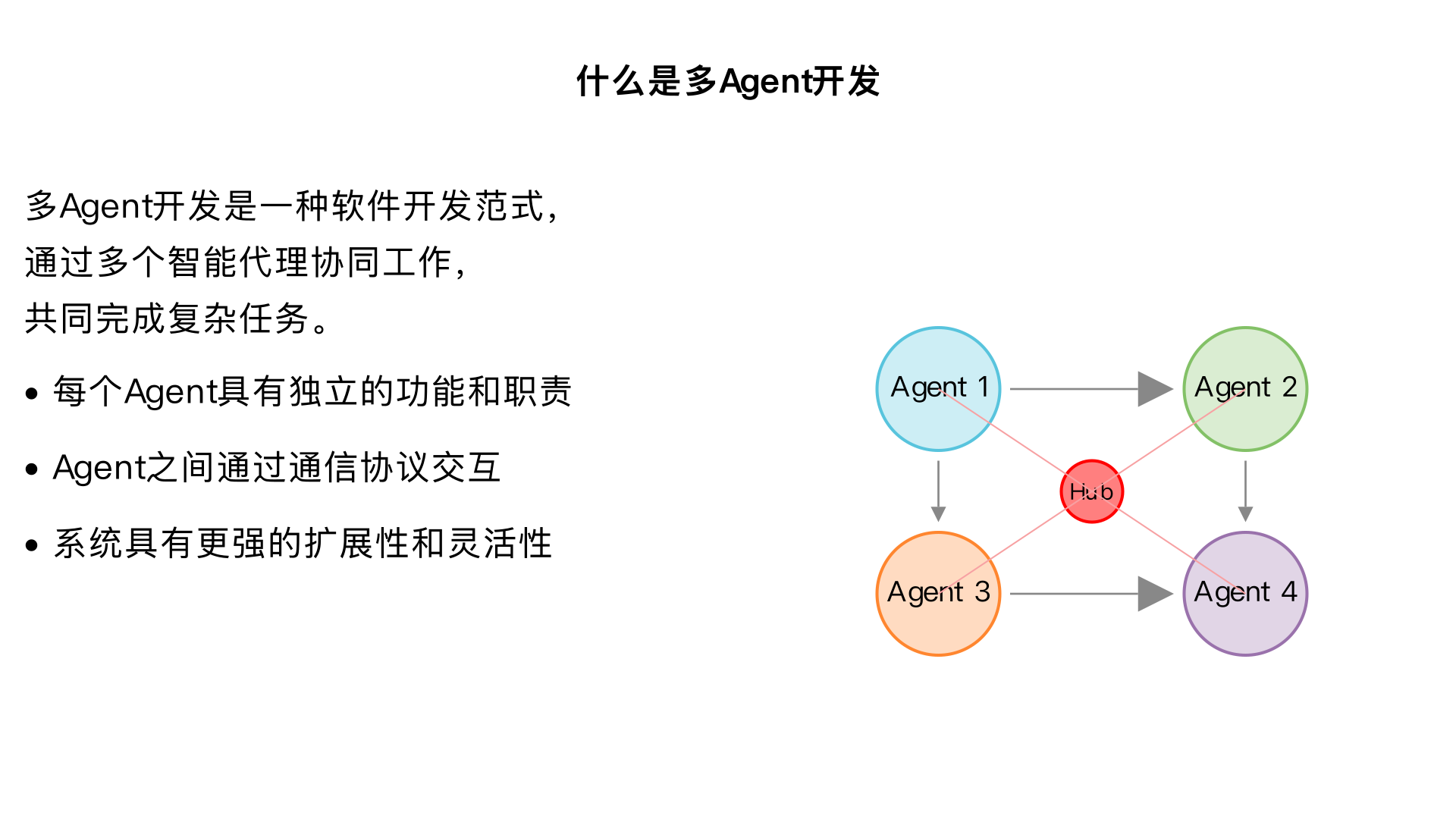
什么事 多Agent开发

▶
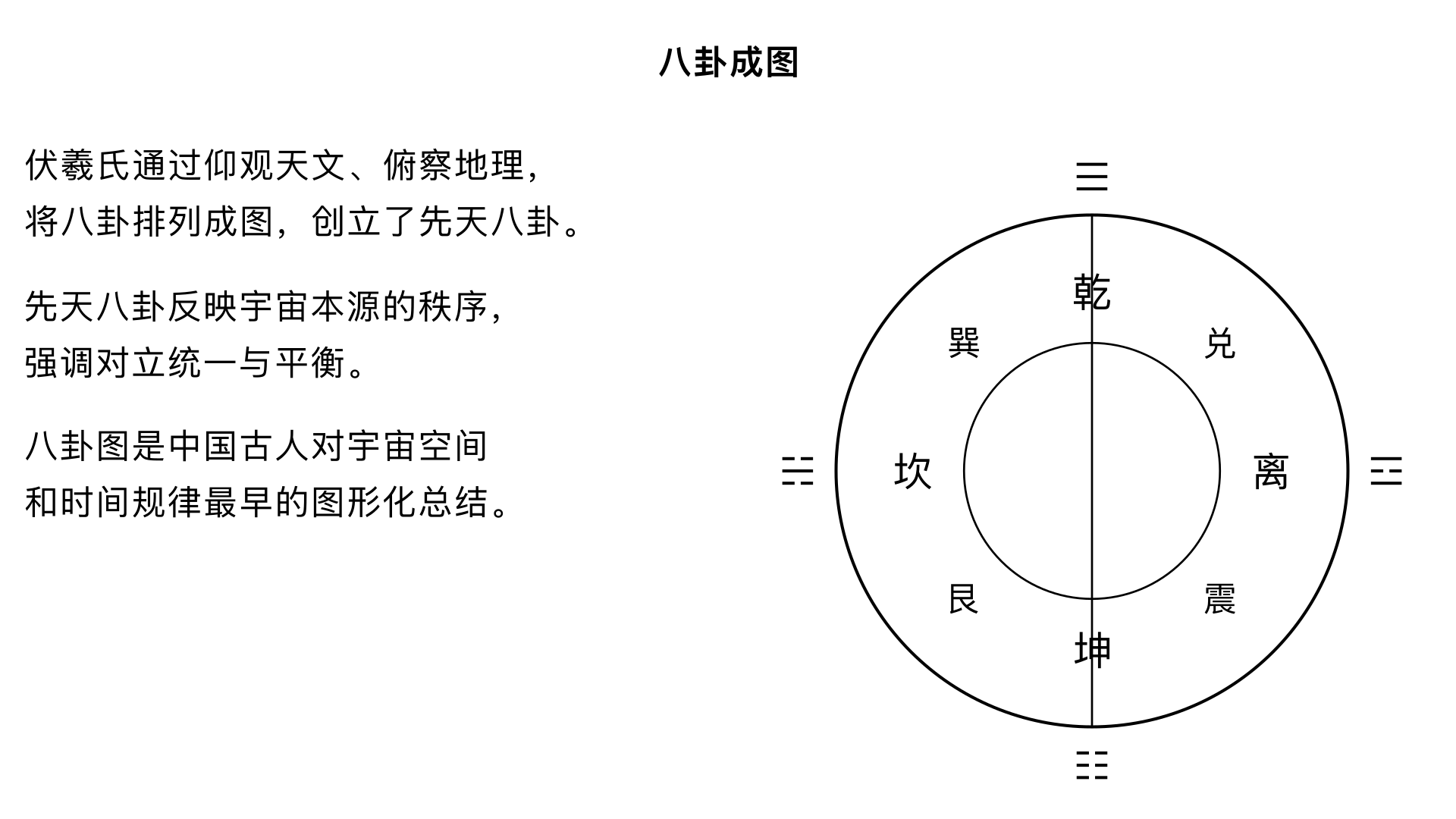
5、 八卦成图 核心内容:讲述伏羲氏在创立八卦后,如何通过“仰观天文,俯察地理”将其排列,从而绘制出伏羲先天八卦图的过程与深意。 关键要点: 1. 创立过程:伏羲通过长期观察与思索,根据自然地形与宇宙法则分配八卦方位。 2. 先天之理:先天八卦图反映了宇宙本源的秩序和状态,是“体”,强调对立统一与平衡。 3. 文化地位:八卦图是中国古人对宇宙空间和时间规律最早的图形化总结之一。
▶