T
Teach Me AnythingTMA
Video History
Page 4 / 47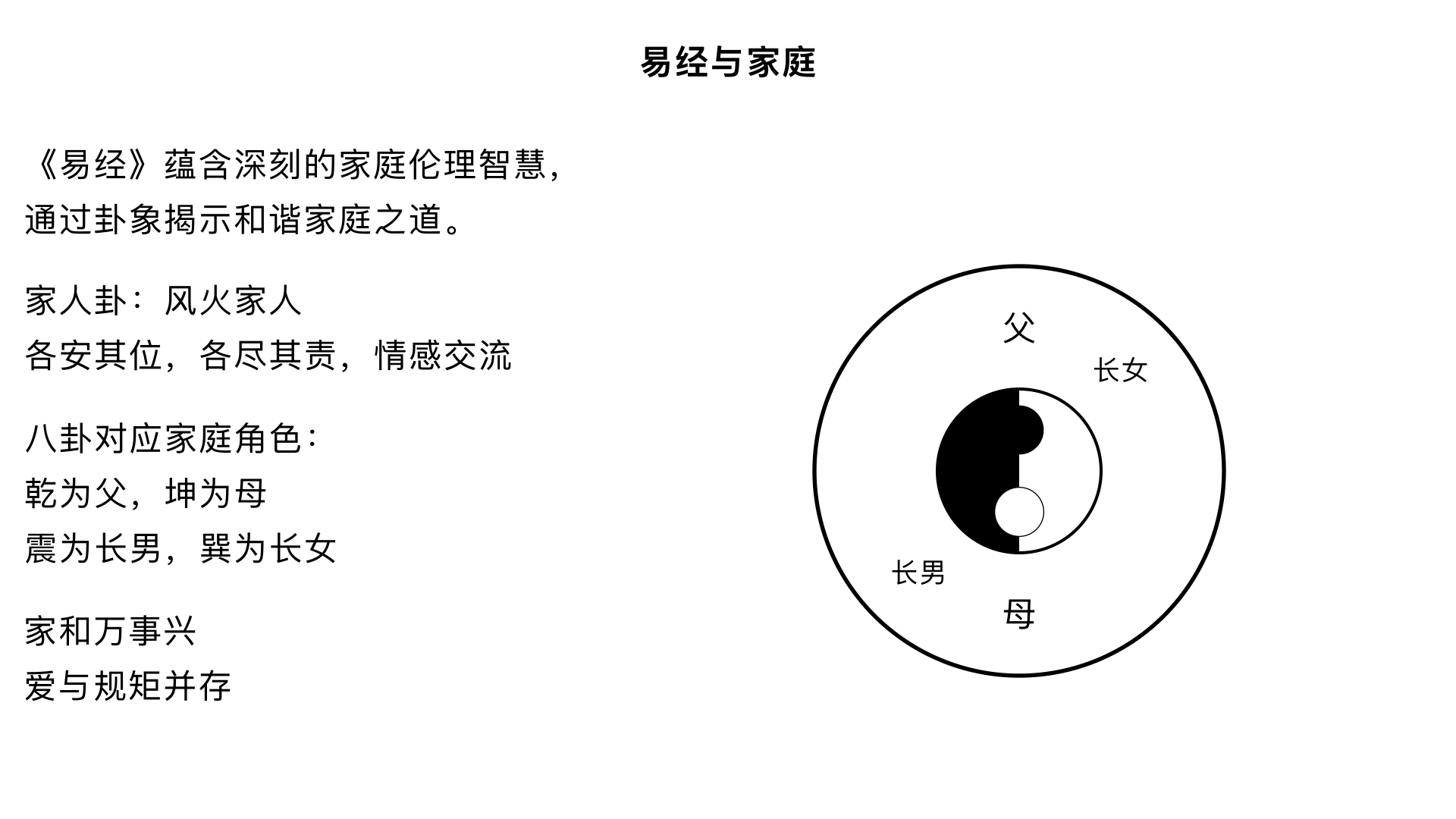
▶
13、易经与家庭 核心内容:将易理应用于现代家庭生活,阐释《易经》中的家庭伦理观(如家人卦),探讨如何构建和谐稳固的家庭关系。1313、 关键要点: 1. 家庭卦象:重点解析“风火家人”卦,强调各安其位、各尽其责、情感交流的家庭伦理。 2. 角色对应:八卦可类比家庭角色:乾为父、坤为母,震为长男等,阐明不同角色的责任与相处之道。 3. 和谐之道:家庭和谐的基础是爱与规矩并存,最终实现“家和万事兴”。
▶
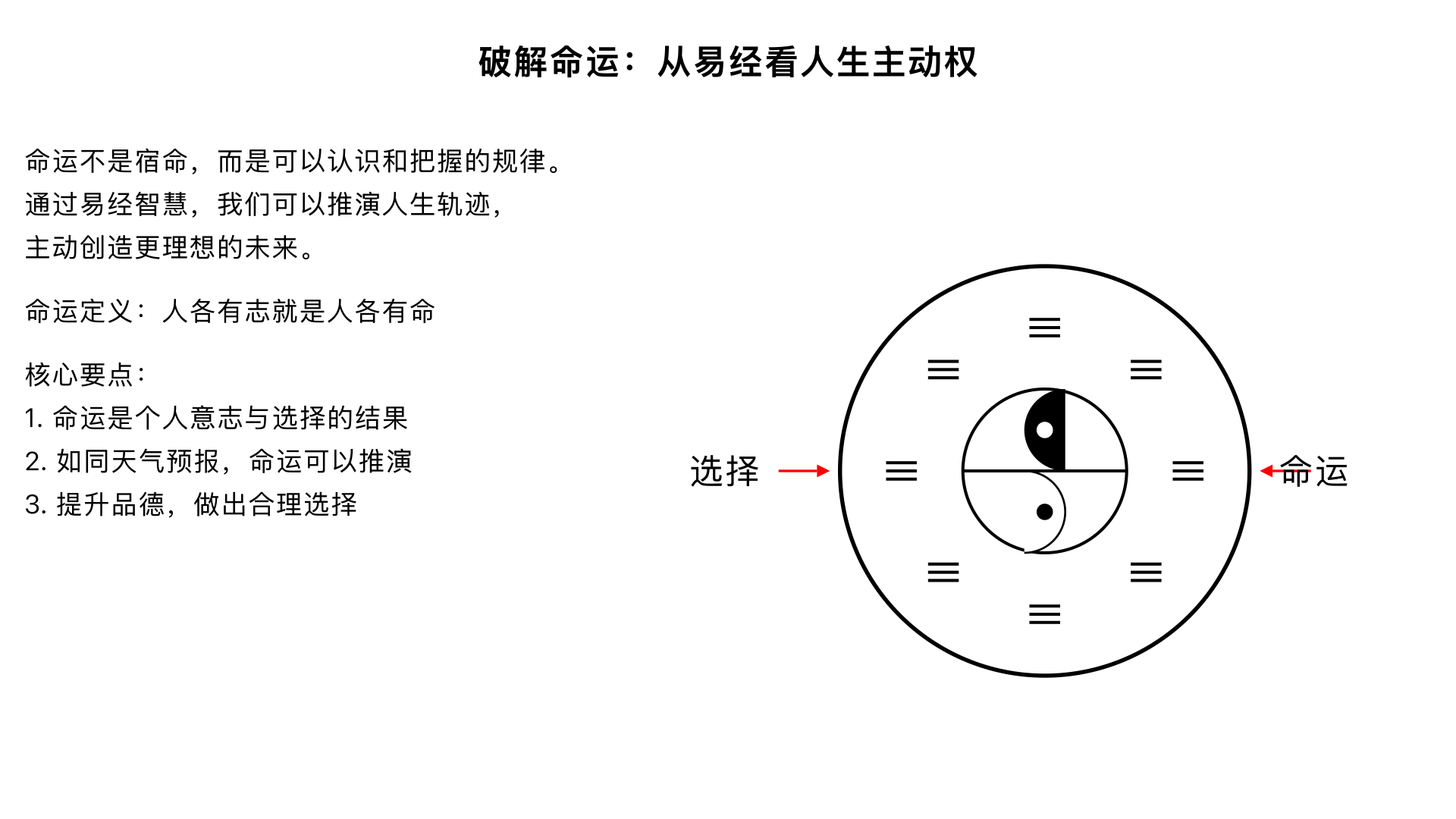
主题12、破解命运 核心内容:从《易经》角度探讨“命运”的本质,论证命运是一种可以认识和把握的“自然规律”,从而将人生的主动权交还给自己。 关键要点: 1. 命运定义:“人各有志就是人各有命”,命运是个人意志与选择长期作用下的结果,是一种潜在的规律。 2. 可知可改:如同天气预报,命运(人生轨迹)也可以通过《易经》智慧进行推演和把握。 3. 主动创造:核心在于了解规律、提升品德、做出合理选择,从而创造更理想的命运。
▶
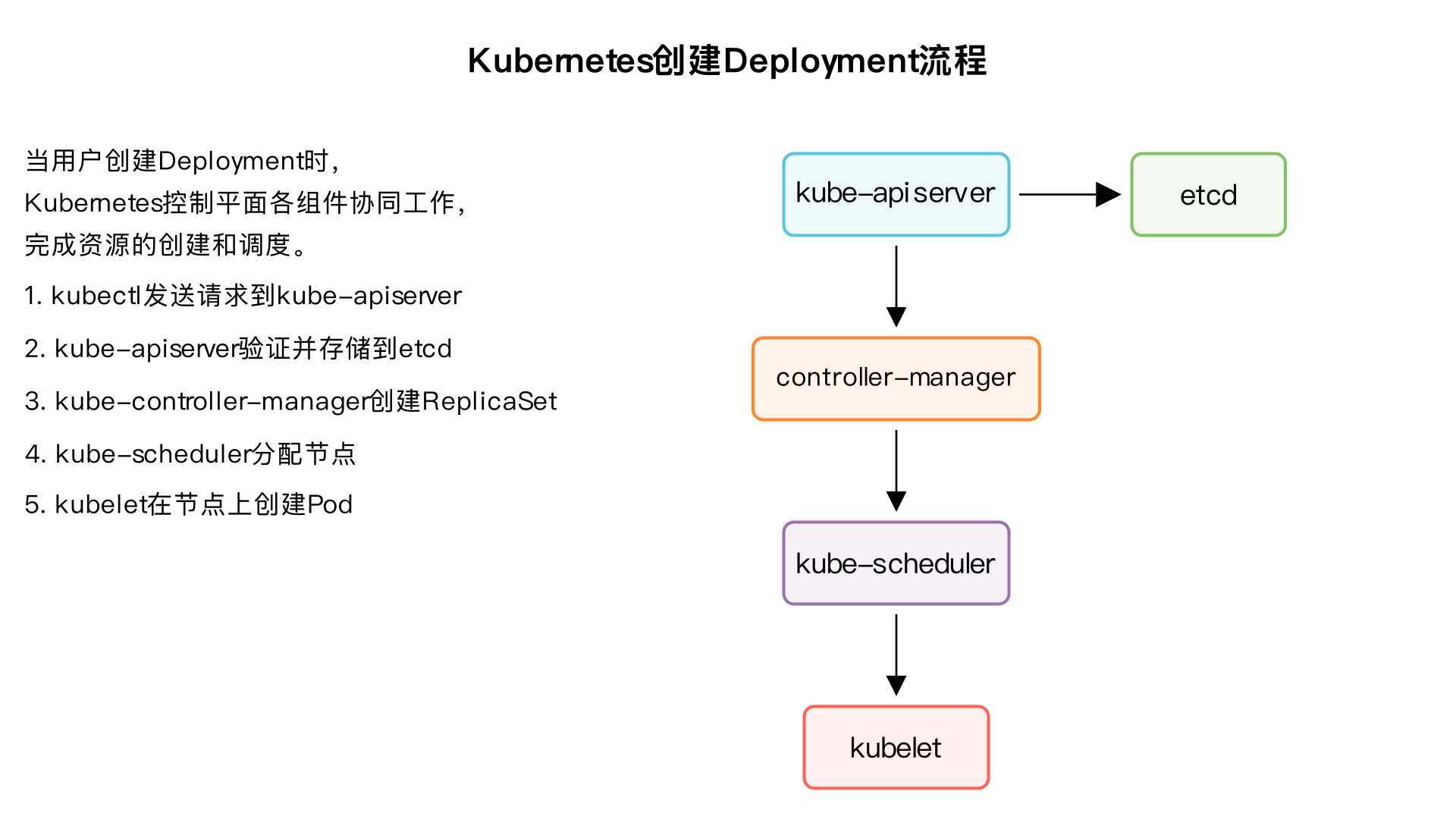
请帮我生成一段kubernetes创建deployment时,各控制平面组件的协作流程。要包含kube-apiserver,kube-suleduler,kube-controller-manager,kubelet,etcd,前后顺序一定要搞对
▶
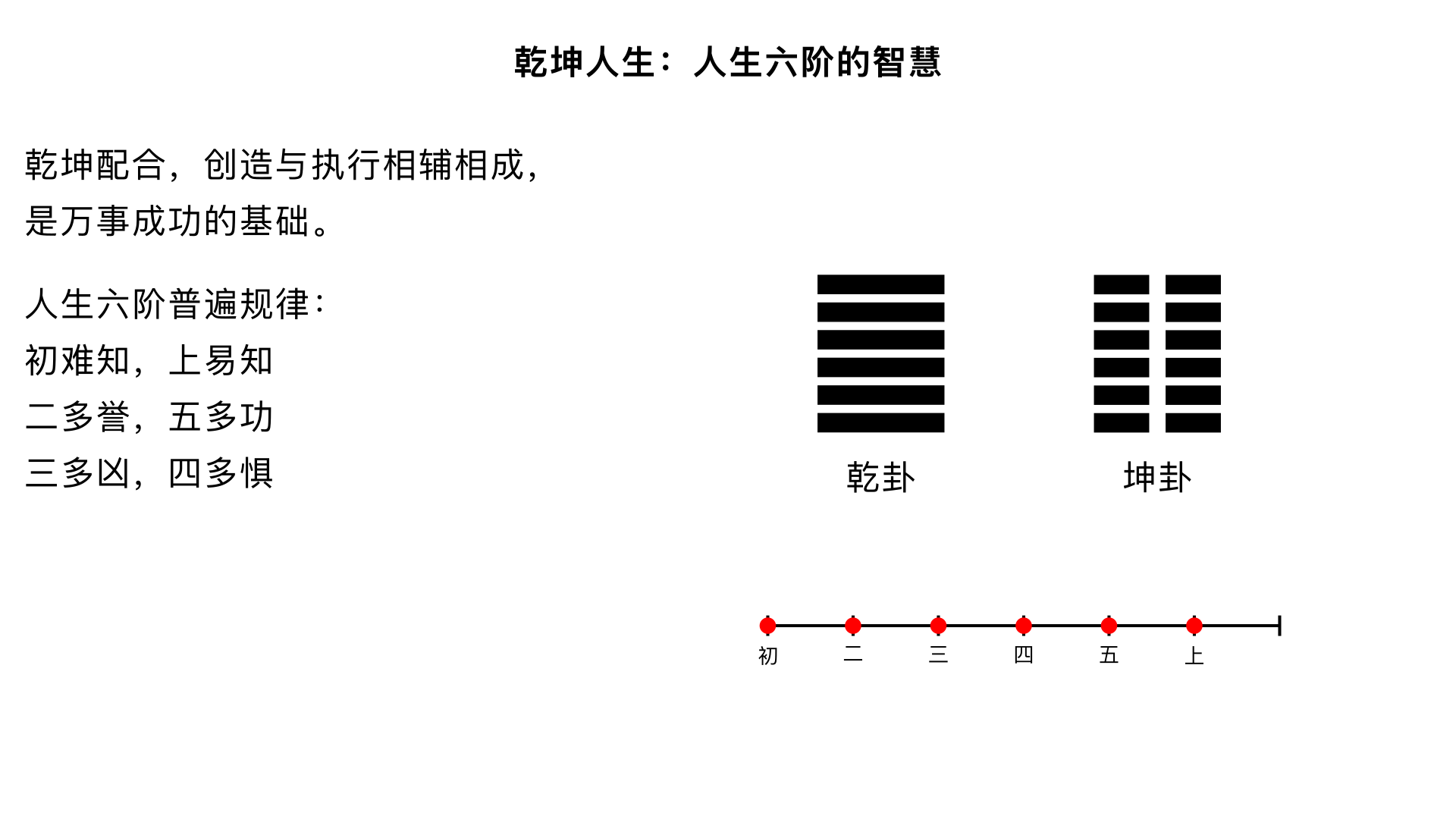
主题11、乾坤人生 核心内容:综合乾、坤两卦的智慧,将其对应到人生与社会角色中,分析人生不同阶段的普遍规律与应对策略。 关键要点: 1. 乾坤配合:乾(创造/领导)与坤(执行/配合)相辅相成,是万事成功的基础。 2. 人生六阶普遍规律: - 初难知,上易知:开始难预测,结局易看清。 - 二多誉,五多功:第二阶段多获赞誉,第五阶段多建功业。 - 三多凶,四多惧:第三阶段多险阻,第四阶段多戒惧。
▶
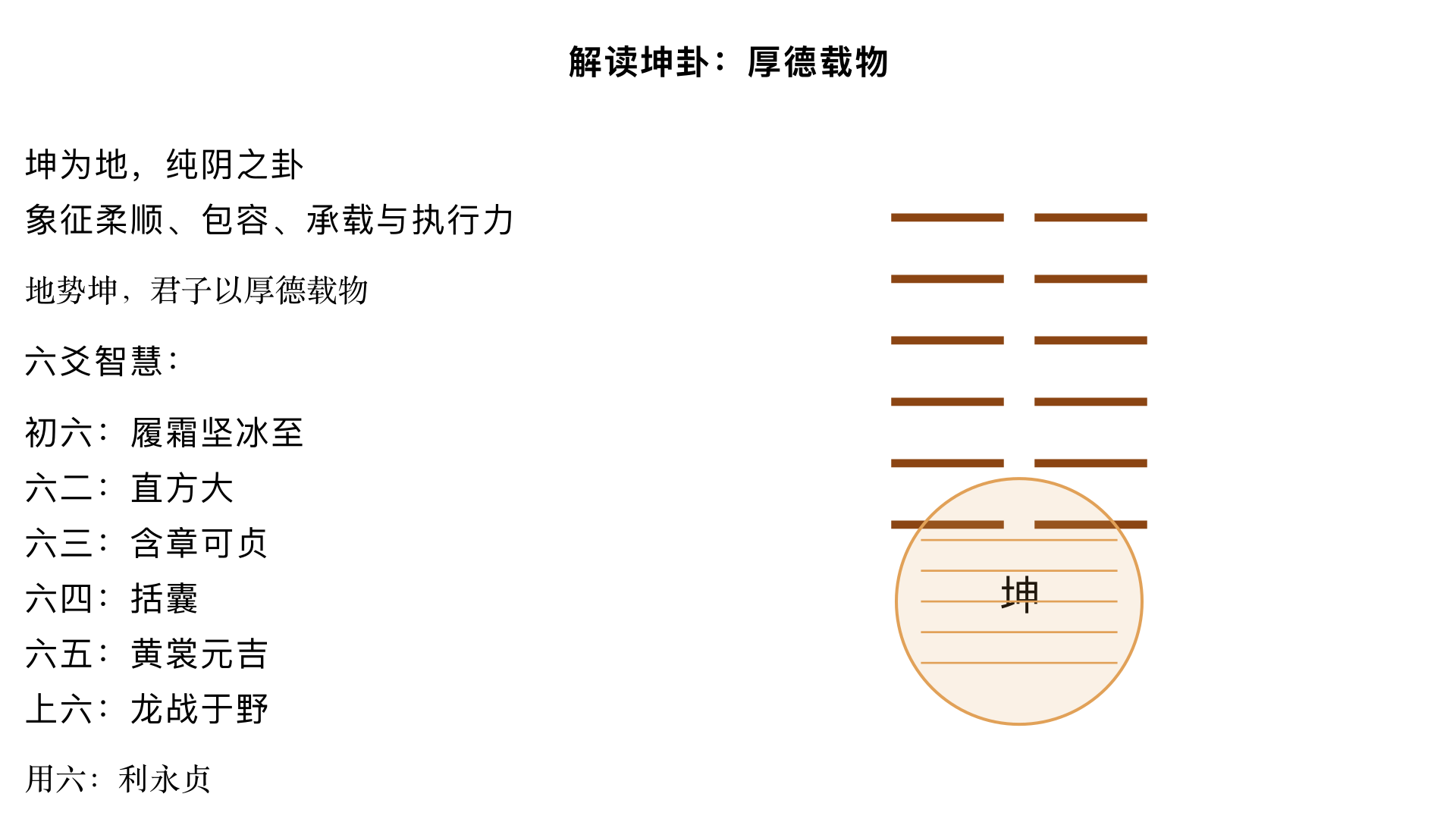
主题10、解读坤卦 核心内容:深度解读《易经》第二卦、纯阴之卦——“坤为地”卦,阐述其作为承载精神的代表,所蕴含的柔顺、包容与辅佐之道。 关键要点: 1. 核心精神:“地势坤,君子以厚德载物”,象征柔顺、包容、承载与执行力。 2. 六爻智慧:详解其六爻: 初六(履霜坚冰至)- 六二(直方大)- 六三(含章可贞)- 六四(括囊)- 六五(黄裳元吉)- 上六(龙战于野)。 3. 用六真谛:“利永贞”,强调持守柔顺、安守本分才能获得长久吉祥。
▶
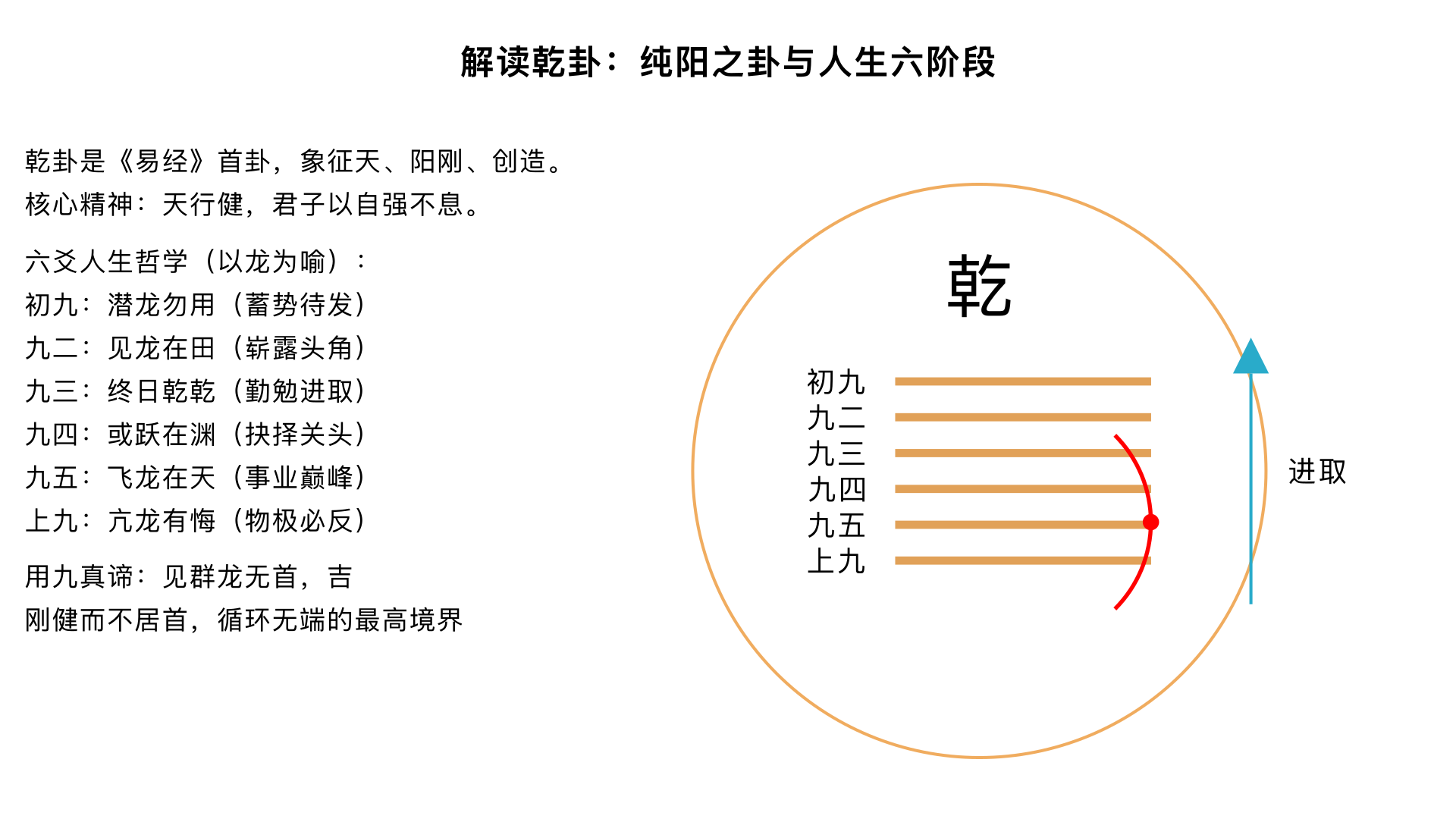
9、解读乾卦 核心内容:深度解读《易经》首卦、纯阳之卦——“乾为天”卦,剖析其作为开创精神的代表,所蕴含的人生六阶段发展哲学。 关键要点: 1. 核心精神:“天行健,君子以自强不息”,象征阳刚、创造、进取的力量。 2. 六爻人生:以“龙”为喻,详解六爻: 初九(潜龙勿用)- 九二(见龙在田)- 九三(终日乾乾)- 九四(或跃在渊)- 九五(飞龙在天)- 上九(亢龙有悔)。 3. 用九真谛:“见群龙无首,吉”,揭示刚健而不居首、各尽其责、循环无端的最高境界。
▶
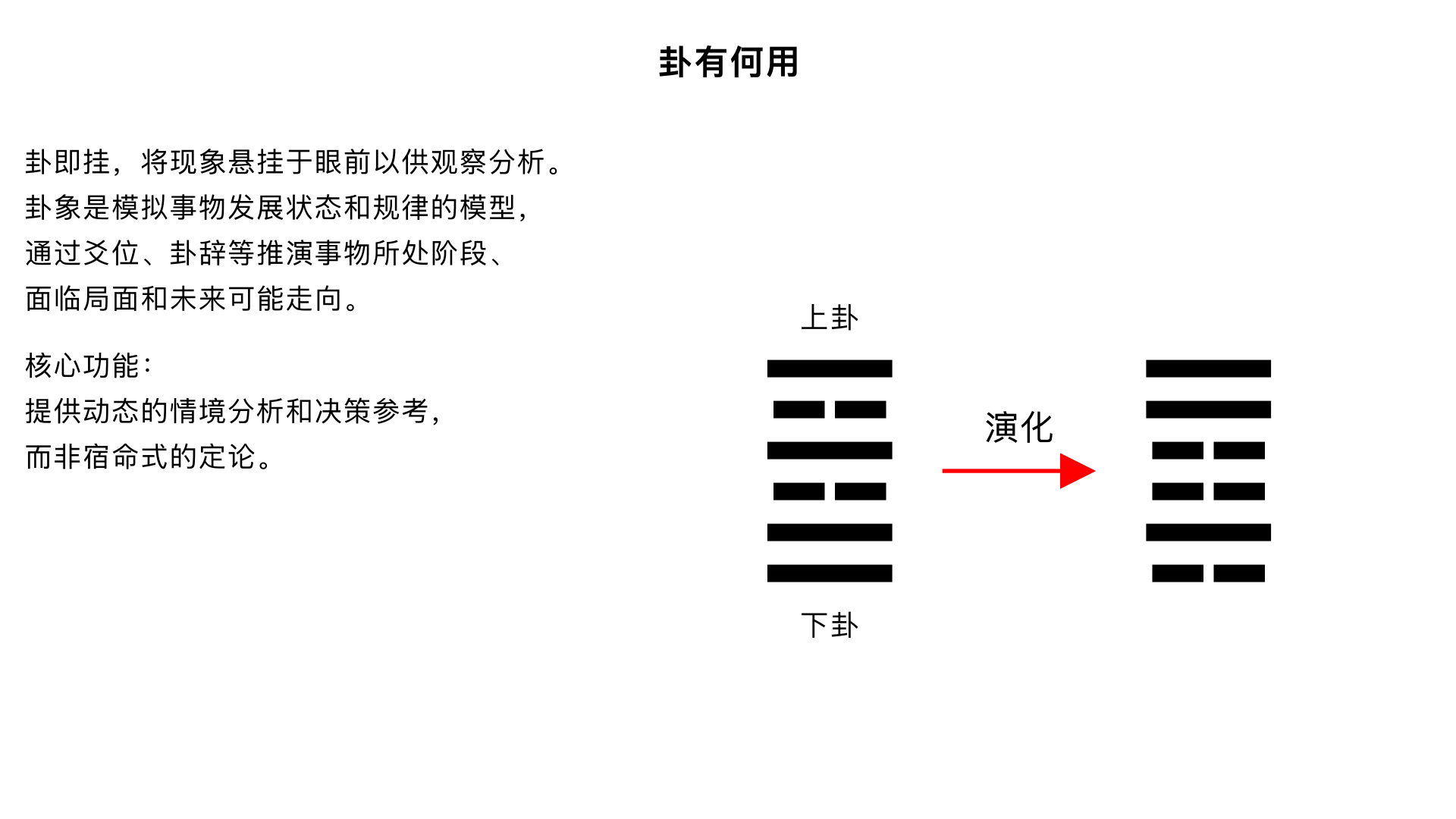
卦有何用 核心内容:讲解卦象(六十四卦)的实际功能和作用机制,说明如何通过解读卦象来理解事物的发展趋势与应对之道。 关键要点: 1. “卦”的本义:“卦”即“挂”,意为将现象悬挂于眼前以供观察分析。 2. 核心功能:卦象是模拟事物发展状态和规律的模型,通过其爻位、卦辞等,可以推演事物所处的阶段、面临的局面和未来的可能走向。 3. 决策参考:卦象提供的是一个动态的“情境分析”和“决策参考”,而非宿命式的定论。
▶
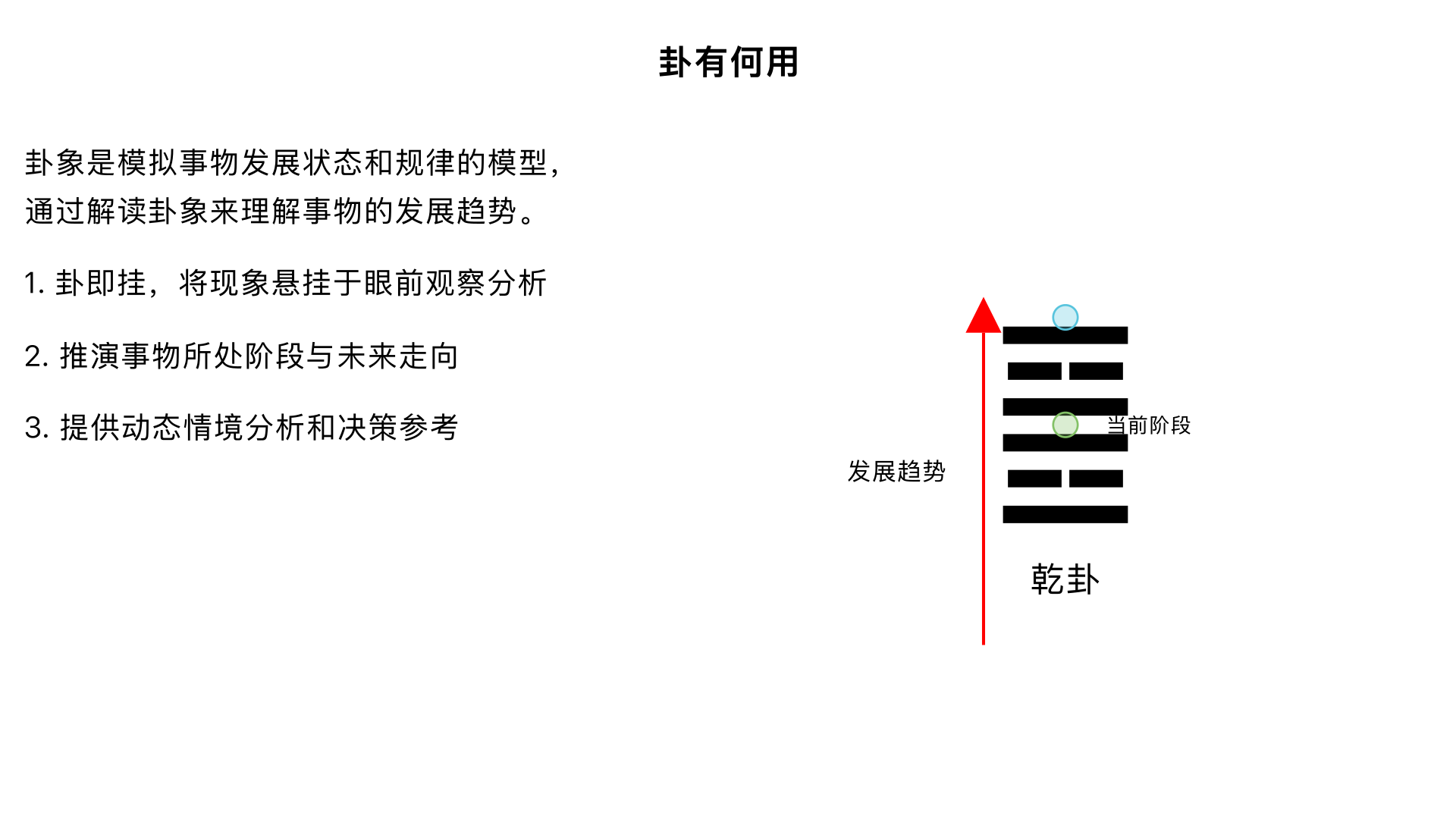
主题7、卦有何用 核心内容:讲解卦象(六十四卦)的实际功能和作用机制,说明如何通过解读卦象来理解事物的发展趋势与应对之道。 关键要点: 1. “卦”的本义:“卦”即“挂”,意为将现象悬挂于眼前以供观察分析。 2. 核心功能:卦象是模拟事物发展状态和规律的模型,通过其爻位、卦辞等,可以推演事物所处的阶段、面临的局面和未来的可能走向。 3. 决策参考:卦象提供的是一个动态的“情境分析”和“决策参考”,而非宿命式的定论。
▶
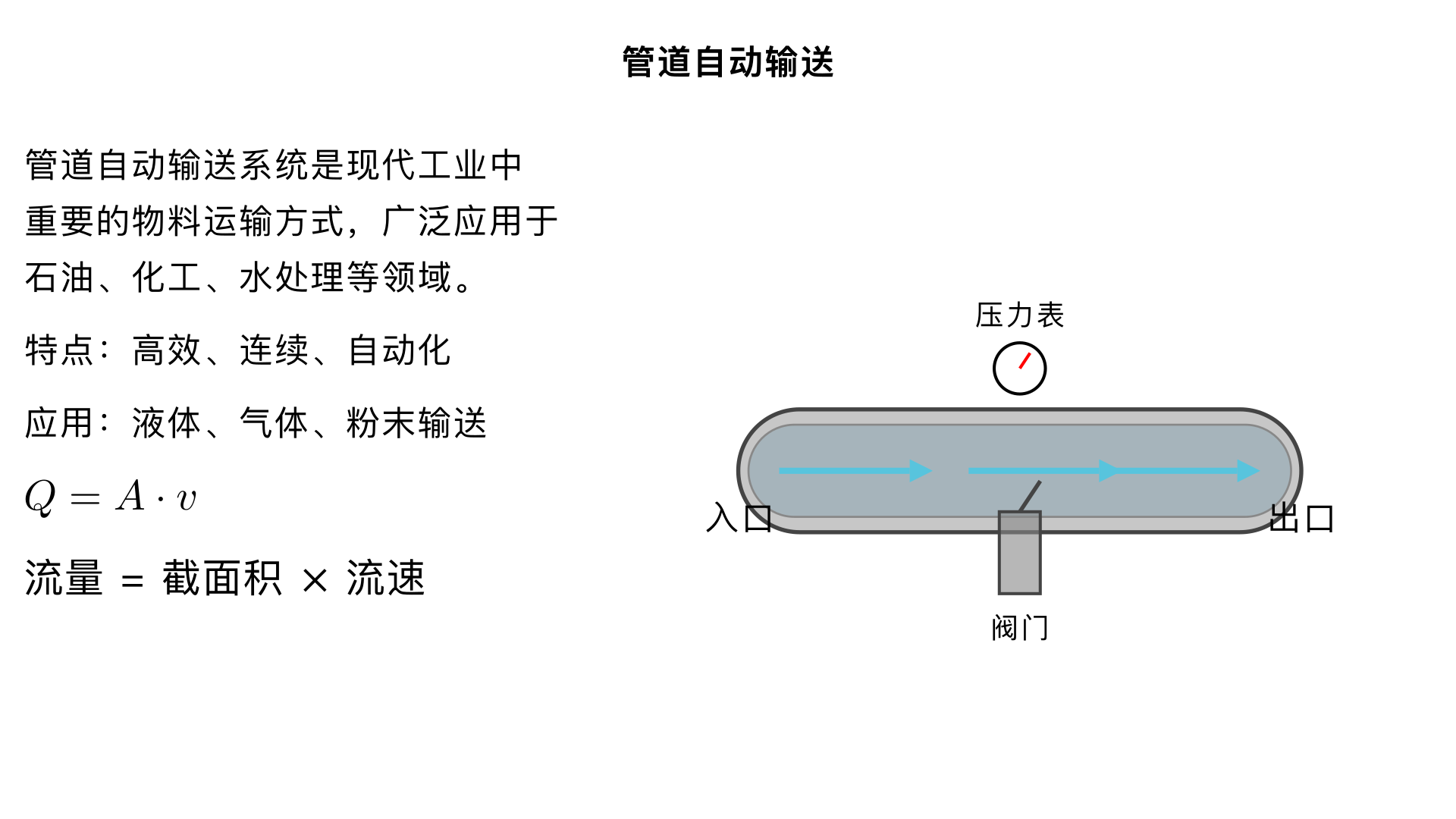
管道自动输送
▶
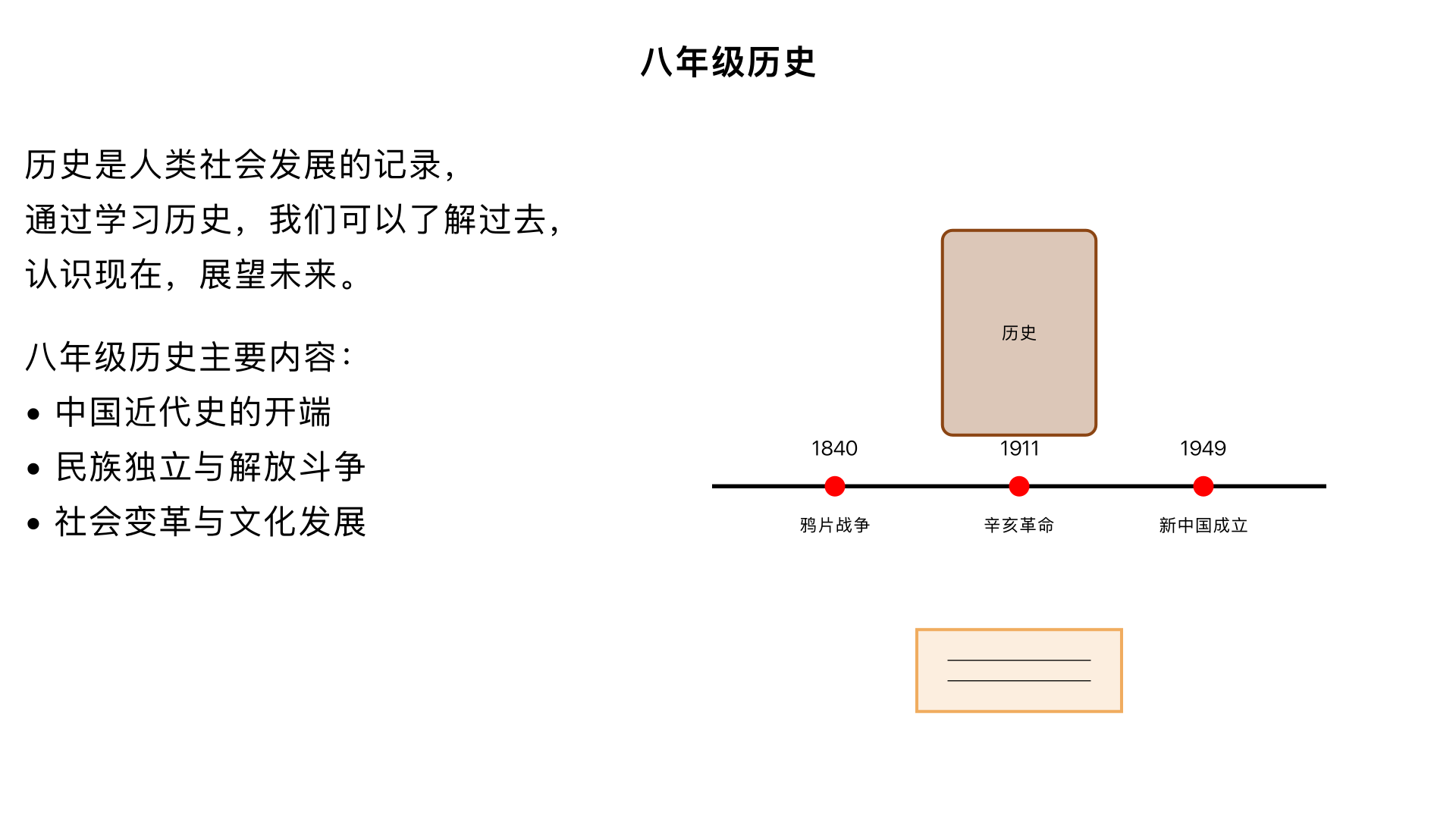
八年级历史
▶
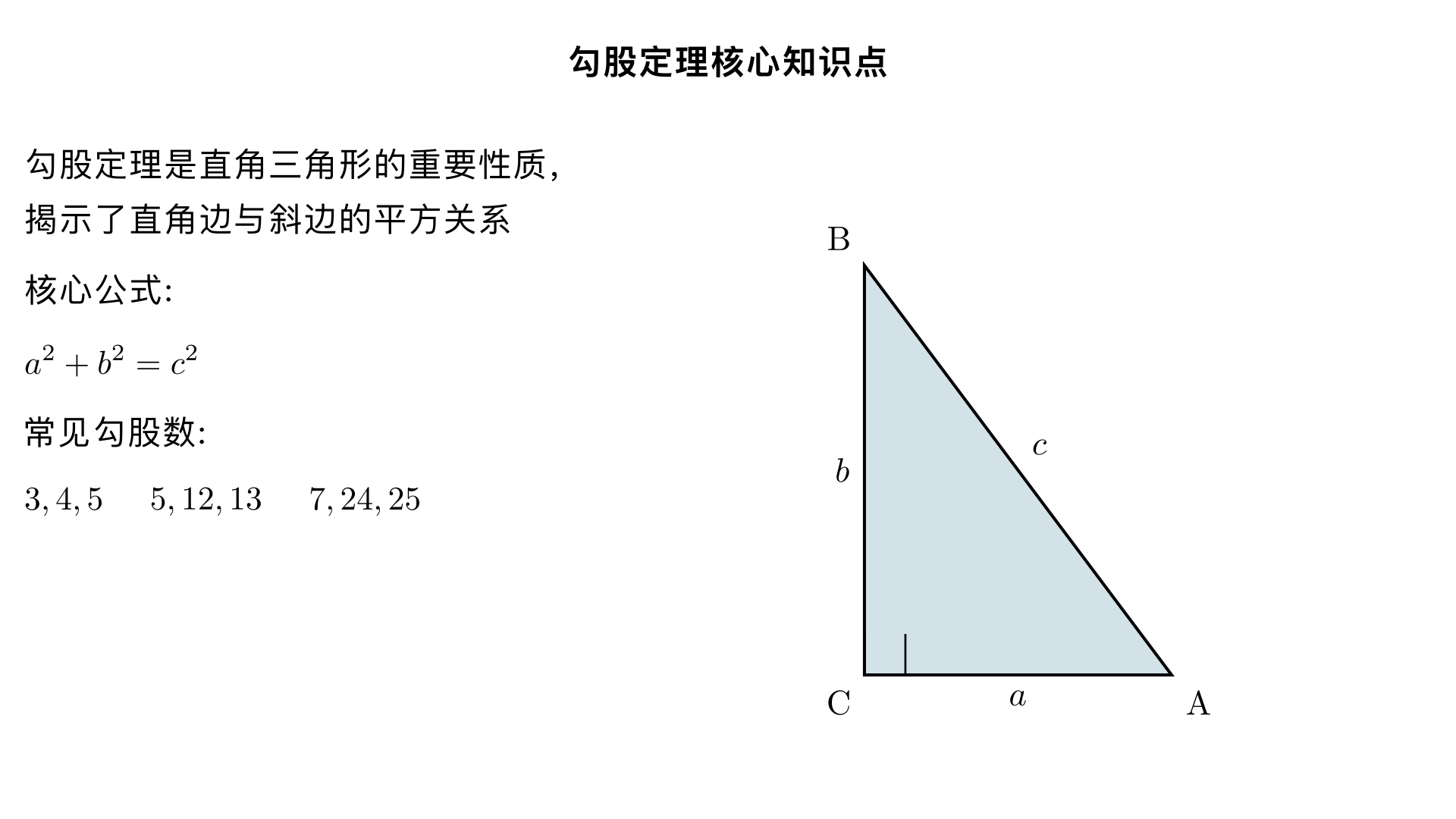
八年级数学 勾股定理 核心知识点(系统化拆解) 勾股定理是八年级几何的核心定理,也是直角三角形的重要性质,主要解决直角三角形的边长计算和线段平方关系证明问题,以下按定义→公式→验证→注意事项→常见勾股数→典型例题→解题步骤拆解,贴合八年级教材要求。 一、勾股定理的定义 在直角三角形中,两条直角边的平方和等于斜边的平方。 边的命名约定 设直角三角形的两条直角边长度分别为 a 、 b ,斜边(直角所对的边,最长边)长度为 c ,则勾股定理的核心表述围绕此三边展开。 二、核心公式及变形(必考) 1. 基本公式 a 2 +b 2 =c 2 (直角边 ² + 直角边 ² = 斜边 ²) 2. 常用变形公式(已知两边求第三边,直接套用) 求斜边: c= a 2 +b 2 求直角边 a : a= c 2 −b 2 求直角边 b : b= c 2 −a 2 ✅ 关键前提:仅适用于直角三角形,非直角三角形不能直接使用。 三、勾股定理的验证(教材重点,面积法核心) 勾股定理的验证本质是利用图形的面积相等推导,八年级要求掌握面积法,以下 3 种经典验证方法(赵爽弦图为必考): 1. 赵爽弦图(我国古代数学家赵爽证明,教材核心) 以直角三角形的斜边为边长作大正方形,内部用 4 个全等的直角三角形拼出小正方形,通过大正方形面积 = 4 个直角三角形面积 + 小正方形面积推导,是中考常考的证明素材。 2. 毕达哥拉斯证法 用两个全等的直角三角形拼出直角梯形,通过梯形面积 = 三个直角三角形面积和推导,核心仍是面积相等。 3. 总统证法(伽菲尔德证法) 与毕达哥拉斯证法思路一致,简化了梯形的拼接方式,步骤更简洁,适合八年级基础证明。 四、适用范围与核心注意事项(避错关键) 仅适用于直角三角形:锐角三角形、钝角三角形的三边不满足此关系; 斜边是前提:公式中 c 一定是斜边(最长边),若题目未明确边的类型,需分类讨论; 边长为正数:计算结果中,边长的算术平方根为正,舍去负根; 平方关系≠边长关系:注意区分 a 2 +b 2 =c 2 和 a+b=c ,后者一定不成立; 勾股定理是 “性质”:是已知直角三角形,推导三边平方关系,与后续 “勾股定理的逆定理(判定直角三角形)” 区分开。 五、常见勾股数(速算必备,八年级常考) 勾股数:满足 a 2 +b 2 =c 2 的正整数组 (a,b,c) ,核心勾股数及变形需熟记,解题可直接套用: 1. 基础勾股数(核心三组,必考) 3, 4, 5(最常用) 5, 12, 13 7, 24, 25 2. 勾股数的倍数性质 若 (a,b,c) 是勾股数,则其正整数倍 (ka,kb,kc) ( k>0 ,整数)也是勾股数,例如: 3,4,5 的 2 倍:6,8,10;3 倍:9,12,15 5,12,13 的 2 倍:10,24,26 ✅ 注意:1,2,3 不是勾股数( 1 2 +2 2 =3 2 ),勾股数需严格满足平方和关系。 六、典型例题(分类型,含解题步骤,贴合八年级考题) 勾股定理的考题分基础计算型、分类讨论型、实际应用型,是八年级同步练习的核心题型,以下各举一例,步骤按 “审题→定直角→标边→套公式” 展开。 类型 1:基础计算 —— 已知直角三角形两边,求第三边 例题:在 Rt△ABC 中,∠C=90°,若 a=3 , b=4 ,求斜边 c ;若 c=10 , a=6 ,求直角边 b 。解题步骤: 审题:∠C=90°,确定 c 为斜边, a,b 为直角边; 套公式: 求 c : c= 3 2 +4 2 = 25 =5 ; 求 b : b= 10 2 −6 2 = 64 =8 。 类型 2:分类讨论 —— 未明确 “斜边 / 直角边”,需分情况 例题:在 Rt△ABC 中,一条边长为 5,另一条边长为 12,求第三边的长。解题步骤: 审题:未明确直角边 / 斜边,第三边可能是斜边或直角边,分两种情况; 情况 1:12 为斜边,5 为直角边,第三边 x 为直角边: x= 12 2 −5 2 = 119 ; 情况 2:12 和 5 均为直角边,第三边 x 为斜边: x= 12 2 +5 2 =13 ; 结论:第三边长为 13 或 119 。 类型 3:实际应用 —— 将实际问题转化为 “直角三角形边长计算” 例题:一架长 10m 的梯子,斜靠在竖直的墙上,梯子底端离墙 6m,求梯子顶端到地面的高度。解题步骤: 转化:梯子为斜边(10m),底端离墙的距离为一条直角边(6m),顶端高度为另一条直角边(设为 h ); 套公式: h= 10 2 −6 2 =8 ; 结论:梯子顶端到地面的高度为 8m。 七、勾股定理核心解题步骤(通用) 无论基础题还是应用题,均遵循以下 4 步,可避免漏解、错解: 找直角:确定直角三角形的直角顶点,明确直角边和斜边(无直角则需构造直角,如折叠问题); 标边长:将已知边长标注在对应边上,未知边设为 x ; 套公式:根据勾股定理写等式,代入已知数; 算结果:求解方程,舍去负根(边长为正),有多种情况需分类讨论。

▶