T
Teach Me AnythingTMA
Video History
Page 11 / 43
▶
损与益——损益盈虚的辩证法则 一、损卦(山泽损):损下益上之道 1. 卦序背景与卦名释义 《序卦传》:“缓必有所失,故受之以损。” 损卦紧接解卦(缓解困难),提示缓解之后可能有所损失。 “损”字本义为减少,卦义为损下益上(减损下方以增益上方)。 2. 卦象分析:山泽损(䷨) 上艮山,下兑泽:山下有泽,泽卑山高,泽水减损以增山高。 卦爻结构:损卦由泰卦(䷊)变来:泰卦九三上行至上位,上六下行至三位(损下卦一阳,益上卦一阴),象征损下益上。 金景芳指出:损卦并非一味强调减损,而是“损所当损”,如损私益公、损己益人。 3. 《彖传》精解 text 损,损下益上,其道上行。 损而有孚,元吉,无咎,可贞,利有攸往。 曷之用?二簋可用享。 二簋应有时,损刚益柔有时。 损益盈虚,与时偕行。 “损下益上,其道上行”:点明损卦的基本性质,损下方之刚以益上方之柔。 “损而有孚”:减损必须心怀诚信,才能得“元吉、无咎、可贞、利有攸往”。 “二簋可用享”:用最简单的两簋食物即可祭祀,强调减损的诚意比形式重要。 “损刚益柔有时”:减损刚强、增益柔弱要适时而行。 “损益盈虚,与时偕行”:总结损益之道需顺应时势,这是全卦的核心思想。 4. 《大象传》:“山下有泽,损。君子以惩忿窒欲。” 君子观此卦象,要克制忿怒(惩忿)、抑制贪欲(窒欲),这是针对个人的减损修养。 5. 爻辞精析 初九:已事遄往,无咎,酌损之。 停下自己的事速去助人(损己益人),但应斟酌减损的程度。 九二:利贞,征凶,弗损益之。 利于守正,出征则凶;此时不应减损,也不应增益。 六三:三人行,则损一人;一人行,则得其友。 揭示阴阳相求的专一性:三人行(多则疑)则损一人,一人行(专一)则得友。 六四:损其疾,使遄有喜,无咎。 减损自己的疾病(错误),迅速改正则喜。 六五:或益之十朋之龟,弗克违,元吉。 有人进献价值十朋的宝龟(象征大助益),无法推辞,至为吉祥。 上九:弗损益之,无咎,贞吉,利有攸往,得臣无家。 不减损也不增益,得臣民拥戴而不分私家(大公无私)。 二、益卦(风雷益):损上益下之道 1. 卦序与卦名 《序卦传》:“损而不已必益,故受之以益。” 损极而益,体现物极必反。 益卦与损卦为综卦,象征损上益下(减损上方以增益下方)。 2. 卦象分析:风雷益(䷩) 上巽风,下震雷:风雷激荡,相互助益。 卦爻来源:益卦由否卦(䷋)变来:否卦九四下行至初位,初六上行至四位(损上卦一阳,益下卦一阴),象征损上益下。 金景芳强调:益卦体现“惠而不费”的施益智慧,强调自上而下的惠泽。 3. 《彖传》精解 text 益,损上益下,民说无疆。 自上下下,其道大光。 利有攸往,中正有庆。 利涉大川,木道乃行。 益动而巽,日进无疆。 天施地生,其益无方。 凡益之道,与时偕行。 “损上益下,民说无疆”:减损上层以增益下层,百姓无限欢悦。 “自上下下,其道大光”:从上施惠于下,其道光大。 “利有攸往,中正有庆”:指六二、九五皆中正,有吉庆。 “利涉大川,木道乃行”:巽为木,震为动,木舟动而可涉险。 “天施地生,其益无方”:天地施生万物,惠益无所不至。 “凡益之道,与时偕行”:与损卦一样,增益也要顺应时势。 4. 《大象传》:“风雷,益。君子以见善则迁,有过则改。” 君子见善则趋从(迁善),有过则改正,这是自我增益的修养。 5. 爻辞精析 初九:利用为大作,元吉,无咎。 利于大兴作,大吉无咎(因受益于上)。 六二:或益之十朋之龟,弗克违,永贞吉。王用享于帝,吉。 得重大助益,长久守正吉;王祭祀天帝,吉。 六三:益之用凶事,无咎。有孚中行,告公用圭。 增益用于救凶平险,无咎;心怀诚信、行中道,执圭告公(谨慎行事)。 六四:中行告公从,利用为依迁国。 行中道而告公,公必听从,利于依附迁徙国都(大事依从众议)。 九五:有孚惠心,勿问元吉。有孚惠我德。 有诚信惠人之心,不必问即知大吉;百姓也以诚信感惠我的恩德。 上九:莫益之,或击之,立心勿恒,凶。 无人增益他,有人攻击他;立心不恒常,凶险。 三、损益二卦的辩证关系总结 损与益的相互转化:损极而益,益极而损,构成循环。 政治哲学的启示: 损卦:损下益上需谨慎,强调“损而有孚”“与时偕行”。 益卦:损上益下得民心,但需“见善则迁,有过则改”。 个人修养的应用:惩忿窒欲(损)、迁善改过(益)。 金景芳总论:损益之道是治国理政与个人修身的重要法则,关键在于把握时机,当损则损,当益则益。
▶
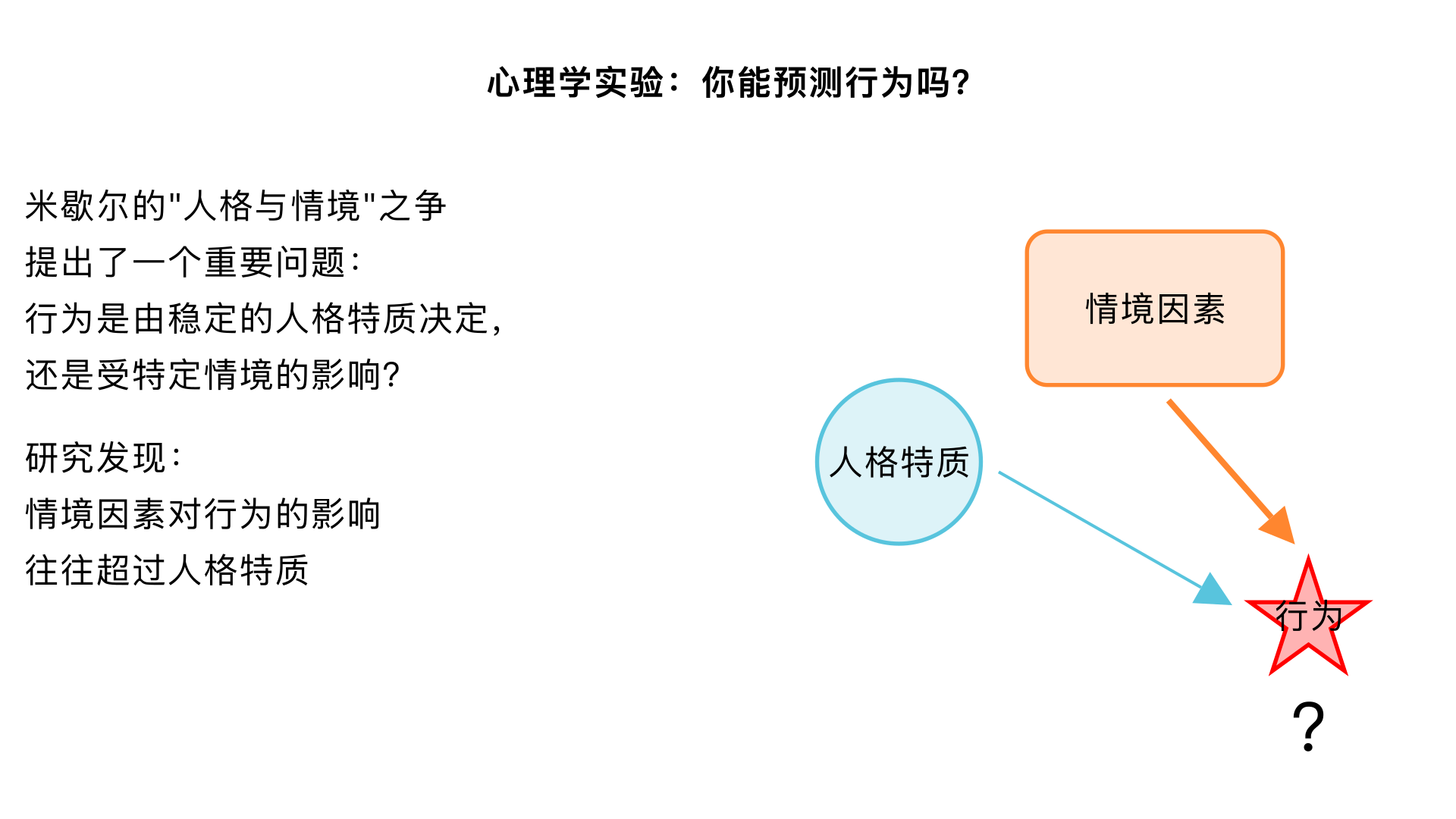
心理学实验:你能预测行为吗? (米歇尔的“人格与情境”之争) 主要内容:通过对大量研究的回顾,提出行为更多地受到特定情境的影响,而非稳定的人格特质。这一观点引发了人格心理学中著名的“人-情境之争”,促使研究者更深入地思考特质的边界条件。
▶
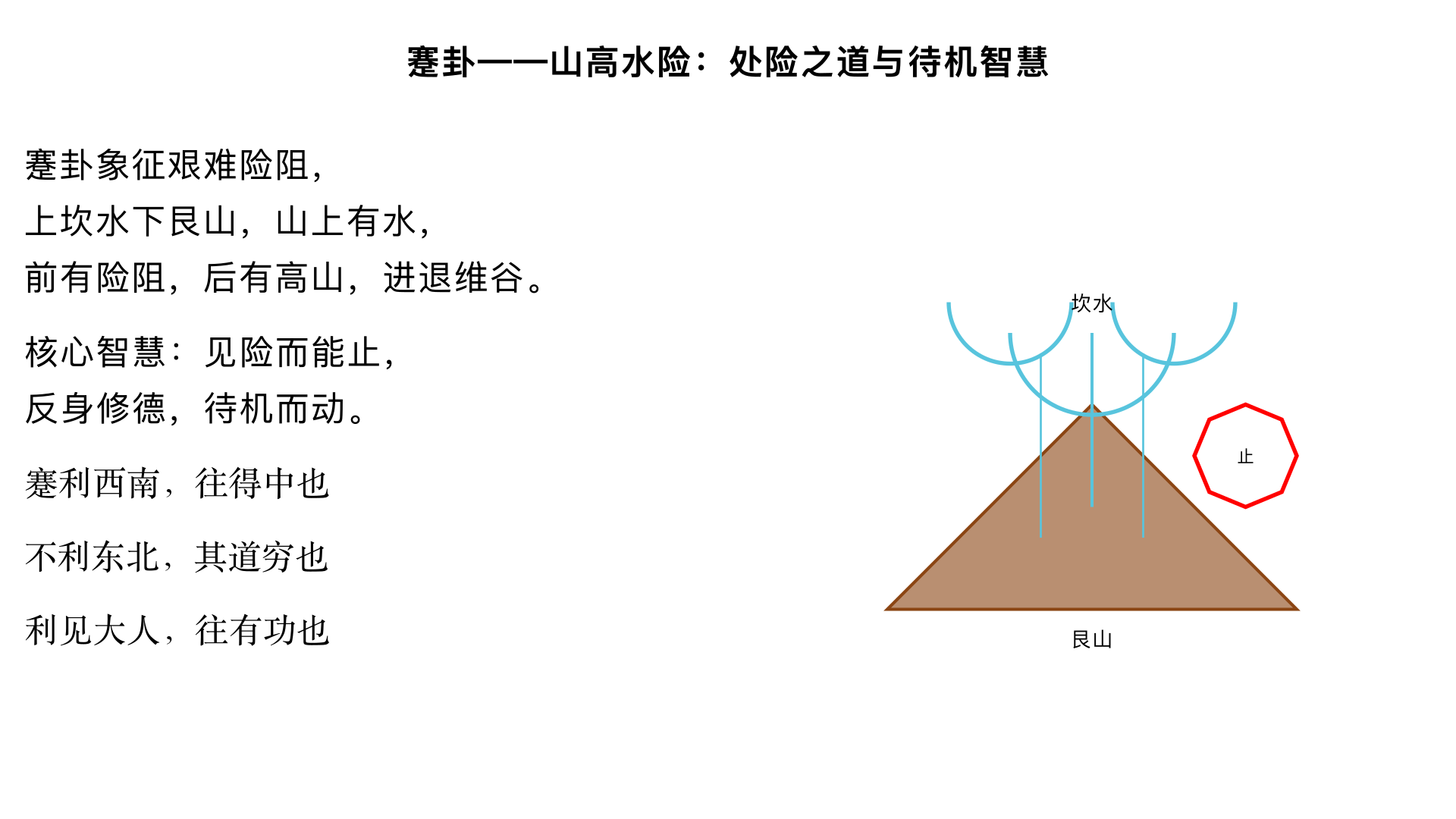
蹇卦——山高水险:处险之道与待机智慧 一、卦序背景:从睽违到艰难 1. 《序卦传》的逻辑 “睽者,乖也。乖必有难,故受之以蹇。蹇者,难也。” 睽卦(火泽睽)讲乖离、矛盾 → 矛盾激化则产生艰难 → 蹇卦(水山蹇)象征艰难险阻 金景芳指出:这是事物发展的必然链条,提示我们见睽当防蹇,及时化解矛盾避免艰难 2. 睽卦与蹇卦的象数关联 睽卦(䷥):上火下泽,二女同居,其志不同行 → 乖离 蹇卦(䷦):上坎下艮,山上有水,险阻在前 → 艰难 二卦互为综卦(蹇卦上下颠倒即睽卦),表明乖离与艰难是同一事物的两面 二、蹇卦(水山蹇)卦象的险阻之境 1. “山上有水”的自然险象 基本卦象:上坎水,下艮山 → 山上有水(瀑布、险流),或山高水险,行路艰难 自然象征: 水在山上:势能高,冲击力强,危险 山本止,水本险:止于险前,进退维谷 金景芳引申:此象可喻人生遇险,前有险阻(坎),后有高山(艮),难以行进 2. 卦德分析与应对原则 下艮为止,上坎为险 → 见险而能止 《彖传》:“蹇,难也,险在前也。见险而能止,知矣哉!” 核心智慧:知险而止,不是畏缩,而是明智的暂停,等待时机 3. 爻位结构中的希望 九五爻:阳刚中正居尊位,为“大人” 六二爻:柔顺中正,与九五正应 → 有应援 金景芳指出:虽处险境,但卦中有中正相应之爻,预示若得“大人”帮助,可济险难 三、彖传精解:处蹇之道 “蹇,难也,险在前也。见险而能止,知矣哉! 蹇利西南,往得中也;不利东北,其道穷也。 利见大人,往有功也。 当位贞吉,以正邦也。 蹇之时用大矣哉!” 1. “见险而能止,知矣哉!”的赞叹 知(智)的表现:不是盲目冒进,而是审时度势 历史例证:刘备被火烧连营后,退守白帝城,不再妄动,是“见险而能止” 反面教材:马谡不顾地势,扎营山上,被断水源,是“见险而不能止” 2. “蹇利西南,往得中也”的方位智慧 西南象征:坤方,平地,顺境(与坤卦“西南得朋”相呼应) “往得中”:前往西南可得中道(因九五居中) 金景芳考据:周族在岐山(东北),纣都在朝歌(西南),文王、武王向东南发展终得天下,是“利西南”的历史体现 3. “不利东北,其道穷也” 东北象征:艮方,山地,险境 “其道穷”:往东北则道途困穷 战略启示:避实就虚,不在艰难处硬碰 4. “利见大人,往有功也” “大人”:指九五,阳刚中正之君 “往有功”:往见大人则能建立功业 现实意义:处困境时,需寻找德才兼备的领导者或贵人 5. “当位贞吉,以正邦也” “当位”:卦中除初六外,其余五爻皆当位(阴居阴,阳居阳) “贞吉”:守正可获吉祥 “以正邦也”:可以端正邦国(即使处险,守正道仍可治国) 金景芳强调:蹇卦虽难,但爻多当位,提示在艰难中更要坚守本分 6. “蹇之时用大矣哉!”的赞叹 蹇卦的时用价值太重大了! 深层含义:艰难不是绝对的坏事,它可以磨砺人、考验人,成就事业 四、大象传:“反身修德”的内求智慧 “山上有水,蹇。君子以反身修德。” 1. “反身修德”四字精义 反身:反省自身,非怨天尤人 修德:修养德性,非向外求索 与《孟子》互证:“行有不得者,皆反求诸己” 2. 历史典范 周文王囚羑里:反身修德,演《周易》 苏轼贬黄州:反身修德,成《赤壁赋》 邓小平三起三落:反身修德,思考改革开放 3. 现代意义:企业危机时,领导者的自我反省与团队建设 五、爻辞精析:处险的六种境遇 蹇卦六爻展示了在不同位置、不同阶段面对艰难的策略,形成一个完整的处险智慧体系。 1. 初六:往蹇来誉。 爻象:初六阴柔居蹇始,上无应援(与六四同阴无应) “往蹇”:前进则遇艰难 “来誉”:退回来则得赞誉(因知止) 策略:力量微弱时,不宜冒进,知难而退是明智 案例:孔子“道不行,乘桴浮于海”,是“来誉” 2. 六二:王臣蹇蹇,匪躬之故。 “王臣蹇蹇”:君王的臣子陷入重重艰难 “匪躬之故”:不是由于自身的缘故(而是为君国) 爻位:六二柔顺中正,与九五君王正应 象征:忠臣为国赴难,鞠躬尽瘁 历史人物:诸葛亮“六出祁山”,是“王臣蹇蹇” 金景芳阐发:此爻体现儒家“为国赴难,义不容辞”的担当精神 3. 九三:往蹇来反。 “往蹇”:前进有险 “来反”:返回原处(反通返) 爻象:九三阳刚得位,处下卦之极,前进则遇坎险 应对:前有险阻,不如返回与初六、六二相守(下卦艮体,宜止) 战术启示:进攻受挫时,退回根据地,巩固基础 4. 六四:往蹇来连。 “往蹇”:前进艰难 “来连”:回来与九三相连(阴阳相合) 爻象:六四阴柔得正,已入坎体,但下与九三亲比 策略:身处险境,需与同志者联合 历史印证:刘备败退当阳,与关羽、张飞、赵云等“来连”,共抗曹操 5. 九五:大蹇朋来。 全卦主爻:处蹇之核心,最为艰难 “大蹇”:巨大的艰难 “朋来”:朋友前来相助 爻象:九五阳刚中正居尊,下应六二,且六四、上六皆来亲附 领袖智慧: 处大难时,因德行感召,得众人相助 如商汤被囚夏台,各方诸侯来救 金景芳强调:九五之“大蹇”是君主为天下承担的艰难,“朋来”是因德得助 6. 上六:往蹇来硕,吉。利见大人。 “往蹇”:前进仍艰难(处蹇极) “来硕”:回来则有大成就(硕,大也) “吉”:吉祥 “利见大人”:利于见九五大人 爻象:上六处蹇之终,前无去路,回归九五方为出路 含义:艰难至极时,回头依附有德领袖,可获大功 历史类比:韩信原从项羽,后“来硕”归刘邦,终成一代名将 六、蹇卦的处险智慧总论 1. 基本策略:“见险而能止” 不是消极避世,而是暂停观察,积蓄力量 2. 方向选择:“利西南,不利东北” 往平易方向(西南)发展,避艰险方向(东北) 3. 关键人物:“利见大人” 寻找德才兼备的领导者或贵人相助 4. 根本态度:“反身修德” 内求于己,修养德性,提高自身 5. 金景芳总结:蹇卦是儒家“处困而亨”思想的体现,强调在艰难中守正修德,待机而动。
▶
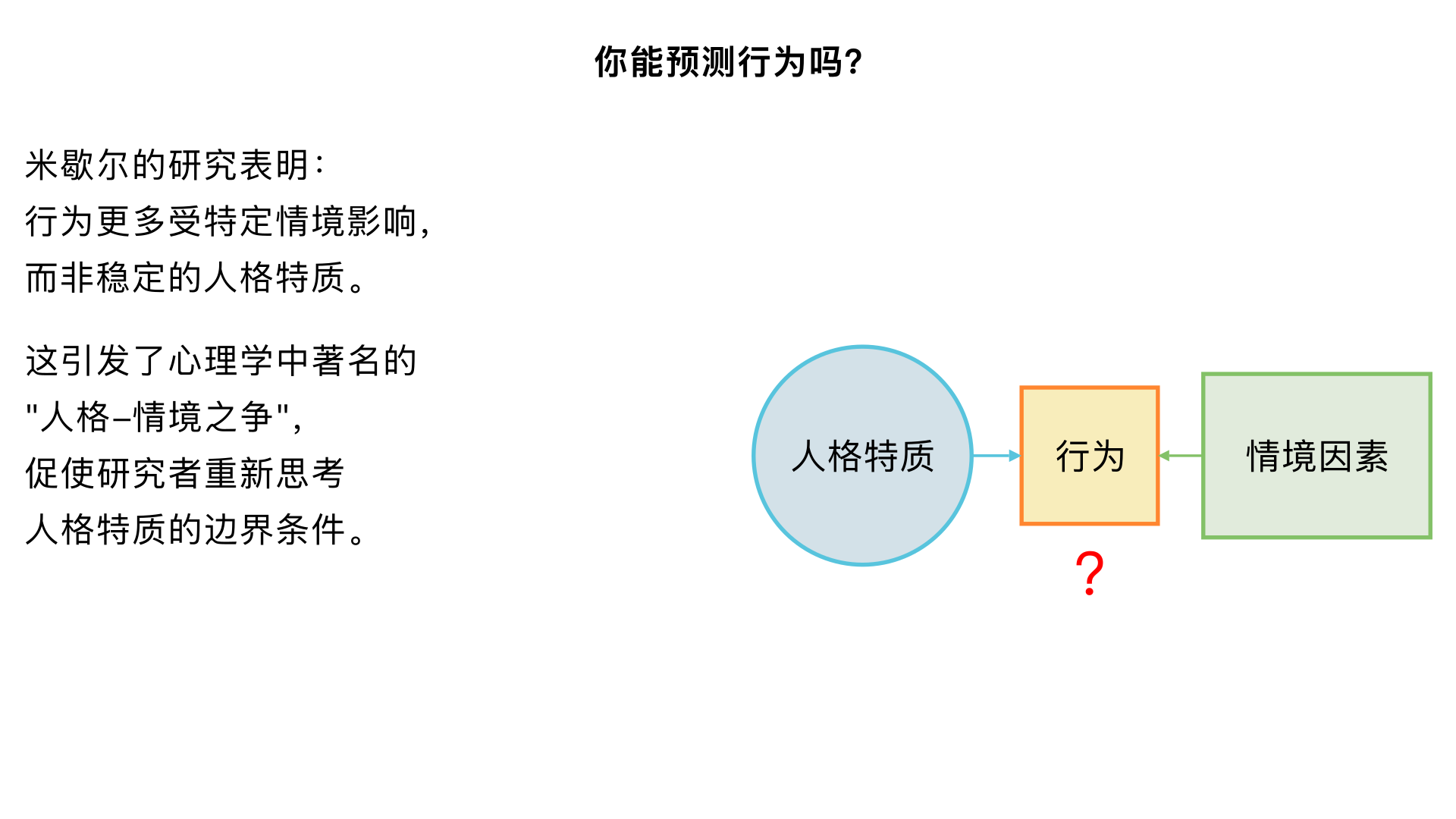
你能预测行为吗? (米歇尔的“人格与情境”之争) 主要内容:通过对大量研究的回顾,提出行为更多地受到特定情境的影响,而非稳定的人格特质。这一观点引发了人格心理学中著名的“人-情境之争”,促使研究者更深入地思考特质的边界条件。
▶
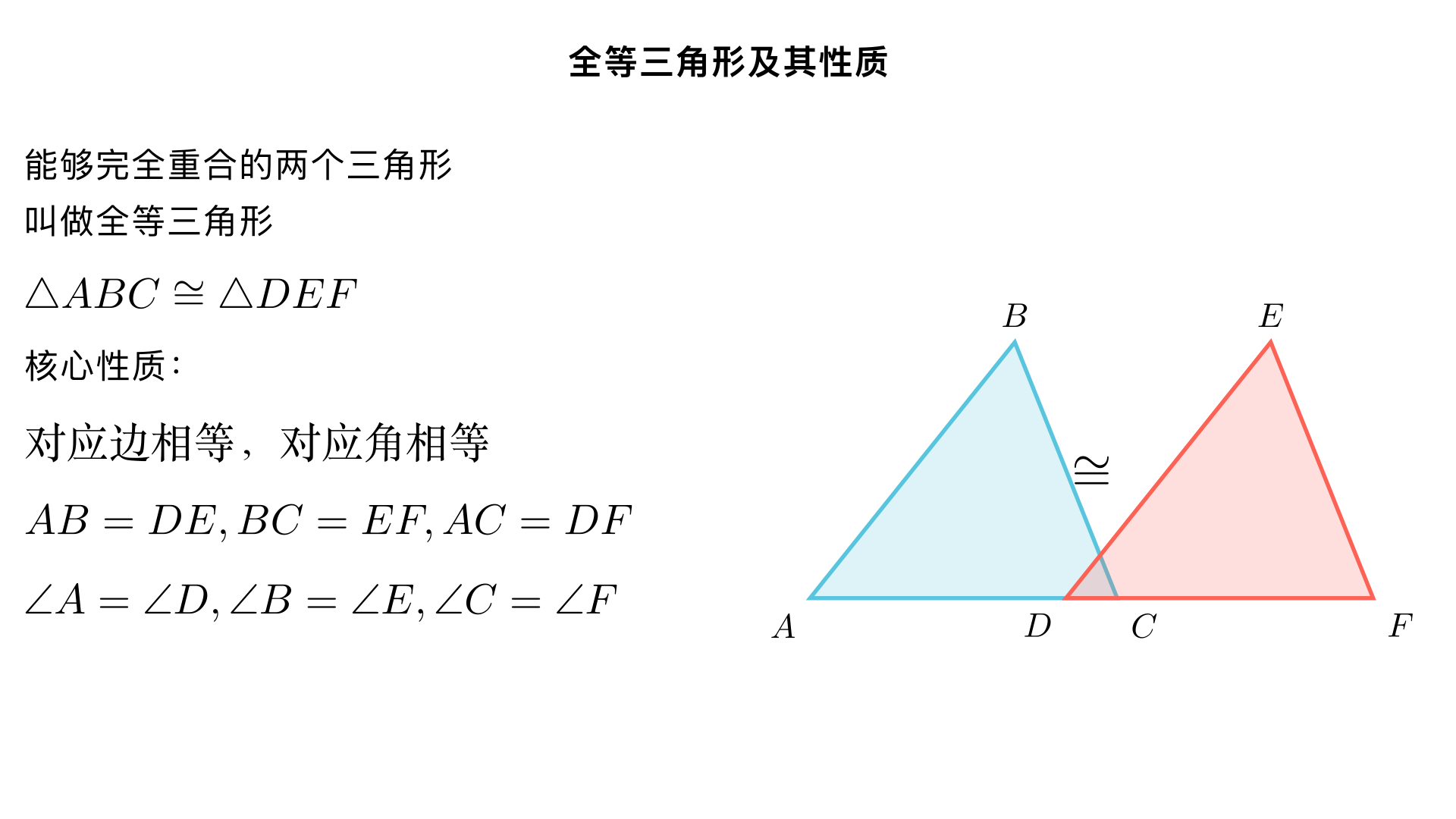
八年级数学 / 全等三角形 / 全等三角形及其性质 一、全等三角形的定义与表示方法 1. 定义 能够完全重合的两个三角形叫做全等三角形。 关键词:完全重合(形状相同 + 大小相等,二者缺一不可); 反例:形状相同但大小不同的两个三角形(如放大后的三角形与原三角形)、大小相同但形状不同的两个三角形(如一个锐角三角形和一个钝角三角形),都不是全等三角形。 2. 表示方法 用符号 “≌” 表示,读作 “全等于”。 书写规则:对应顶点必须写在对应位置上(这是后续找对应边、对应角的关键)。 例:若△ABC 和△DEF 完全重合,且 A 与 D、B 与 E、C 与 F 是对应顶点,则记作△ABC≌△DEF,读作 “△ABC 全等于△DEF”。 注意:不能写成△ABC≌△EDF(对应顶点顺序错误),否则会导致对应关系混乱。 3. 相关概念 全等三角形中,互相重合的顶点叫做对应顶点(如上述 A 与 D); 互相重合的边叫做对应边(如 AB 与 DE); 互相重合的角叫做对应角(如∠A 与∠D)。 二、全等三角形的对应关系找法(重点) 掌握对应关系是运用全等性质的前提,常见找法有 3 种: 根据顶点顺序找(最直接): 全等符号 “≌” 两侧的三角形,顶点按顺序一一对应(如△ABC≌△DEF,则 A↔D、B↔E、C↔F)。 根据图形特征找: 公共边是对应边(如两个三角形共用一条边,则这条边是对应边); 公共角、对顶角是对应角(如两个三角形有公共角,则公共角是对应角); 最长边对应最长边、最短边对应最短边;最大角对应最大角、最小角对应最小角。 根据图形变换找(结合平移、翻折、旋转): 平移得到的全等三角形:对应边平行(或在同一直线)、对应角相等(如将△ABC 沿水平方向平移得到△DEF,则 AB∥DE,∠A=∠D); 翻折得到的全等三角形:折痕是对应边的垂直平分线,对应角关于折痕对称(如将△ABC 沿直线 l 翻折得到△A'B'C',则折痕 l 垂直平分 AA',∠B=∠B'); 旋转得到的全等三角形:对应顶点到旋转中心的距离相等,对应角等于旋转角(如将△ABC 绕点 O 旋转 90° 得到△DEF,则 OA=OD,∠AOD=90°,∠C=∠F)。 三、全等三角形的性质(核心知识点) 全等三角形的核心性质:对应边相等,对应角相等(由 “完全重合” 直接推导,因为重合的边和角必然相等)。用符号语言表示(以△ABC≌△DEF 为例):∵ △ABC≌△DEF(已知),∴ AB=DE,BC=EF,AC=DF(全等三角形的对应边相等);∠A=∠D,∠B=∠E,∠C=∠F(全等三角形的对应角相等)。 延伸性质(由核心性质推导) 全等三角形的周长相等(对应边之和相等); 全等三角形的面积相等(形状、大小相同,面积必然相同); 全等三角形的对应边上的高、中线、角平分线相等
▶
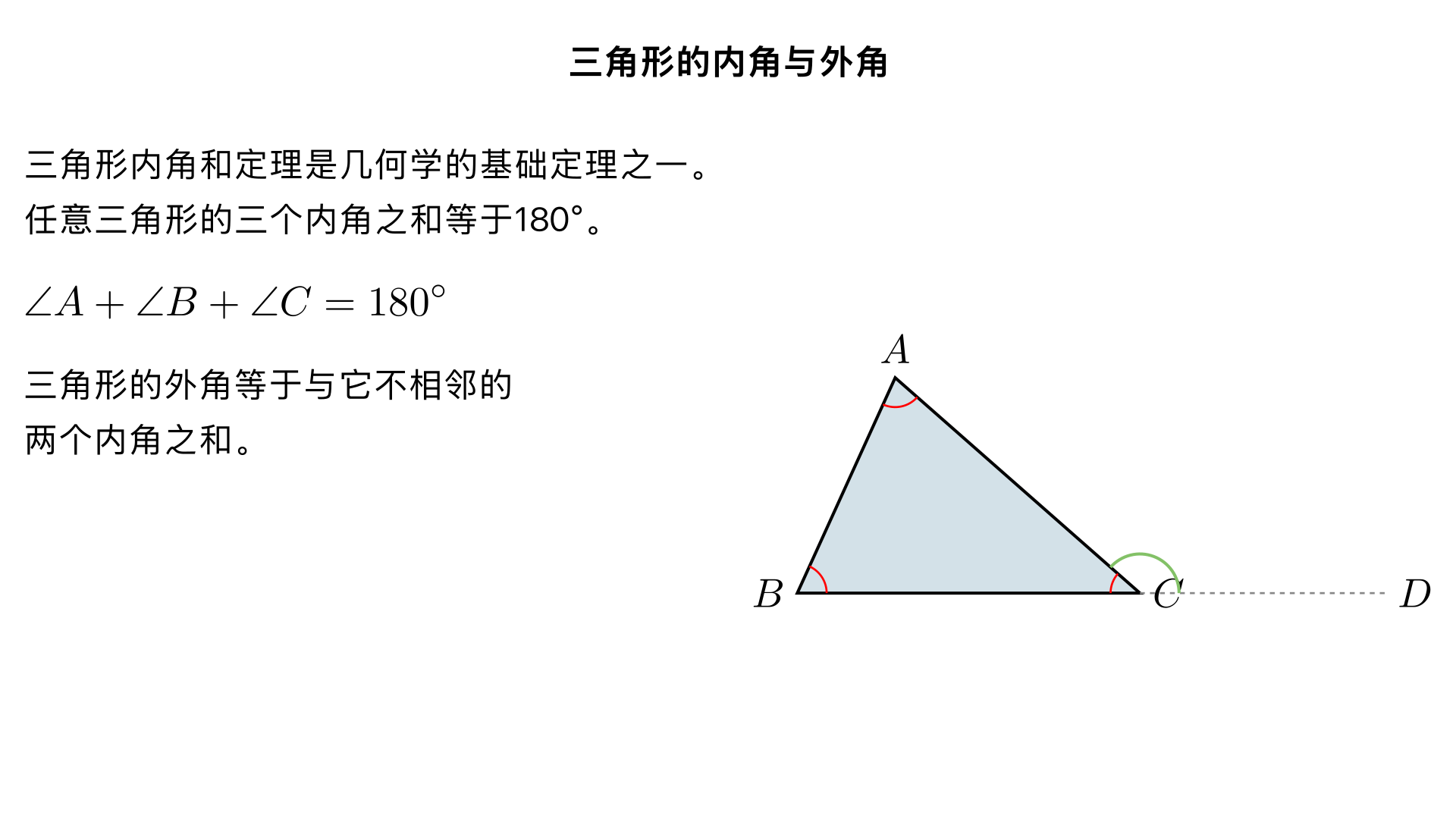
八年级数学 / 三角形 / 三角形的内角与外角 一、学习目标 掌握三角形内角和定理,能运用定理求三角形未知角的度数; 理解三角形外角的定义,熟记并灵活运用外角的三大性质; 掌握三角形外角和定理,能区分内角和与外角和的不同应用场景; 学会运用内角、外角相关知识解决几何计算与证明题,培养逻辑推理能力。 二、三角形的内角 2.1 核心定理:三角形内角和定理 内容:任意三角形的三个内角的和等于 180 ∘ (即 ∠A+∠B+∠C=180 ∘ ,其中 、 、 为三角形的三个内角)。 2.2 定理证明(3 种常用方法,易懂且必考) 方法 1:剪拼法(直观验证,适合理解) 步骤:将三角形的三个内角剪下,把顶点重合拼在一起,可发现三个角恰好组成一个平角(平角为 180 ∘ )。 注意:这是验证方法,不能作为严格证明,考试需用几何推理方法。 方法 2:作平行线法(教材重点,必考证明思路) 已知: △ABC ,求证: ∠A+∠B+∠ACB=180 ∘ 证明: 过点 C 作直线 DE∥AB (辅助线:作平行线,标注 “ DE∥AB ”); 由平行线性质: ∠A=∠ACD (内错角相等), ∠B=∠BCE (内错角相等); 因为 、 、 在同一直线上,所以 ∠ACD+∠ACB+∠BCE=180 ∘ (平角定义); 等量代换得: ∠A+∠B+∠ACB=180 ∘ 。 方法 3:延长线段法(辅助线另一种常见形式) 步骤:延长 BC 至点 D ,过点 C 作 CE∥AB ; 利用平行线性质: ∠A=∠ACE (内错角), ∠B=∠ECD (同位角); 平角 ∠BCD=180 ∘ ,即 ∠ACB+∠ACE+∠ECD=180 ∘ ,等量代换得内角和为 180 ∘
▶
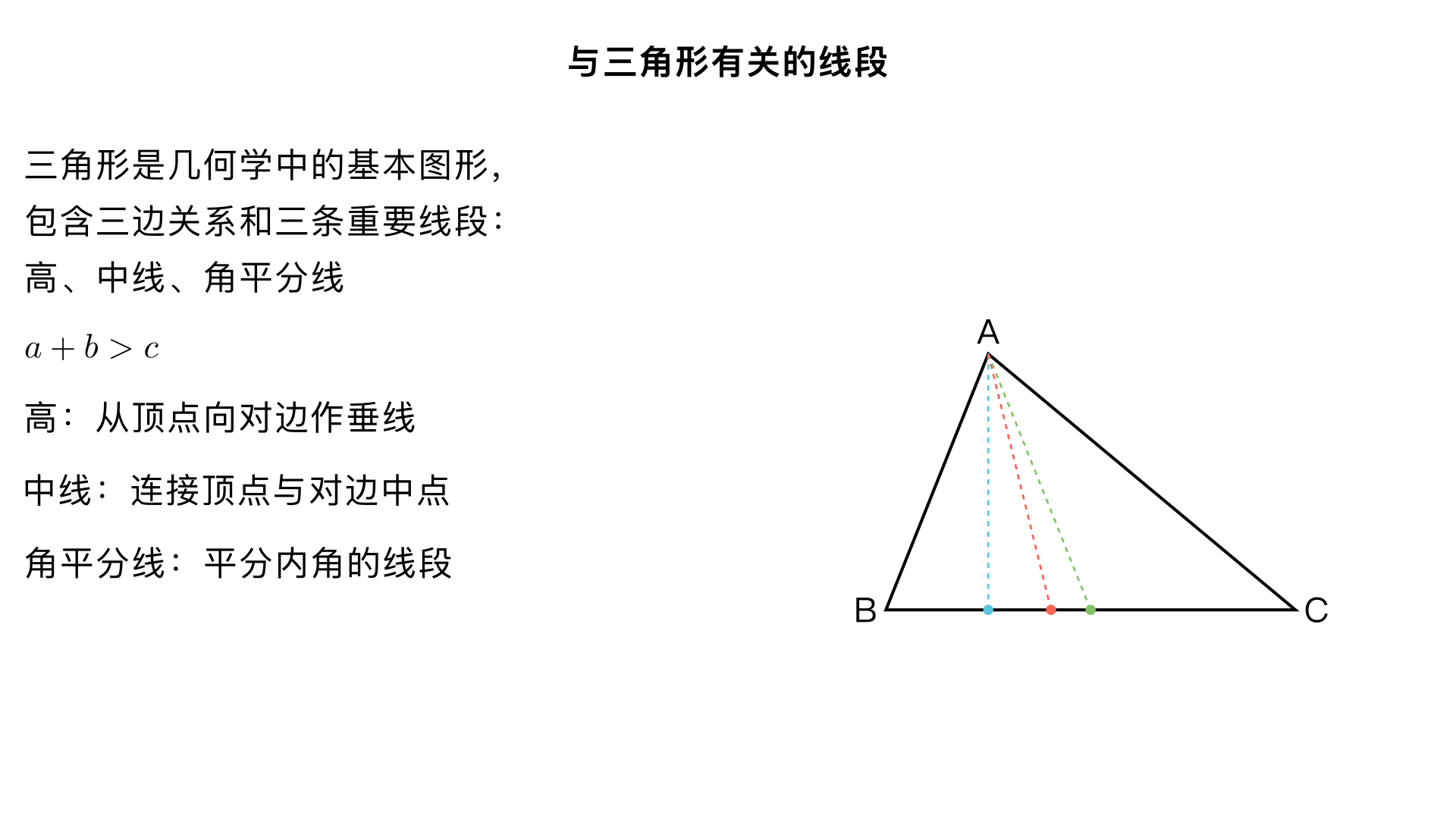
八年级数学:与三角形有关的线段 一、三角形的三边关系 定理:三角形任意两边之和大于第三边;任意两边之差小于第三边。 数学表达: 若三角形三边为 a, b, c,则: a + b > c b + c > a a + c > b |a - b| < c |b - c| < a |a - c| < b 应用:判断三条线段能否组成三角形(只需验证:两条较短线段之和 > 最长线段)。 原理:两点之间线段最短。 二、三角形的三条重要线段 1. 三角形的高 定义:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高。 几何表示:在△ABC 中,AD⊥BC 于 D,则 AD 是 BC 边上的高。 特点: 三角形有三条高(每边对应一条) 锐角三角形:三条高都在三角形内部 直角三角形:两条高是直角边,一条在内部 钝角三角形:两条高在外部,一条在内部 作用:计算三角形面积(S = 1/2 × 底 × 高) 2. 三角形的中线 定义:连接三角形一个顶点和它对边中点的线段叫做三角形的中线。 几何表示:在△ABC 中,E 是 BC 的中点,则 AE 是 BC 边上的中线。 特点: 三角形有三条中线,都在三角形内部 三条中线交于一点,称为三角形的重心 重心到顶点的距离是到对边中点距离的 2 倍 性质: 中线将三角形分成面积相等的两个小三角形 3. 三角形的角平分线 定义:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。 几何表示:在△ABC 中,∠BAD = ∠CAD,则 AD 是∠BAC 的角平分线。 特点: 三角形有三条角平分线,都在三角形内部 三条角平分线交于一点,称为三角形的内心(内切圆圆心)
▶
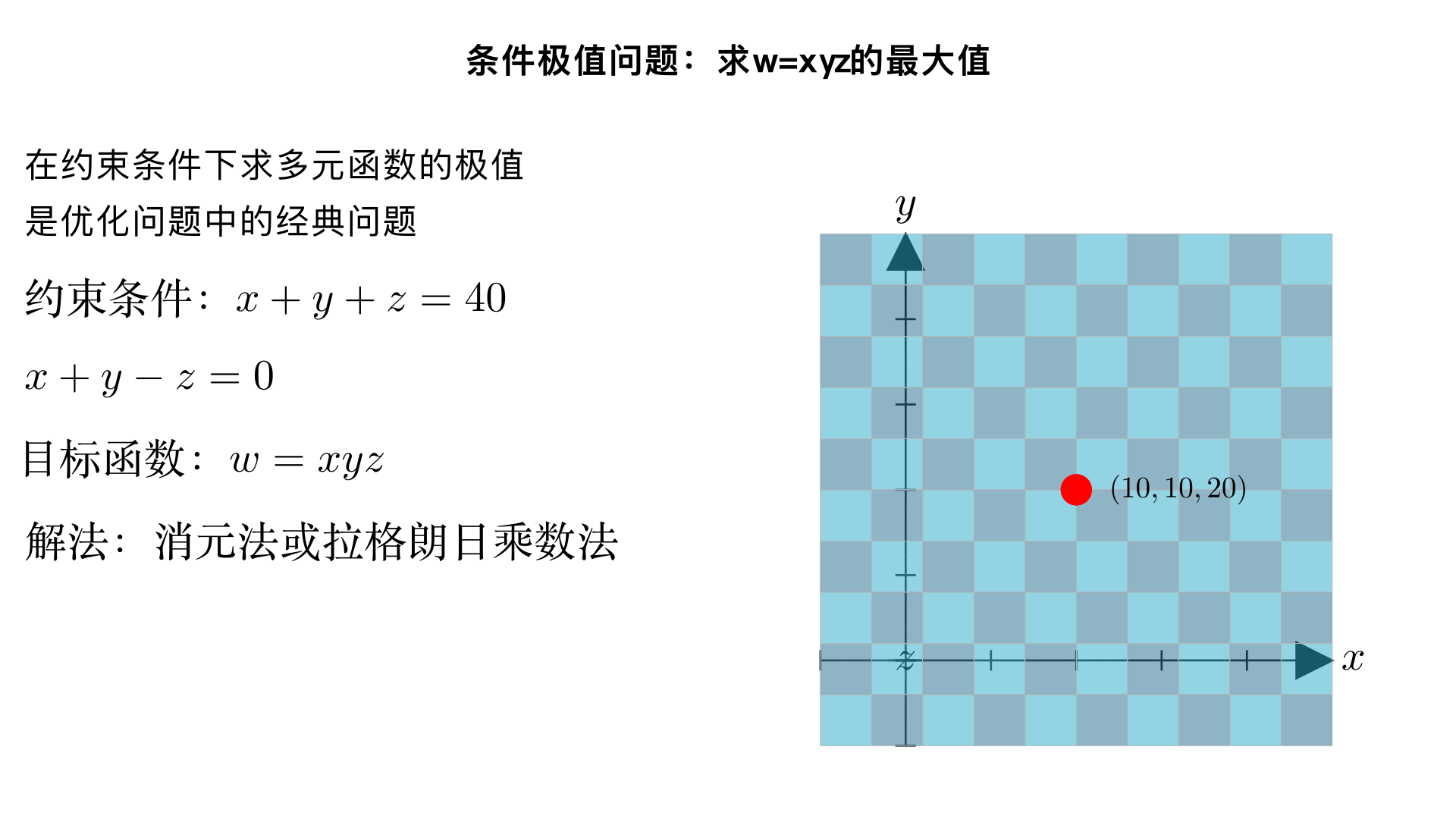
find the maximum value of w=xyz on x+y+z=40 and x+y-z=0
▶
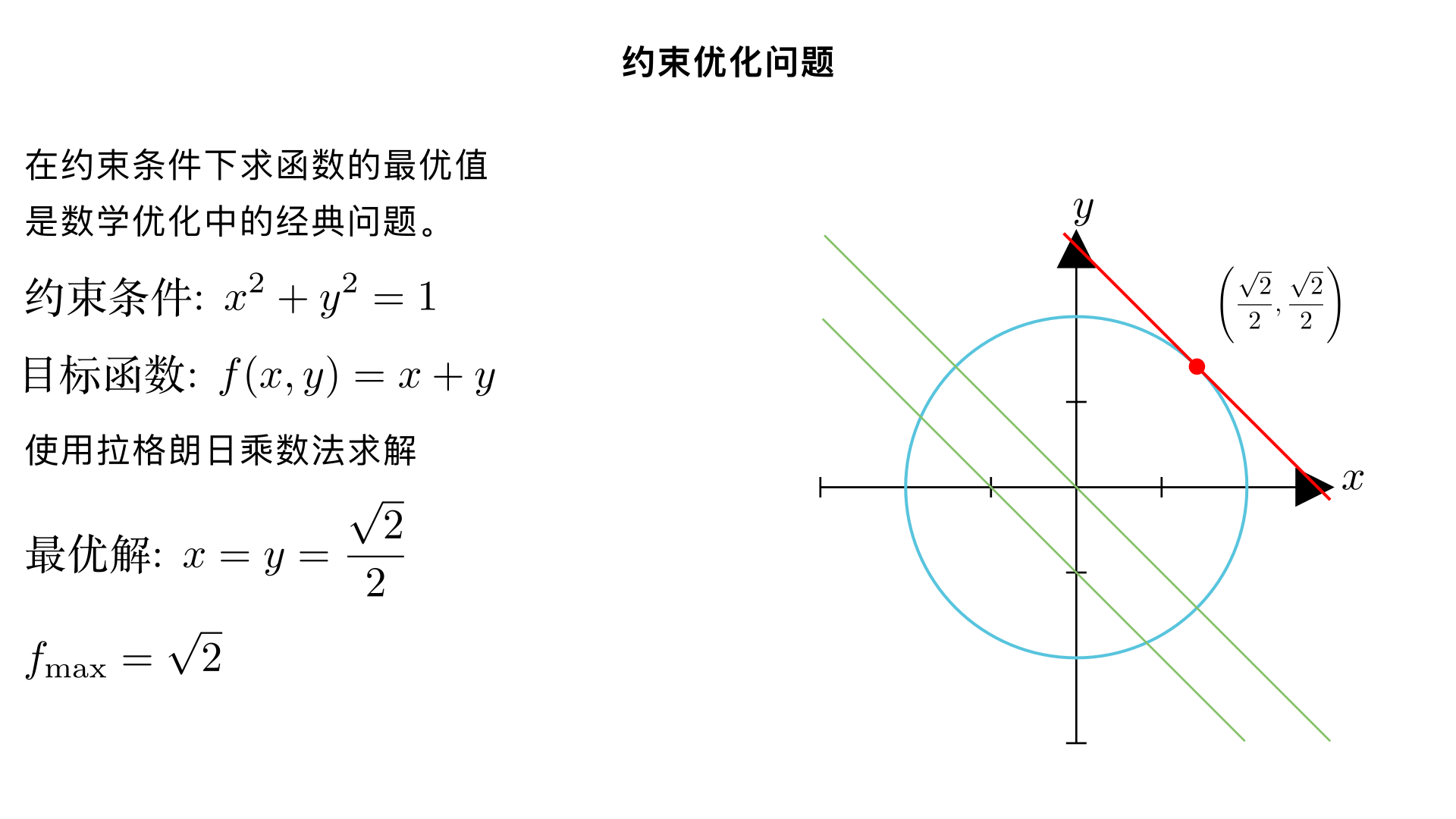
约束 x^2+y^2=1,优化 f(x,y)=x+y
▶
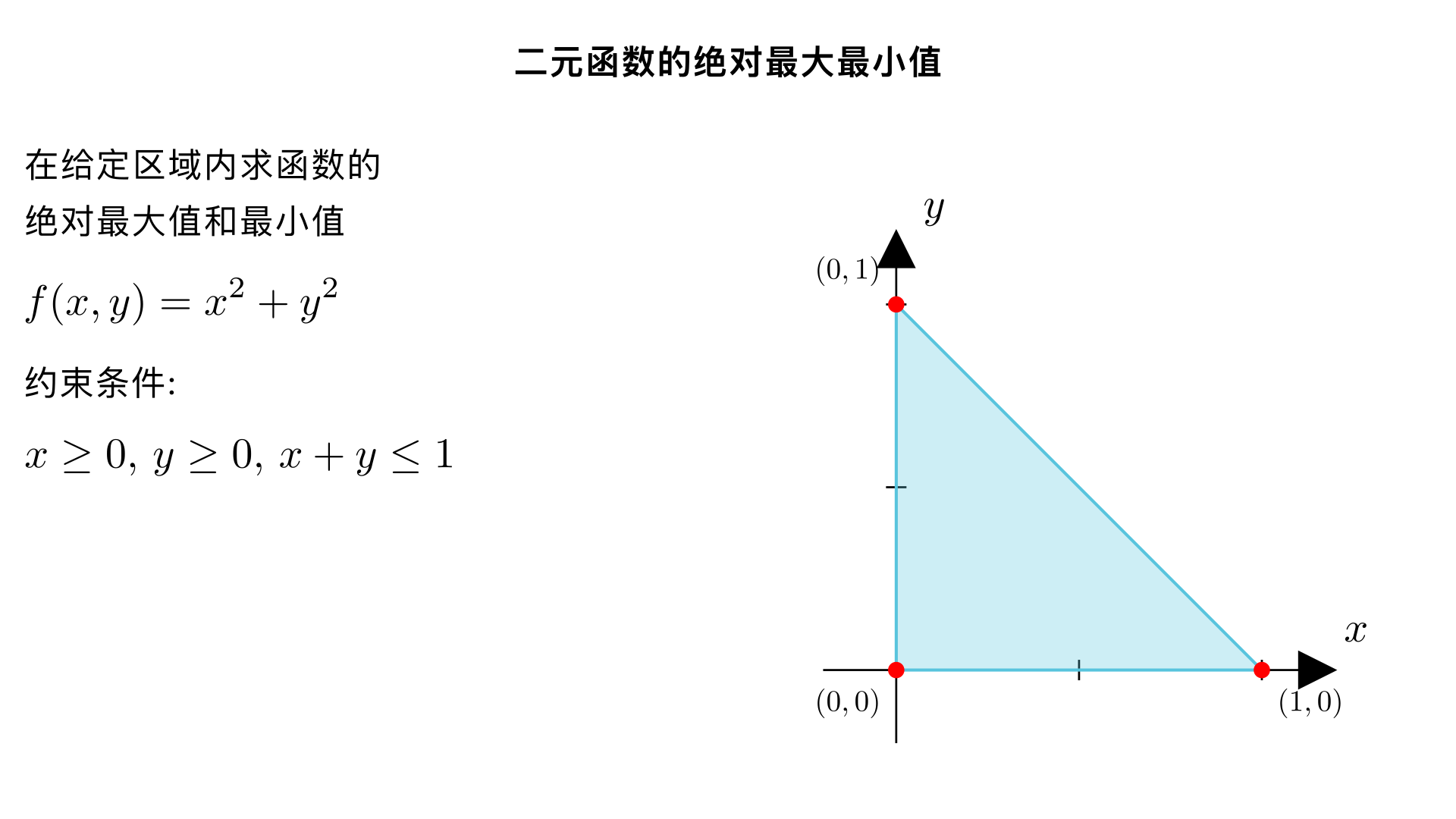
f(x,y)=x^2+y^2,区域x≥0, y≥0, x+y≤1。求绝对最大/最小。
▶
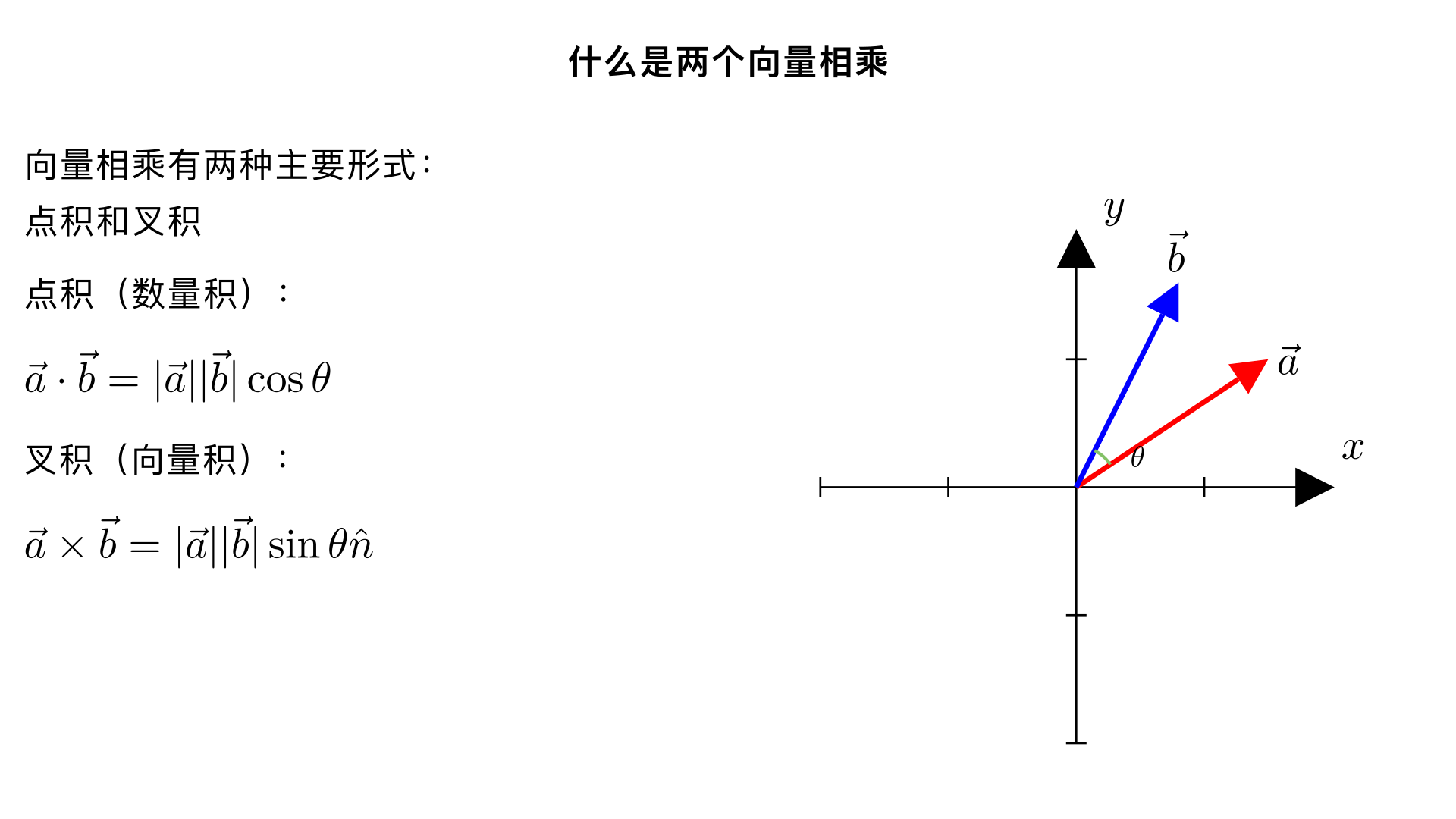
什么是两个向量相乘
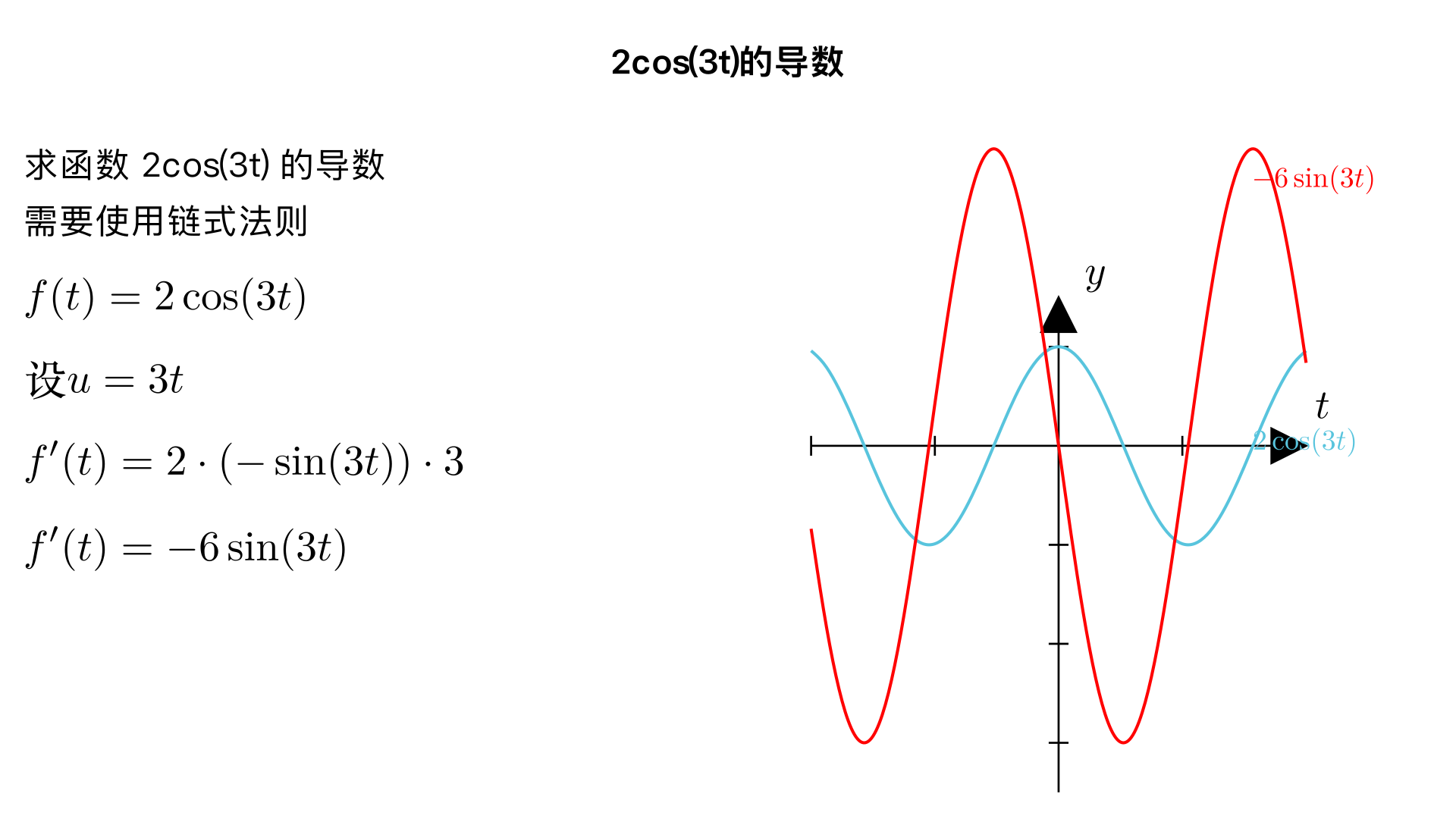
▶