T
Teach Me AnythingTMA
Video History
Page 12 / 43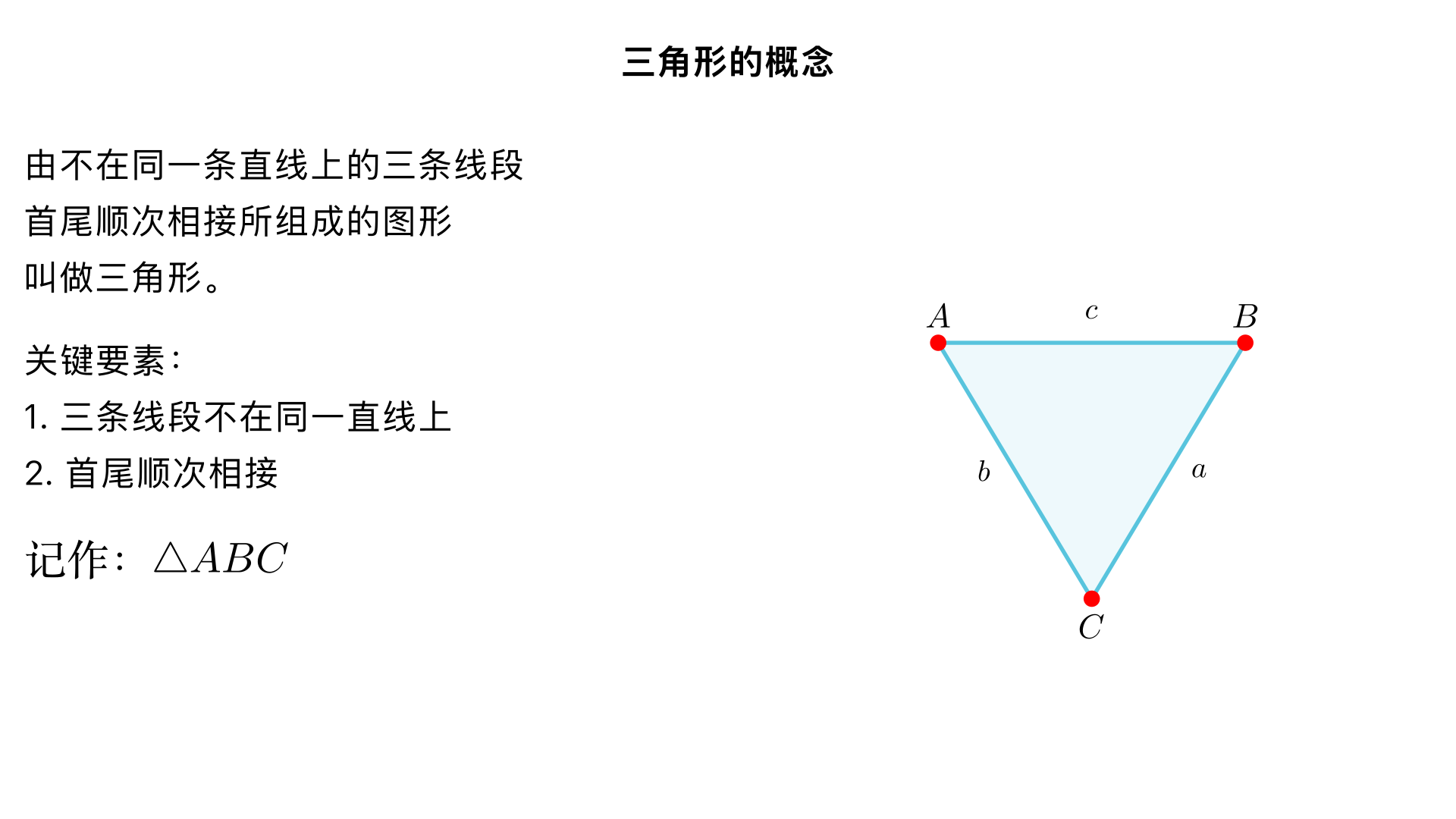
▶
八年级数学 / 三角形 / 用三角形的概念 一、核心概念(基础必备) 1. 三角形的定义 由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。 关键词:不在同一直线、首尾顺次相接(缺一不可,若三条线段共线或未首尾相连,均不构成三角形)。 图形表示:顶点用大写字母表示(如 A、B、C),三角形记作△ABC,读作 “三角形 ABC”。
▶
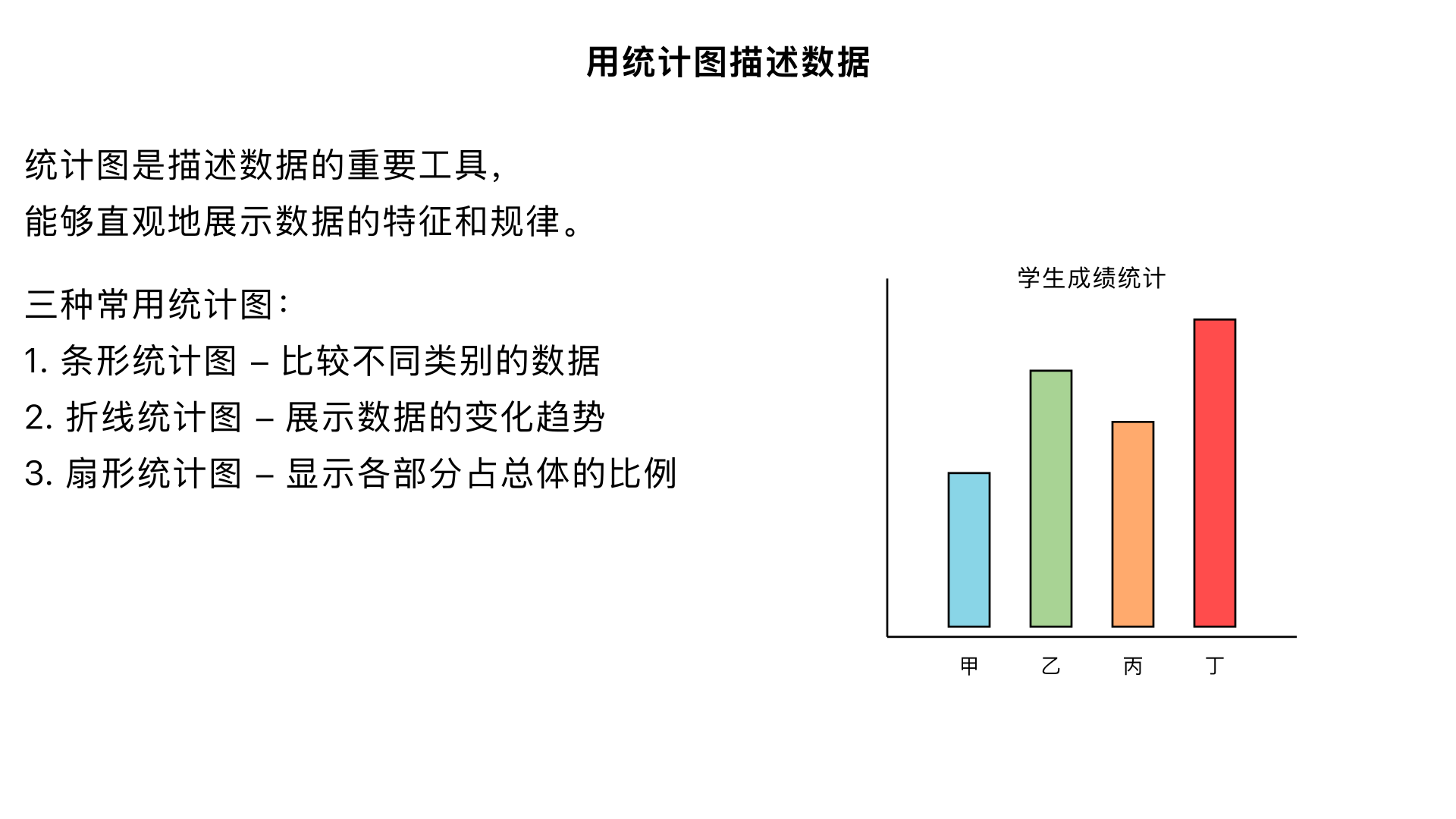
七年级数学 / 数据的收集、整理与描述 / 用统计图描述数据 一、核心目标 掌握三种常用统计图(条形统计图、折线统计图、扇形统计图)的定义、特点及适用场景; 学会根据数据类型和分析需求选择合适的统计图; 能规范绘制简单的条形统计图和折线统计图,理解扇形统计图的绘制原理; 能从统计图中准确提取有效信息,进行简单的数据分析。
▶
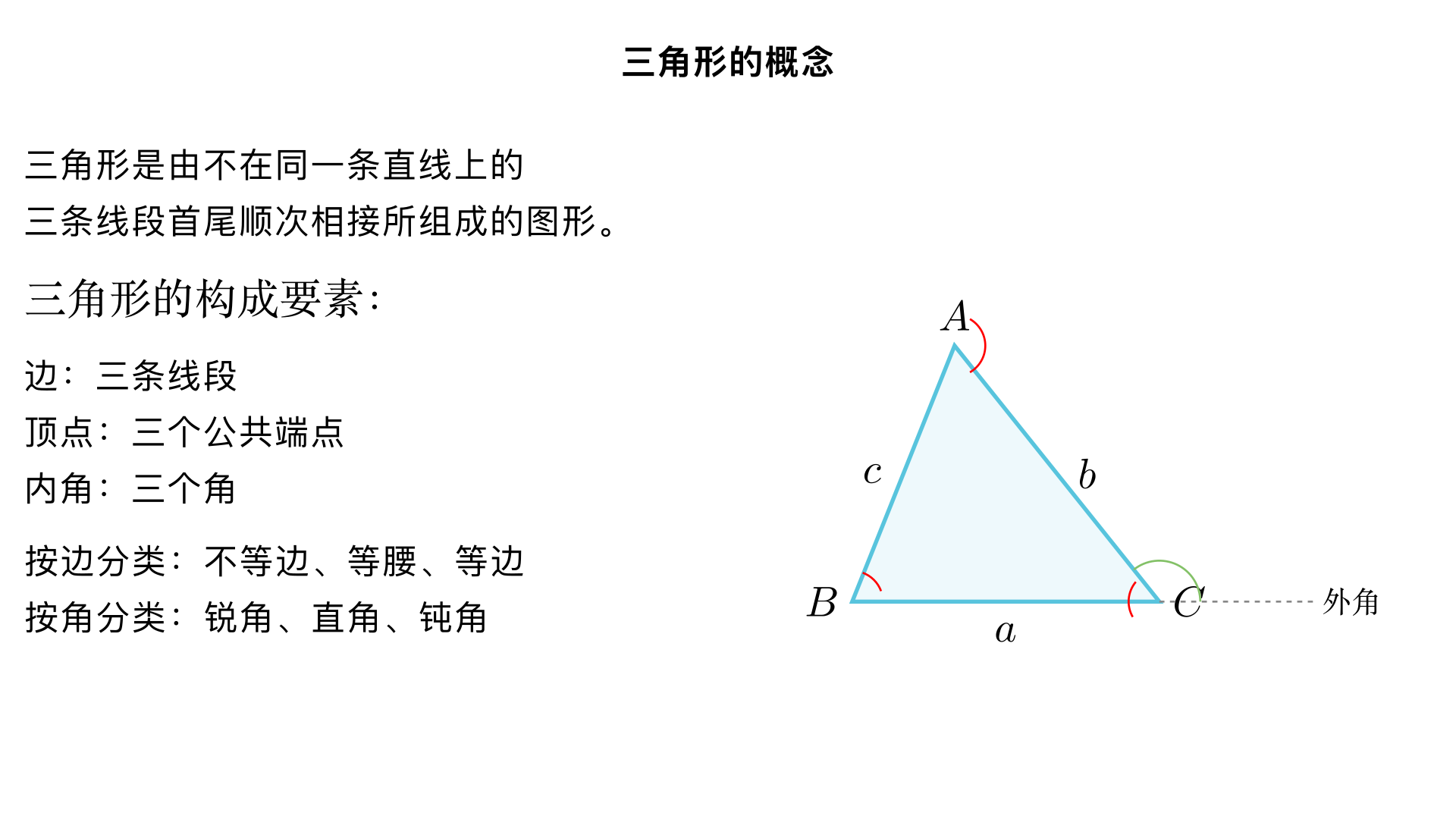
八年级数学 / 三角形 / 用三角形的概念 一、核心概念(基础必备) 1. 三角形的定义 由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。 关键词:不在同一直线、首尾顺次相接(缺一不可,若三条线段共线或未首尾相连,均不构成三角形)。 图形表示:顶点用大写字母表示(如 A、B、C),三角形记作△ABC,读作 “三角形 ABC”。 2. 三角形的构成要素 要素 定义 / 说明 表示方式 边 组成三角形的三条线段 边 AB、边 BC、边 AC(或 a、b、c,通常 a 对应 BC,b 对应 AC,c 对应 AB) 顶点 三条线段的公共端点 顶点 A、顶点 B、顶点 C 内角(简称角) 三角形相邻两边组成的角(共 3 个,且内角和为 180°,后续重点学习) ∠A、∠B、∠C(对应顶点命名) 外角 三角形的一边与另一边的延长线组成的角(共 6 个,每个内角对应 2 个外角) 如∠ACD(△ABC 中,边 BC 延长至 D,∠ACD 为∠C 的外角) 3. 三角形的表示与书写规范 记作△ABC(顶点字母无顺序要求,可写作△BAC、△ACB 等); 边的表示:可写 “边 AB” 或直接用小写字母 “c”(对应顶点 C 的对边); 角的表示:单个角用顶点字母(如∠A),若同一顶点有多个角,需用三个字母(如∠BAD,避免歧义)。 二、三角形的分类(按概念属性划分) 1. 按边的关系分类 类型 定义 关键特征 图形示意(文字描述) 不等边三角形 三条边都不相等的三角形 三边长度均不同(a≠b≠c) 三条边长度差异明显 等腰三角形 至少有两条边相等的三角形 有 “腰” 和 “底”:相等的两边为腰,第三边为底;两腰的夹角为顶角,腰与底的夹角为底角 两条边长度相同,一条不同 等边三角形 三条边都相等的三角形(特殊的等腰三角形) 三边相等(a=b=c),三个内角均为 60° 三条边长度完全相同 注意:等边三角形是等腰三角形的 “特殊情况”(满足 “至少两条边相等”),但等腰三角形不一定是等边三角形。 2. 按角的大小分类 类型 定义 关键特征 图形示意(文字描述) 锐角三角形 三个内角都是锐角(小于 90°)的三角形 三个角均<90° 三个角都比较 “尖” 直角三角形 有一个内角是直角(等于 90°)的三角形 有一个角 = 90°,另外两个角为锐角(和为 90°);直角所对的边为斜边(最长边),另外两条边为直角边 有一个角是 “直角符号” 钝角三角形 有一个内角是钝角(大于 90° 且小于 180°)的三角形 有一个角在 90°~180° 之间,另外两个角为锐角 有一个角比较 “钝” 注意:三角形中最多只有一个直角或钝角(因为内角和为 180°,若有两个直角 / 钝角,内角和会超过 180°)。 三、三角形概念的核心应用(必练题型) 题型 1:判断是否为三角形(依据定义 + 三边关系) 解题关键: 先看三条线段是否 “不在同一直线”(题目未说明时,默认不共线); 再验证 “首尾顺次相接”(几何图形题中,若线段端点相连,即满足); 补充:三角形三边关系(后续重点,但概念应用中需初步掌握)——任意两边之和大于第三边,任意两边之差小于第三边(不满足则无法构成三角形)。
▶
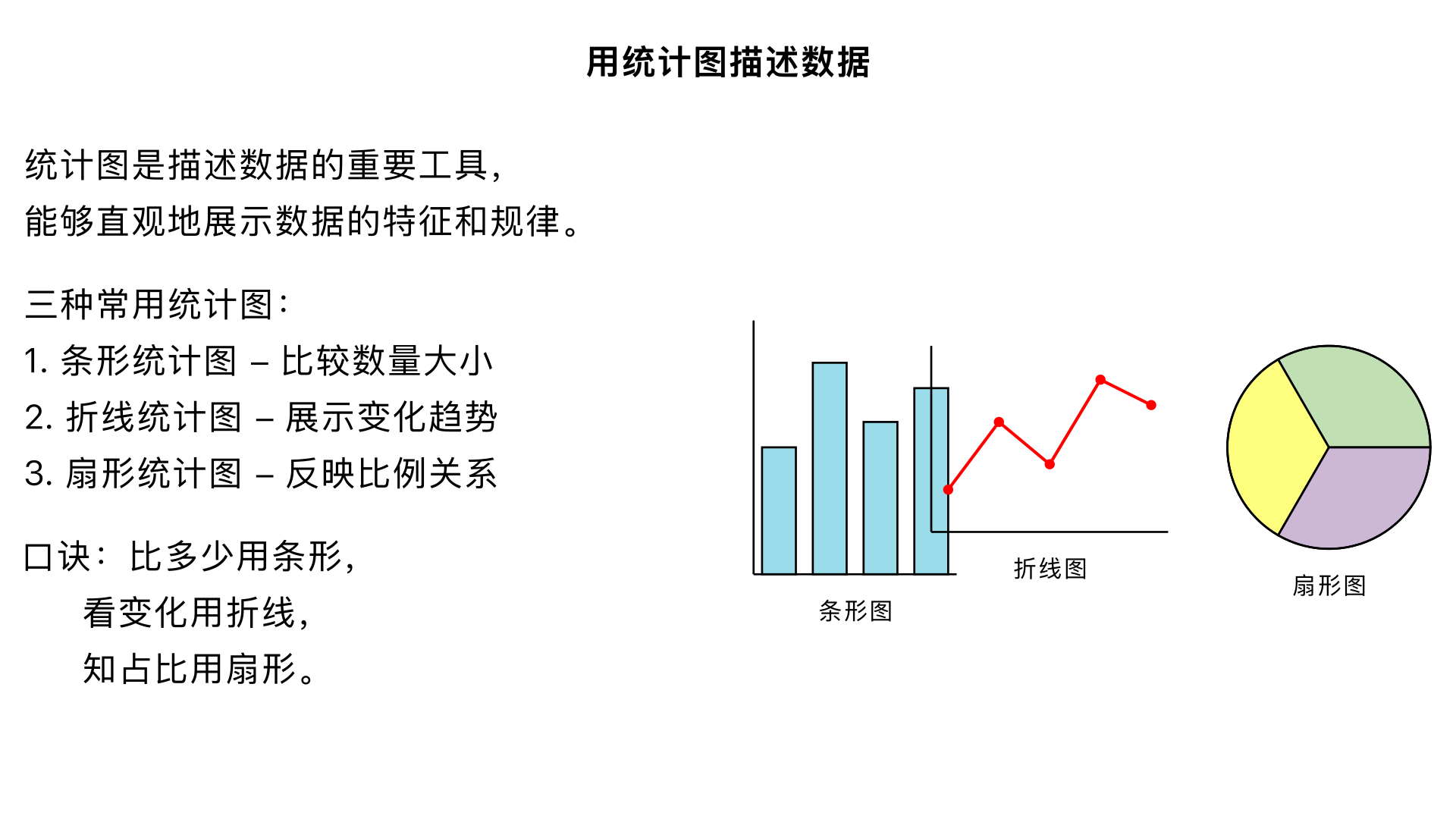
七年级数学 / 数据的收集、整理与描述 / 用统计图描述数据 一、核心目标 掌握三种常用统计图(条形统计图、折线统计图、扇形统计图)的定义、特点及适用场景; 学会根据数据类型和分析需求选择合适的统计图; 能规范绘制简单的条形统计图和折线统计图,理解扇形统计图的绘制原理; 能从统计图中准确提取有效信息,进行简单的数据分析。 二、知识点拆解(按 “定义→特点→适用场景→绘制步骤→注意事项” 层级展开) (一)条形统计图 1. 定义 用一个单位长度表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按一定的顺序排列起来的统计图。 2. 特点 直观、清晰地反映 各数据的具体数量多少; 便于比较不同类别数据之间的差异。 3. 适用场景 当需要展示 “不同类别数据的具体数值” 或 “比较各类别数据的数量大小” 时使用(如:班级同学各科成绩、不同月份的降水量、各类水果的销量等)。 4. 绘制步骤(以 “统计班级同学兴趣爱好” 为例) 步骤 具体操作 1. 定标题 明确统计图主题(如:七(1)班同学兴趣爱好统计图) 2. 画坐标轴 横轴(水平方向):标注类别(如:运动、阅读、绘画、音乐、其他); 纵轴(垂直方向):标注数量单位(如:人数),确定单位长度(如 1 格代表 2 人),确保纵轴从 0 开始 3. 画直条 根据各类别数据的数量,画出对应长度的直条(直条宽度要一致,间距要相等) 4. 标数据 在每个直条上方标注具体数值,确保清晰可读 5. 注意事项 纵轴单位长度必须统一,不能随意改变; 直条的宽度、间距要均匀,避免视觉误导; 类别名称和数值标注要完整,不遗漏。 (二)折线统计图 1. 定义 用一个单位长度表示一定的数量,根据数量的多少描出各点,然后把各点用线段顺次连接起来的统计图。 2. 特点 不仅能反映 各数据的具体数量,还能清晰展示 数据的变化趋势(上升、下降、平稳); 便于分析数据随时间或顺序的变化规律。 3. 适用场景 当需要展示 “数据随时间 / 顺序的变化情况” 时使用(如:一周内的气温变化、学生历次考试的成绩变化、一个月的销售额变化等)。 4. 绘制步骤(以 “统计一周内日均气温” 为例) 步骤 具体操作 1. 定标题 明确主题(如:周一至周日日均气温变化统计图) 2. 画坐标轴 横轴:标注时间顺序(如:周一、周二、…、周日); 纵轴:标注数量单位(如:气温 /℃),确定单位长度(如 1 格代表 1℃),从 0 开始(或根据数据范围合理设定起点,但需注明) 3. 描点 根据每天的气温数据,在对应位置描出准确的点(点的大小要适中,位置要精准) 4. 连线 用线段将各点顺次连接起来(线段要平滑,不中断) 5. 标数据 在每个点的上方或旁边标注具体数值,方便读取 5. 注意事项 横轴和纵轴的标注要清晰,单位不能遗漏; 描点要准确,连线要顺次,不能跳过或连接错误; 若数据波动较大,可适当调整纵轴的单位长度,但需保证数据的真实性。 (三)扇形统计图 1. 定义 用整个圆表示总体(单位 “1”),用圆内各个扇形的大小表示各部分数量占总体数量的百分比(即部分与总体的关系)。 2. 特点 直观反映 各部分占总体的百分比; 便于看出各部分之间的比例关系(所有扇形的百分比之和为 100%)。 3. 适用场景 当需要展示 “部分与总体的关系” 或 “各部分的比例分布” 时使用(如:班级同学各血型占比、家庭支出中各类开销占比、学校各年级人数占比等)。 4. 绘制步骤(以 “家庭月支出占比” 为例,总支出 5000 元,其中饮食 2000 元、住房 1500 元、交通 500 元、娱乐 500 元、其他 500 元) 步骤 具体操作 1. 定标题 明确主题(如:家庭月支出占比扇形统计图) 2. 算百分比 各部分占总体的百分比: 3. 算圆心角 圆的总圆心角为 360°,各扇形的圆心角 = 360°× 对应百分比: 4. 画圆和扇形 用圆规画一个圆,根据计算出的圆心角,用量角器画出各个扇形(扇形大小要与圆心角一致) 5. 标标注 在每个扇形内标注对应类别和百分比(若扇形较小,可在扇形外标注并连线); 所有扇形的百分比之和需验证是否为 100% 5. 注意事项 各部分百分比之和必须为 100%(允许因四舍五入出现微小误差); 圆心角计算要准确,量角器使用时要对齐圆心; 类别标注要清晰,避免混淆。 三、三种统计图的对比与选择技巧 统计图类型 核心优势 核心劣势 选择依据 条形统计图 清楚展示具体数量,便于比较 无法反映变化趋势和比例关系 需 “比多少”“看具体数值” 时 折线统计图 清楚展示变化趋势,兼顾具体数值 不适合比较多个类别间的比例 需 “看变化”“析规律” 时(如随时间变化) 扇形统计图 清楚展示比例关系,反映部分与总体 无法看出具体数值和变化趋势 需 “知占比”“明比例” 时 口诀记忆 “比多少用条形,看变化用折线,知占比用扇形”
▶
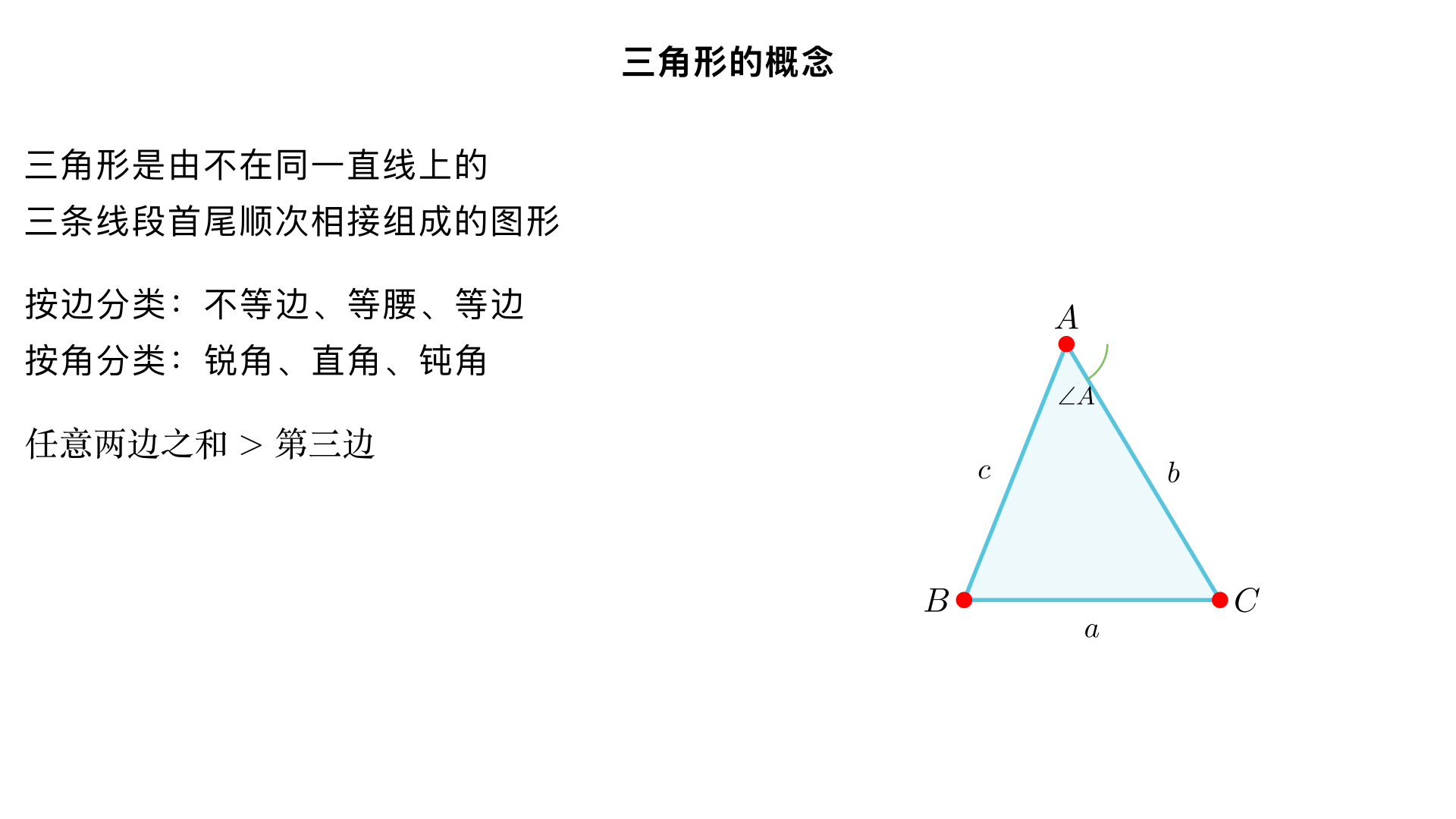
八年级数学 / 三角形 / 用三角形的概念 一、核心概念(基础必备) 1. 三角形的定义 由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。 关键词:不在同一直线、首尾顺次相接(缺一不可,若三条线段共线或未首尾相连,均不构成三角形)。 图形表示:顶点用大写字母表示(如 A、B、C),三角形记作△ABC,读作 “三角形 ABC”。 2. 三角形的构成要素 要素 定义 / 说明 表示方式 边 组成三角形的三条线段 边 AB、边 BC、边 AC(或 a、b、c,通常 a 对应 BC,b 对应 AC,c 对应 AB) 顶点 三条线段的公共端点 顶点 A、顶点 B、顶点 C 内角(简称角) 三角形相邻两边组成的角(共 3 个,且内角和为 180°,后续重点学习) ∠A、∠B、∠C(对应顶点命名) 外角 三角形的一边与另一边的延长线组成的角(共 6 个,每个内角对应 2 个外角) 如∠ACD(△ABC 中,边 BC 延长至 D,∠ACD 为∠C 的外角) 3. 三角形的表示与书写规范 记作△ABC(顶点字母无顺序要求,可写作△BAC、△ACB 等); 边的表示:可写 “边 AB” 或直接用小写字母 “c”(对应顶点 C 的对边); 角的表示:单个角用顶点字母(如∠A),若同一顶点有多个角,需用三个字母(如∠BAD,避免歧义)。 二、三角形的分类(按概念属性划分) 1. 按边的关系分类 类型 定义 关键特征 图形示意(文字描述) 不等边三角形 三条边都不相等的三角形 三边长度均不同(a≠b≠c) 三条边长度差异明显 等腰三角形 至少有两条边相等的三角形 有 “腰” 和 “底”:相等的两边为腰,第三边为底;两腰的夹角为顶角,腰与底的夹角为底角 两条边长度相同,一条不同 等边三角形 三条边都相等的三角形(特殊的等腰三角形) 三边相等(a=b=c),三个内角均为 60° 三条边长度完全相同 注意:等边三角形是等腰三角形的 “特殊情况”(满足 “至少两条边相等”),但等腰三角形不一定是等边三角形。 2. 按角的大小分类 类型 定义 关键特征 图形示意(文字描述) 锐角三角形 三个内角都是锐角(小于 90°)的三角形 三个角均<90° 三个角都比较 “尖” 直角三角形 有一个内角是直角(等于 90°)的三角形 有一个角 = 90°,另外两个角为锐角(和为 90°);直角所对的边为斜边(最长边),另外两条边为直角边 有一个角是 “直角符号” 钝角三角形 有一个内角是钝角(大于 90° 且小于 180°)的三角形 有一个角在 90°~180° 之间,另外两个角为锐角 有一个角比较 “钝” 注意:三角形中最多只有一个直角或钝角(因为内角和为 180°,若有两个直角 / 钝角,内角和会超过 180°)。 三、三角形概念的核心应用(必练题型) 题型 1:判断是否为三角形(依据定义 + 三边关系) 解题关键: 先看三条线段是否 “不在同一直线”(题目未说明时,默认不共线); 再验证 “首尾顺次相接”(几何图形题中,若线段端点相连,即满足); 补充:三角形三边关系(后续重点,但概念应用中需初步掌握)——任意两边之和大于第三边,任意两边之差小于第三边(不满足则无法构成三角形)。 例题: 下列各组线段中,能组成三角形的是( )A. 2cm、3cm、5cm B. 3cm、4cm、8cm C. 4cm、5cm、6cm D. 5cm、6cm、12cm 解析: A 选项:2+3=5,不满足 “两边之和大于第三边”,不能组成; B 选项:3+4=7<8,不满足,不能组成; C 选项:4+5=9>6,5+6=11>4,4+6=10>5,且两边之差均小于第三边,能组成; D 选项:5+6=11<12,不满足,不能组成。 答案:C 题型 2:三角形的分类判断(按边或按角) 解题关键: 按边分类:看三边长度是否相等(相等的条数); 按角分类:看最大角的度数(最大角<90°→锐角;=90°→直角;>90°→钝角)。 例题 1(按边分类): 已知△ABC 的三边长度为 AB=5cm,BC=5cm,AC=3cm,则△ABC 是( )A. 不等边三角形 B. 等腰三角形 C. 等边三角形 D. 无法确定 解析: 有两条边(AB=BC=5cm)相等,符合等腰三角形定义,且三边不都相等,不是等边三角形。答案:B 例题 2(按角分类): 已知△ABC 中,∠A=30°,∠B=60°,则△ABC 是( )A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形 解析: 内角和为 180°,则∠C=180°-30°-60°=90°,有一个直角,符合直角三角形定义。答案:B 题型 3:三角形要素的识别与表示 例题: 如图,在△ABC 中,(1)写出所有的边、顶点和内角;(2)写出∠B 的一个外角。 解析: (1)边:AB、BC、AC(或边 c、边 a、边 b);顶点:A、B、C;内角:∠A、∠B、∠C;(2)延长 BC 至点 D,则∠ACD 是∠B 的一个外角(或延长 AB 至点 E,∠CBE 是∠B 的外角)。 四、易错点提醒(避免踩坑) 混淆 “等腰三角形” 与 “等边三角形” 的关系:等边三角形是特殊的等腰三角形,不可说 “等腰三角形不是等边三角形”; 三角形外角的定义:必须是 “一边与另一边的延长线” 组成的角,不可将内角的邻补角误判为外角(如∠ABC 的邻补角是∠ABD,但需满足 D 在 AB 的延长线上); 三边关系的 “任意” 二字:需验证所有组合(如 a+b>c、a+c>b、b+c>a),不能只验证一组; 表示规范:三角形符号 “△” 不可省略,顶点字母需大写,边和角的表示要对应(如∠A 对应边 BC)。 五、知识小结(构建体系) 核心逻辑:定义(构成条件)→ 要素(边、角、顶点)→ 分类(按边 / 按角)→ 应用(判断、识别、分类); 关键联系:三角形的分类是基于 “边的长度关系” 或 “角的大小关系”,本质是对概念属性的细化; 后续衔接:本小节是三角形的基础,后续将学习三角形的内角和、外角性质、重要线段(中线、高线、角平分线)等,均需以概念为前提。 (生成一个时长在5分钟以内的视频)
▶
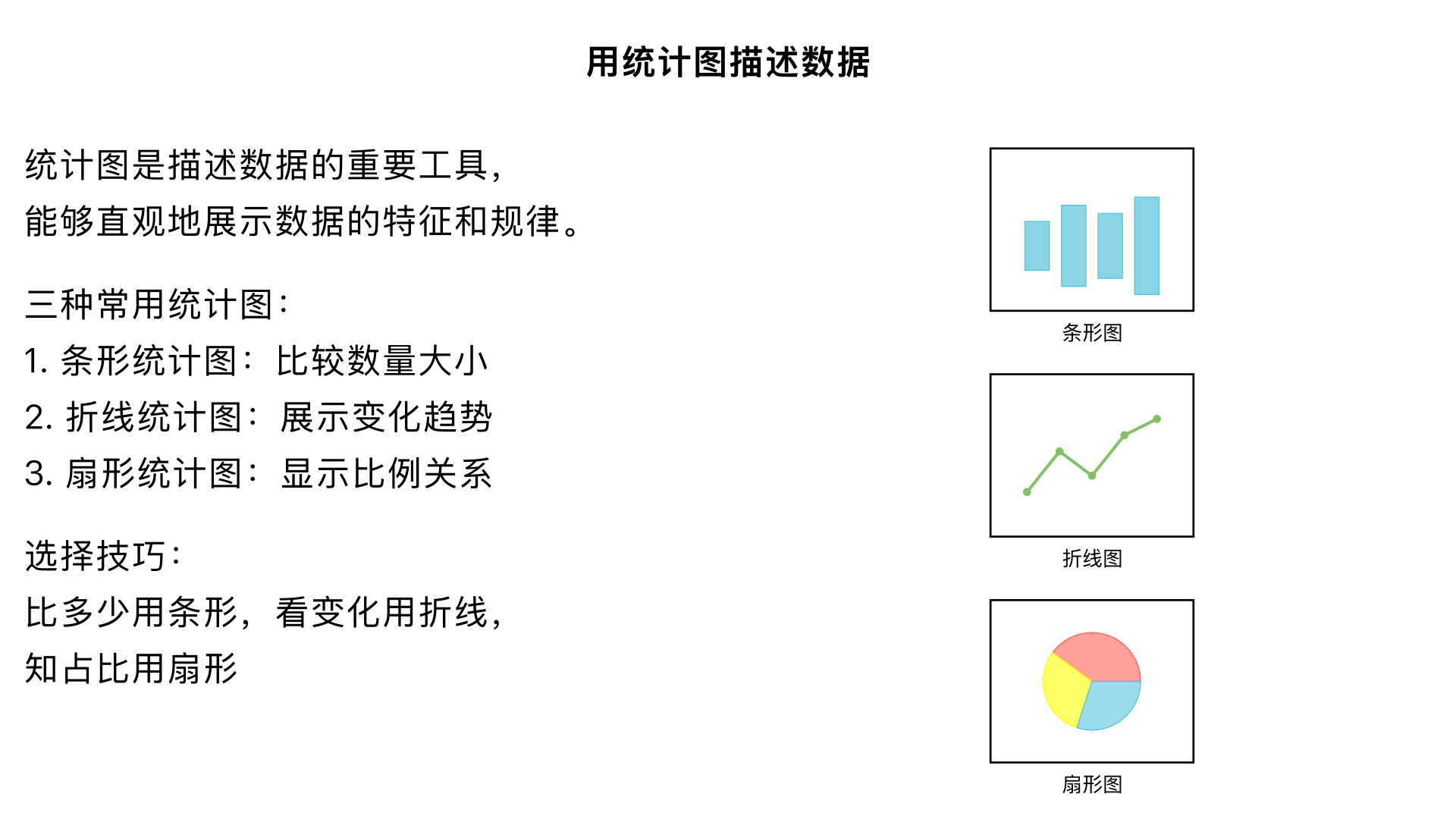
七年级数学 / 数据的收集、整理与描述 / 用统计图描述数据 一、核心目标 掌握三种常用统计图(条形统计图、折线统计图、扇形统计图)的定义、特点及适用场景; 学会根据数据类型和分析需求选择合适的统计图; 能规范绘制简单的条形统计图和折线统计图,理解扇形统计图的绘制原理; 能从统计图中准确提取有效信息,进行简单的数据分析。 二、知识点拆解(按 “定义→特点→适用场景→绘制步骤→注意事项” 层级展开) (一)条形统计图 1. 定义 用一个单位长度表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按一定的顺序排列起来的统计图。 2. 特点 直观、清晰地反映 各数据的具体数量多少; 便于比较不同类别数据之间的差异。 3. 适用场景 当需要展示 “不同类别数据的具体数值” 或 “比较各类别数据的数量大小” 时使用(如:班级同学各科成绩、不同月份的降水量、各类水果的销量等)。 4. 绘制步骤(以 “统计班级同学兴趣爱好” 为例) 步骤 具体操作 1. 定标题 明确统计图主题(如:七(1)班同学兴趣爱好统计图) 2. 画坐标轴 横轴(水平方向):标注类别(如:运动、阅读、绘画、音乐、其他); 纵轴(垂直方向):标注数量单位(如:人数),确定单位长度(如 1 格代表 2 人),确保纵轴从 0 开始 3. 画直条 根据各类别数据的数量,画出对应长度的直条(直条宽度要一致,间距要相等) 4. 标数据 在每个直条上方标注具体数值,确保清晰可读 5. 注意事项 纵轴单位长度必须统一,不能随意改变; 直条的宽度、间距要均匀,避免视觉误导; 类别名称和数值标注要完整,不遗漏。 (二)折线统计图 1. 定义 用一个单位长度表示一定的数量,根据数量的多少描出各点,然后把各点用线段顺次连接起来的统计图。 2. 特点 不仅能反映 各数据的具体数量,还能清晰展示 数据的变化趋势(上升、下降、平稳); 便于分析数据随时间或顺序的变化规律。 3. 适用场景 当需要展示 “数据随时间 / 顺序的变化情况” 时使用(如:一周内的气温变化、学生历次考试的成绩变化、一个月的销售额变化等)。 4. 绘制步骤(以 “统计一周内日均气温” 为例) 步骤 具体操作 1. 定标题 明确主题(如:周一至周日日均气温变化统计图) 2. 画坐标轴 横轴:标注时间顺序(如:周一、周二、…、周日); 纵轴:标注数量单位(如:气温 /℃),确定单位长度(如 1 格代表 1℃),从 0 开始(或根据数据范围合理设定起点,但需注明) 3. 描点 根据每天的气温数据,在对应位置描出准确的点(点的大小要适中,位置要精准) 4. 连线 用线段将各点顺次连接起来(线段要平滑,不中断) 5. 标数据 在每个点的上方或旁边标注具体数值,方便读取 5. 注意事项 横轴和纵轴的标注要清晰,单位不能遗漏; 描点要准确,连线要顺次,不能跳过或连接错误; 若数据波动较大,可适当调整纵轴的单位长度,但需保证数据的真实性。 (三)扇形统计图 1. 定义 用整个圆表示总体(单位 “1”),用圆内各个扇形的大小表示各部分数量占总体数量的百分比(即部分与总体的关系)。 2. 特点 直观反映 各部分占总体的百分比; 便于看出各部分之间的比例关系(所有扇形的百分比之和为 100%)。 3. 适用场景 当需要展示 “部分与总体的关系” 或 “各部分的比例分布” 时使用(如:班级同学各血型占比、家庭支出中各类开销占比、学校各年级人数占比等)。 4. 绘制步骤(以 “家庭月支出占比” 为例,总支出 5000 元,其中饮食 2000 元、住房 1500 元、交通 500 元、娱乐 500 元、其他 500 元) 步骤 具体操作 1. 定标题 明确主题(如:家庭月支出占比扇形统计图) 2. 算百分比 各部分占总体的百分比: 饮食:2000÷5000=40%;住房:1500÷5000=30%; 交通:500÷5000=10%;娱乐:500÷5000=10%;其他:500÷5000=10% 3. 算圆心角 圆的总圆心角为 360°,各扇形的圆心角 = 360°× 对应百分比: 饮食:360°×40%=144°;住房:360°×30%=108°; 交通:360°×10%=36°;娱乐:360°×10%=36°;其他:360°×10%=36° 4. 画圆和扇形 用圆规画一个圆,根据计算出的圆心角,用量角器画出各个扇形(扇形大小要与圆心角一致) 5. 标标注 在每个扇形内标注对应类别和百分比(若扇形较小,可在扇形外标注并连线); 所有扇形的百分比之和需验证是否为 100% 5. 注意事项 各部分百分比之和必须为 100%(允许因四舍五入出现微小误差); 圆心角计算要准确,量角器使用时要对齐圆心; 类别标注要清晰,避免混淆。 三、三种统计图的对比与选择技巧 统计图类型 核心优势 核心劣势 选择依据 条形统计图 清楚展示具体数量,便于比较 无法反映变化趋势和比例关系 需 “比多少”“看具体数值” 时 折线统计图 清楚展示变化趋势,兼顾具体数值 不适合比较多个类别间的比例 需 “看变化”“析规律” 时(如随时间变化) 扇形统计图 清楚展示比例关系,反映部分与总体 无法看出具体数值和变化趋势 需 “知占比”“明比例” 时 口诀记忆 “比多少用条形,看变化用折线,知占比用扇形” 四、典型例题(基础 + 应用) 例题 1:基础选择 下列情况中,适合用扇形统计图的是( )A. 统计某班同学的身高数据B. 统计某市 2023 年每月的用电量C. 统计某品牌手机各型号的销量占比D. 统计小明本学期 5 次数学考试的成绩 答案:C解析: A 选项需展示具体数值,用条形统计图;B 选项需展示随时间的变化,用折线统计图;C 选项需展示部分与总体的占比,用扇形统计图;D 选项需展示成绩变化,用折线统计图。 例题 2:应用绘制与分析 某校对七年级 500 名学生的课外活动情况进行调查,结果如下:运动 150 人,阅读 200 人,兴趣小组 100 人,其他 50 人。(1)请计算各部分占总体的百分比;(2)选择合适的统计图描述该数据,并说明理由;(3)从统计图中你能获得什么信息? 解答:(1)百分比计算:运动:150÷500=30%;阅读:200÷500=40%;兴趣小组:100÷500=20%;其他:50÷500=10%。 (2)选择扇形统计图(理由:需展示各课外活动类型占总人数的比例关系);若需比较各类型的具体人数,也可选择条形统计图。 (3)信息提取(示例):① 阅读是七年级学生最主要的课外活动,占比 40%;② 运动和兴趣小组的人数占比分别为 30% 和 20%;③ 参与 “其他” 课外活动的学生占比最少,仅 10%。 五、易错点总结 条形统计图纵轴未从 0 开始,导致直条长度与实际数量比例不符; 折线统计图连线错误(未顺次连接)或漏标数据点; 扇形统计图百分比之和不为 100%(计算错误)或圆心角绘制不准确; 选择统计图时混淆适用场景(如用折线统计图展示比例关系)。 六、练习巩固 统计你所在班级同学的数学成绩(按 “优秀 / 良好 / 及格 / 不及格” 分类),绘制条形统计图,并计算各等级的占比; 记录一周内每天的睡眠时间,绘制折线统计图,分析自己的睡眠变化趋势; 调查家庭月收入的分配情况(如:生活费、教育费、储蓄、娱乐等),绘制扇形统计图,并说明各部分占比是否合理。
▶
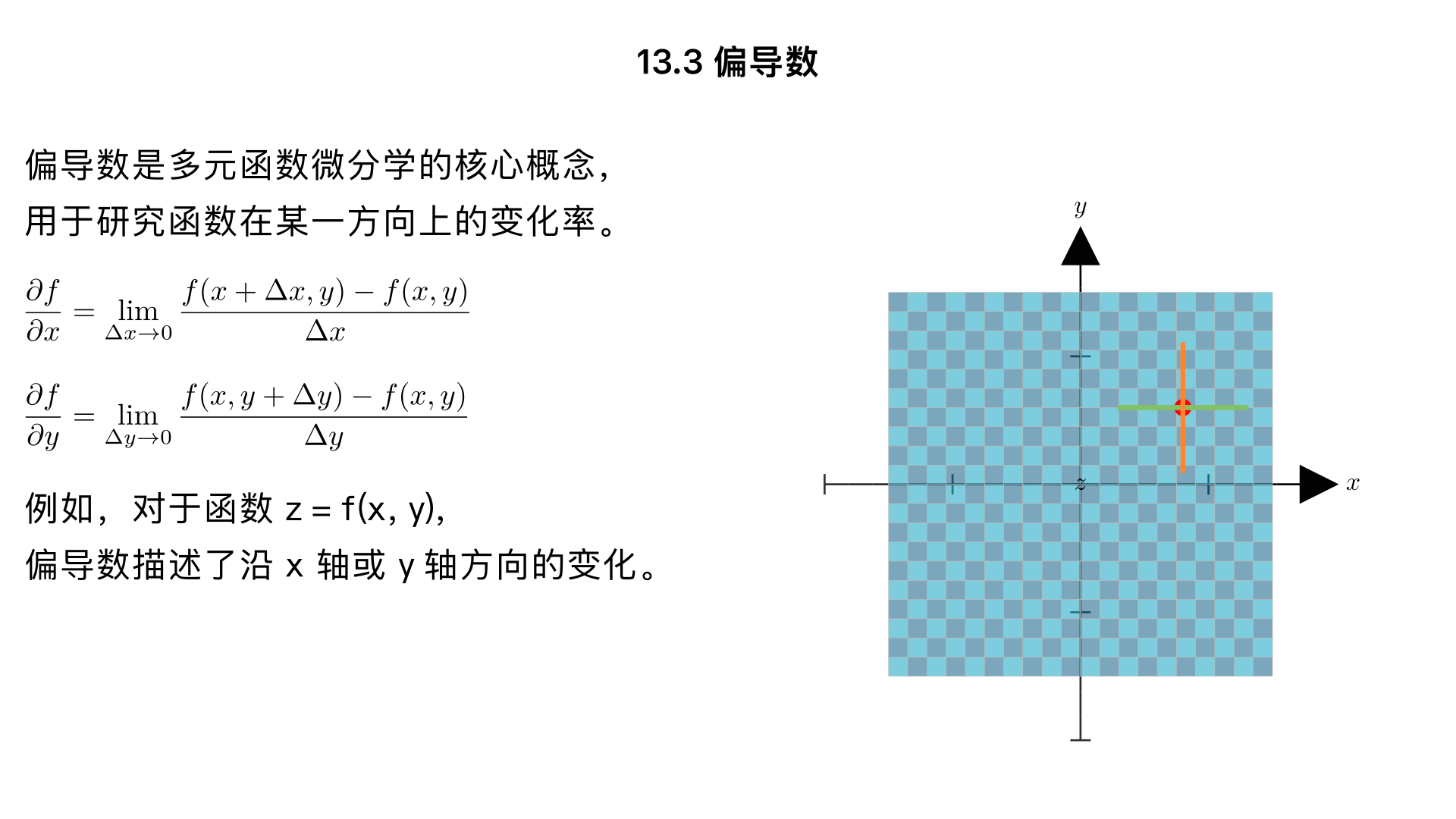
13.3 偏导数
▶
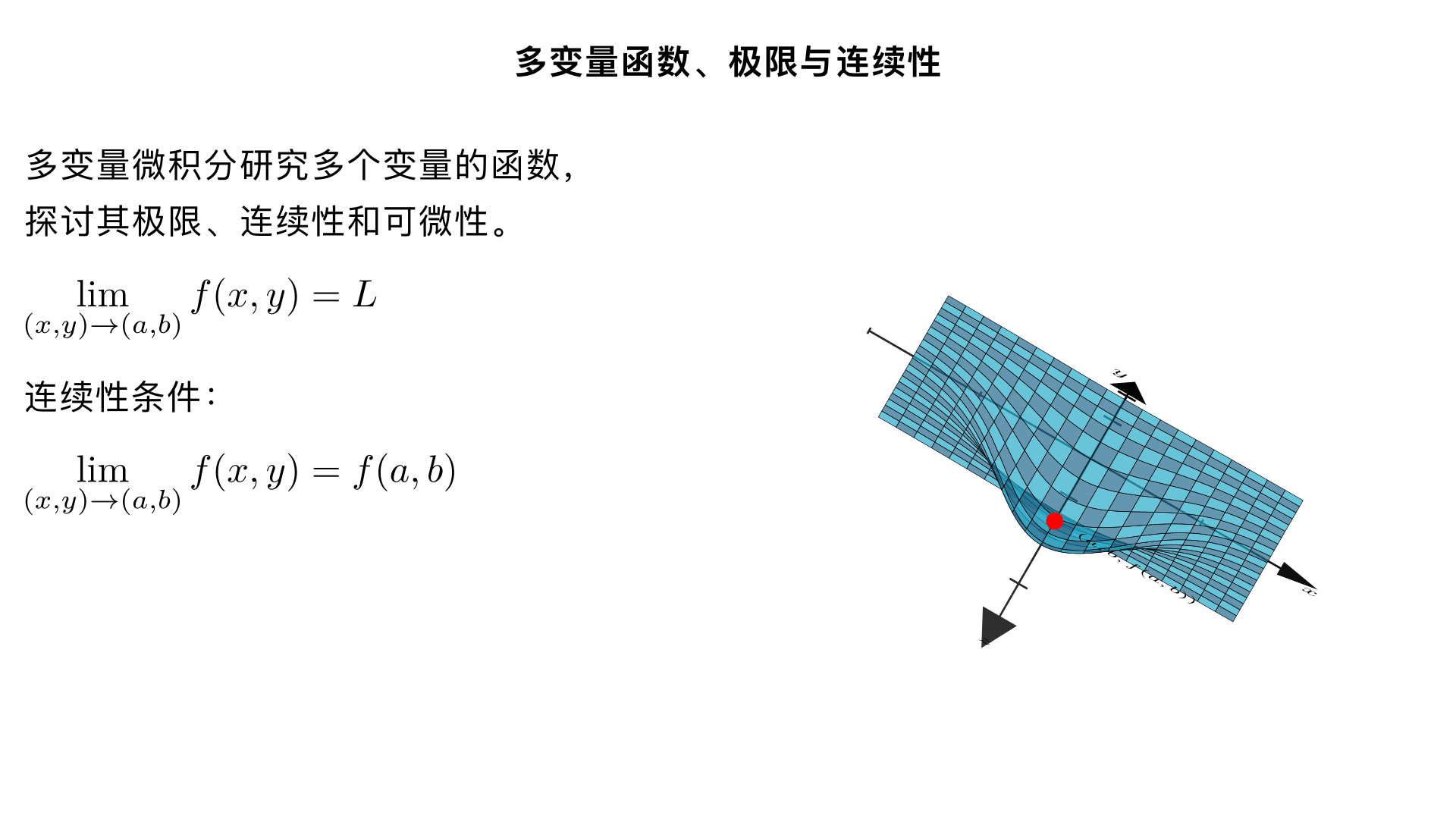
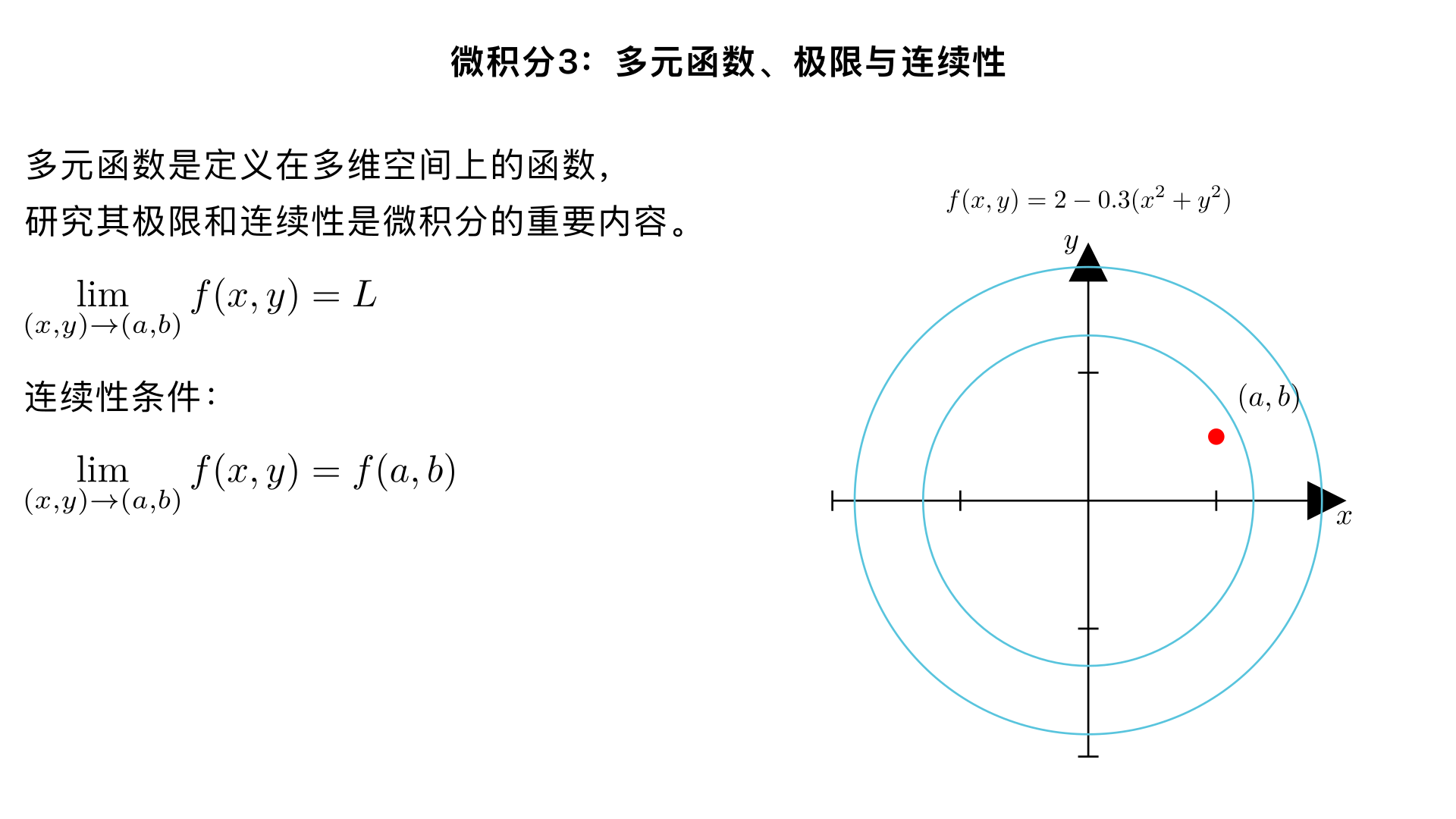
Calculus 3: Multivariable Functions, Limits, and Continuity
▶
Calculus 3: Multivariable Functions, Limits, and Continuity

▶
Calculus 3: Multivariable Functions, Limits, and Continuity

▶
Calculus 3: Multivariable Functions, Limits, and Continuity

▶