T
Teach Me AnythingTMA
Video History
Page 8 / 43
▶
蹇解二卦的辩证智慧 一、蹇解二卦的对照分析 维度 蹇卦(䷦) 解卦(䷧) 卦象 山上有水,险阻在前 雷雨作,生机勃发 时境 艰难困顿之时 危难解除之后 卦德 见险而能止 险以动,动而免乎险 方向 利西南,不利东北 利西南,往得众 关键 利见大人 其来复吉 大象 反身修德 赦过宥罪 爻辞核心 王臣蹇蹇,匪躬之故 负且乘,致寇至 二、金景芳易学的特色体现 1. 紧扣《彖传》《象传》 蹇卦突出“见险而能止”和“反身修德” 解卦突出“险以动”和“赦过宥罪” 2. 历史与易理结合 蹇卦引用文王、诸葛亮等事例 解卦引用周公、汉高祖等事例 3. 现实关怀 蹇卦对个人面对逆境的指导 解卦对组织危机善后的启示 三、蹇解二卦的现代应用 1. 个人层面 面对困难(蹇):反身修德,寻求贵人,选择方向 解决困难后(解):不炫耀,肃清隐患,宽恕他人 2. 组织层面 企业危机时(蹇):暂停业务,反省战略,寻找外部帮助 危机过后(解):恢复秩序,处理遗留问题,防止危机复发 3. 国家层面 国家困难时期(蹇):休养生息,争取外援,坚持正道 困难解除后(解):大赦天下,安抚民心,巩固政权 四、学习要点 1. 核心背诵 蹇卦彖传:“蹇,难也,险在前也…” 解卦彖传:“解,险以动,动而免乎险…” 大象传:“君子以反身修德”“君子以赦过宥罪” 2. 重点掌握 蹇卦“利西南”“见大人”的策略意义 解卦“负且乘,致寇至”的警示意义 二卦的对应关系:止险与动险 3. 思考应用 你当前面临的“蹇”境是什么?如何“反身修德”? 你过去解决的困难中,是否有“负且乘”的错误? 如何理解“赦过宥罪”在现代社会的应用? 4. 延伸阅读 《孟子》“生于忧患,死于安乐”与蹇卦互参 《尚书》“康诰”“酒诰”与解卦“赦过宥罪”互证 现代著作:塔勒布《反脆弱》——如何从困难中受益 通过这两课的深入学习,您将掌握《周易》中关于面对困难和解除困难的核心智慧。金景芳先生的解读,展现了儒家在逆境中修德待时、在顺境中谨慎善后的完整人生哲学。
▶
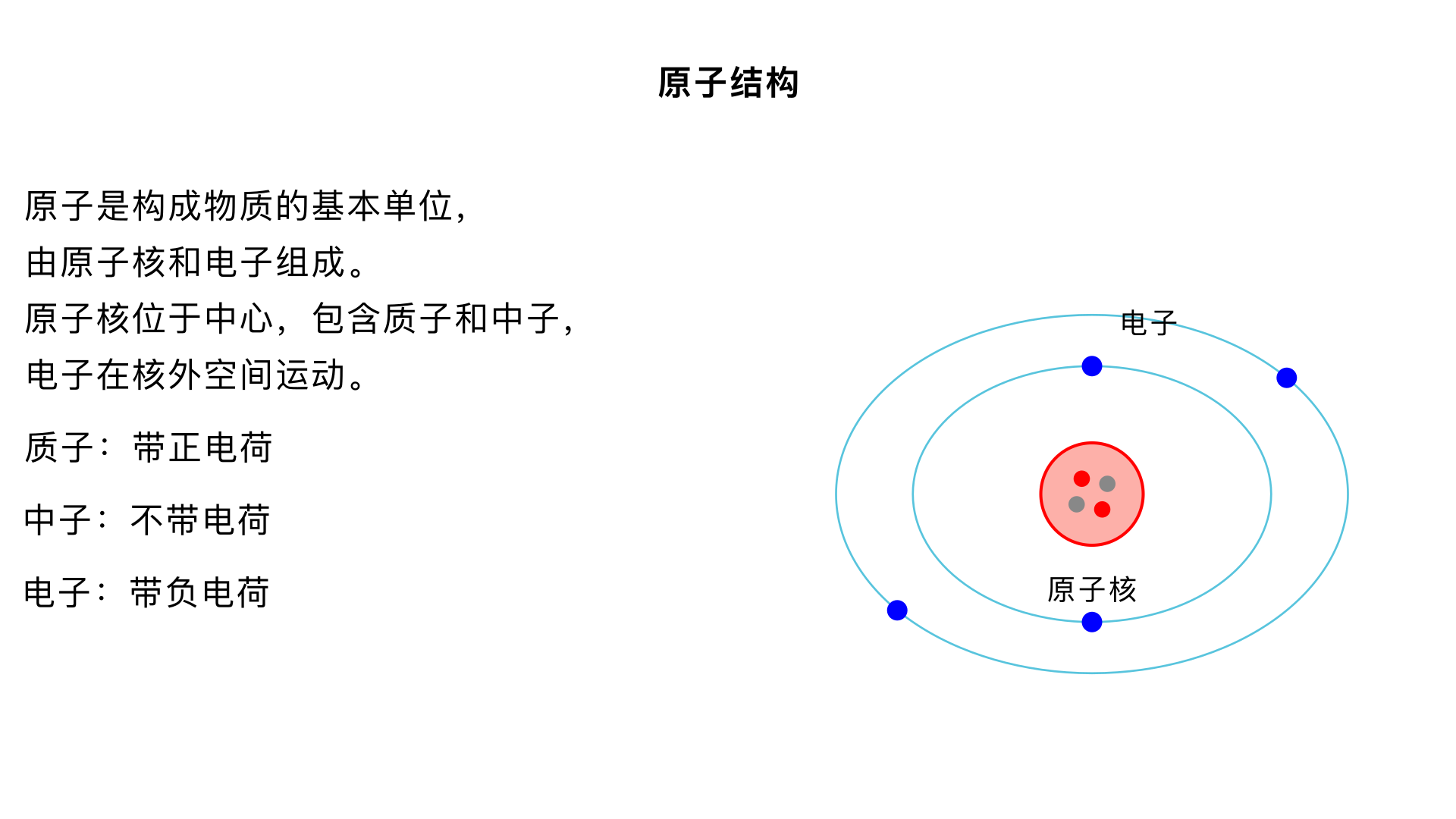
帮我用视频讲解原子结构
▶
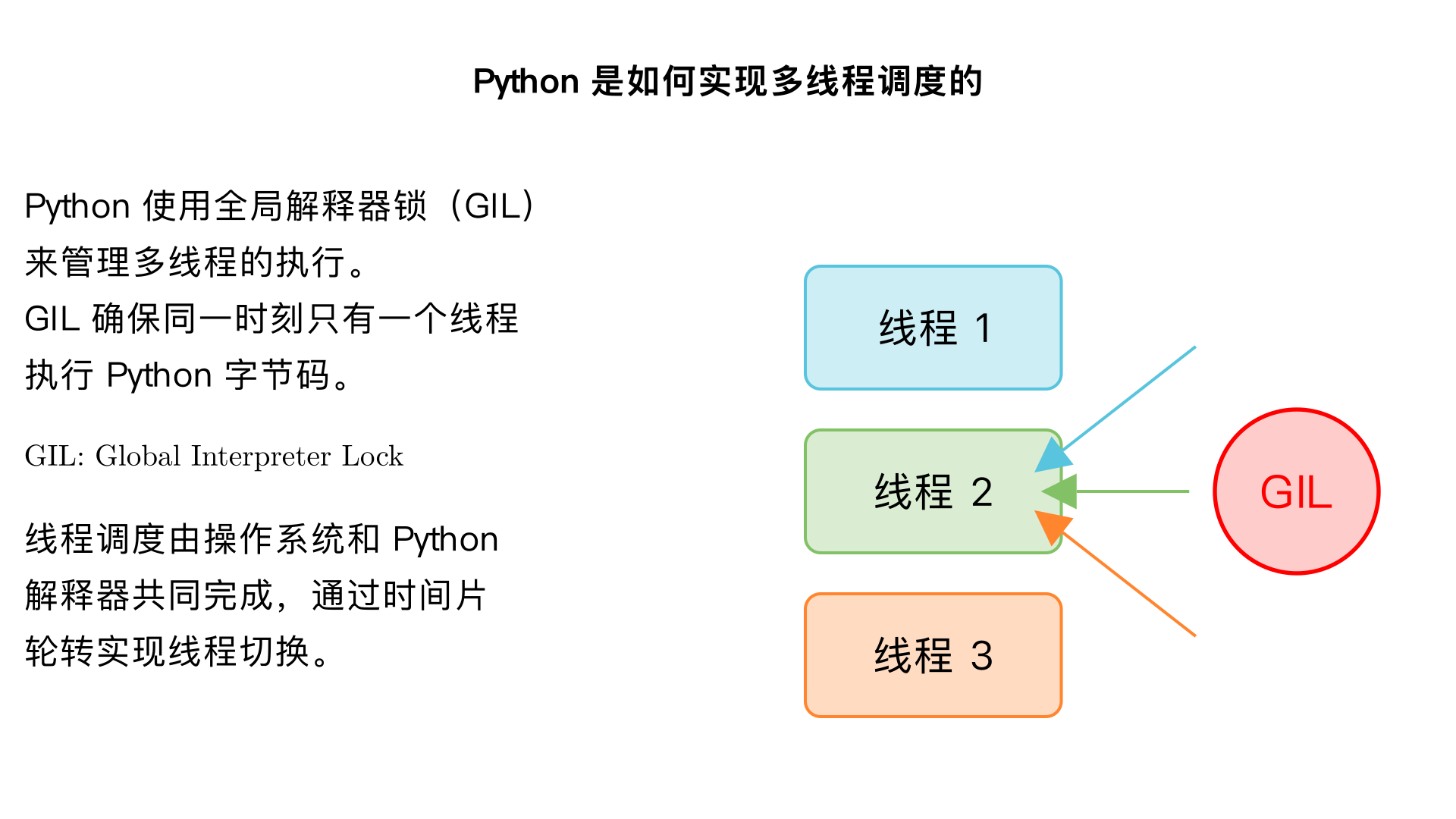
Python 是如何实现多线程调度的
▶
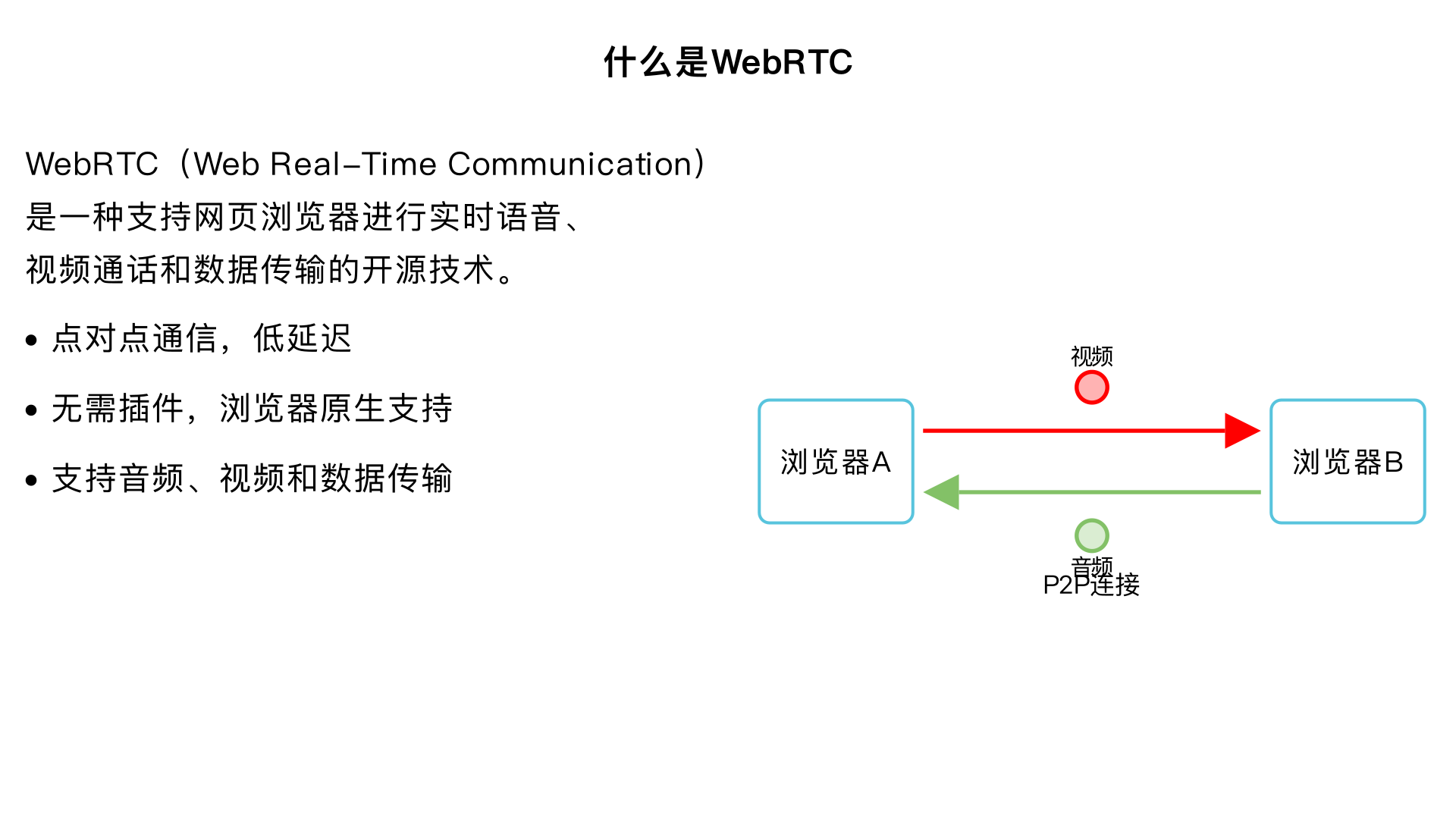
什么是webrtc

▶
CPU是如何保存用户态的上下文的
▶
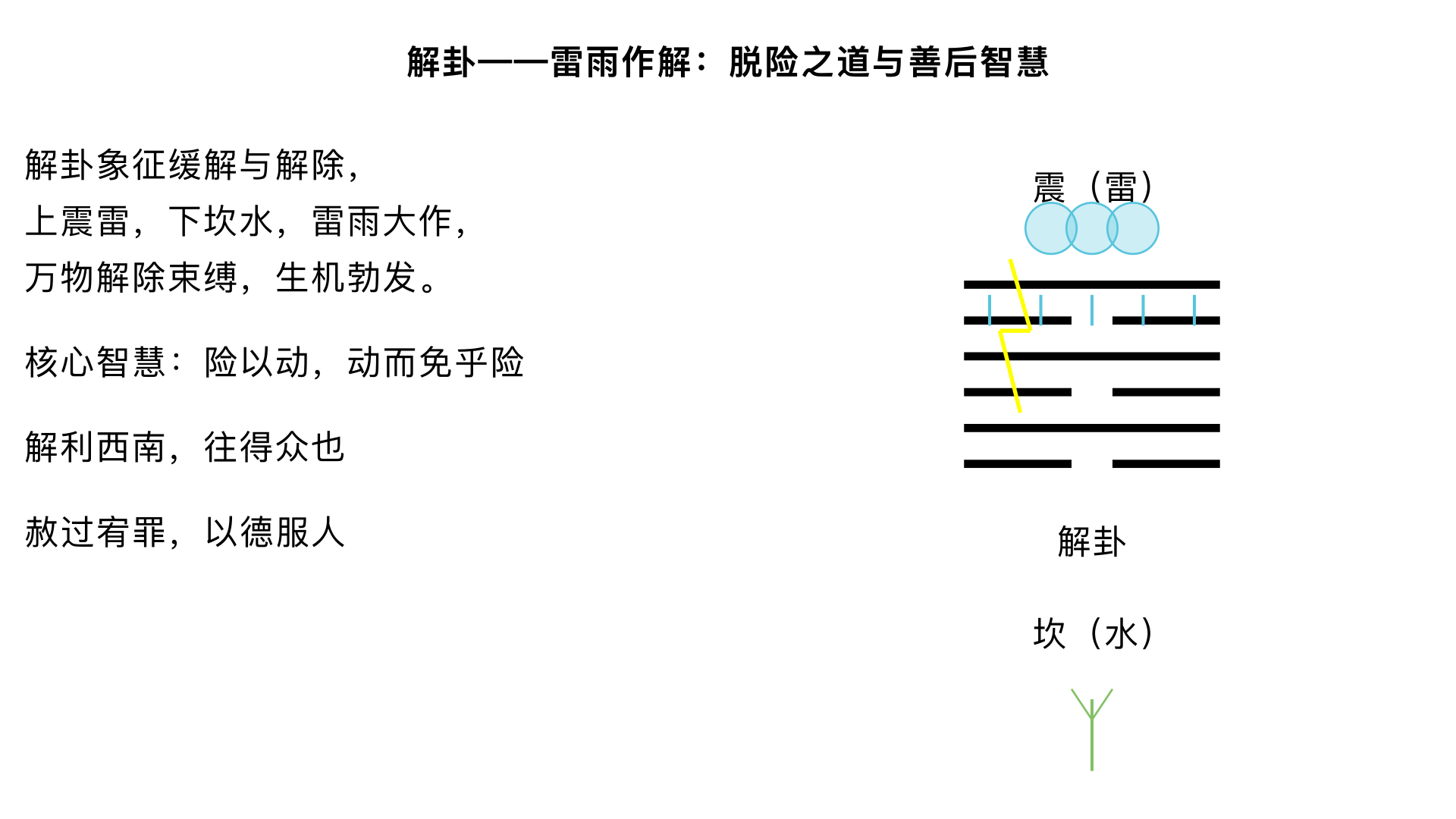
主题:解卦——雷雨作解:脱险之道与善后智慧 一、卦序逻辑:从艰难到缓解 1. 《序卦传》的必然转化 “蹇者,难也。物不可以终难,故受之以解。解者,缓也。” 蹇卦(水山蹇)象征艰难险阻 → 但事物不会永远处于艰难中 → 解卦(雷水解)象征缓解、解除 金景芳指出:这体现了《周易》“穷则变,变则通”的辩证思想 2. 蹇卦与解卦的综卦关系 蹇卦(䷦):上坎下艮,山上有水,险阻在前 解卦(䷧):上震下坎,雷雨作,百果草木皆甲坼(生机勃发) 二卦互为综卦(将蹇卦上下颠倒即得解卦),表明险难与解除是同一过程的不同阶段 二、解卦(雷水解)卦象的解放之象 1. “雷雨作”的生机勃发 基本卦象:上震雷,下坎水 → 雷雨大作,滋润万物 自然象征: 冬季(坎为水,为冬)过后,春雷(震为雷,为春)震动,雨水降临,冰消雪融 万物解除束缚,破壳而出(“百果草木皆甲坼”) 金景芳引申:此象喻示政治严苛(坎险)之后,仁政施行(震动),万民获得新生 2. 卦德分析与行动原则 下坎为险,上震为动 → 动而出险 《彖传》:“解,险以动,动而免乎险,解。” 核心智慧:在险境中积极行动,通过行动脱离险境 3. 爻位结构中的隐患 六三阴柔失正,上六无应 → 提示解难后可能产生新的问题 九二、九四阳刚有力,为解难主力 金景芳提醒:解卦不是一劳永逸,需防“致寇至” 三、彖传精解:解困之道 “解,险以动,动而免乎险,解。 解利西南,往得众也。 其来复吉,乃得中也。 有攸往夙吉,往有功也。 天地解而雷雨作,雷雨作而百果草木皆甲坼。 解之时大矣哉!” 1. “险以动,动而免乎险”的行动哲学 辩证关系:险境中行动(险以动),行动才能脱险(动而免乎险) 历史例证:刘邦被围荥阳,用陈平计突围(动),终免于险 反面教材:宋襄公“不鼓不成列”,坐失战机,未“动而免乎险” 2. “解利西南,往得众也”的民心指向 西南象征:坤方,平地,众庶(坤为众) “往得众”:前往西南可得民众支持 与蹇卦呼应:蹇卦“利西南”为避险,解卦“利西南”为得众 政治智慧:解难后需争取民心,如武王克商后“释箕子囚,封比干墓” 3. “其来复吉,乃得中也”的回归原则 “来复”:回归常态,恢复秩序 “得中”:符合中道(指九二居中) 政策启示:动乱平息后,应休养生息,恢复常规 历史例证:汉初萧何“与民休息”,是“其来复吉” 4. “有攸往夙吉,往有功也”的时效原则 “夙吉”:及早行动则吉(夙,早也) “往有功”:前往可建功业 战术要求:解决遗留问题要迅速,如周公东征速平管蔡之乱 5. “天地解而雷雨作…”的自然意象升华 将人事解脱与天地生化相联系 寓意:政治解困如雷雨滋润万物,带来生机 金景芳阐发:解卦蕴含“革命解放”的正当性,如汤武革命“顺乎天而应乎人” 6. “解之时大矣哉!”的赞叹 解卦的时义太重大了! 强调:把握解难时机的重要性,早则不及,迟则生变 四、大象传:“赦过宥罪”的宽恕精神 “雷雨作,解。君子以赦过宥罪。” 1. “赦过宥罪”的政治智慧 赦过:赦免无心过失 宥罪:宽恕有意罪过(但非免除惩罚,是减刑) 与《尚书》互证:“眚灾肆赦,怙终贼刑”(过失犯罪可赦,惯犯严惩) 2. 历史应用 汉文帝废肉刑:体现“宥罪”精神 唐太宗纵囚:风险之举,但收服人心 现代意义:战后和解、转型正义中的宽恕政策 3. 金景芳提醒:“赦过宥罪”不是无原则宽大,而是“解”后争取人心的策略 五、爻辞精析:解难的六个要点 解卦六爻侧重解难之后如何巩固成果、防止反复,是一套“善后指南”。 1. 初六:无咎。 简短爻辞,深意存焉:初六阴柔居解始,与九四正应 “无咎”条件:解难之初,低调顺从(上应九四),不争功,故无咎 象征:普通民众在解放后安分守己,可得无咎 历史情景:商民在周克商后,服从新朝,得保平安 2. 九二:田获三狐,得黄矢,贞吉。 “田获三狐”:田猎获得多只狐狸(狐象征小人、隐患) “得黄矢”:得到黄色箭矢(黄为中色,矢为直,象征中直之道) 爻象:九二阳刚居中,为解难主力 含义: 解难后需肃清余孽(三狐) 方法要中正(黄矢) 历史例证:周公诛管叔、放蔡叔、囚霍叔(三狐),但存中道(不滥杀) 3. 六三:负且乘,致寇至,贞吝。 全卦核心警示,源自孔子在《系辞传》中的重点阐发 生动画面: “负且乘”:背着财物坐在车上(小人得志,炫耀富贵) “致寇至”:招致强盗来抢 爻象:六三阴柔失正,居下卦之上,象征才德不配位的小人 孔子阐发(《系辞上》第八章): “作《易》者其知盗乎?…小人而乘君子之器,盗思夺之矣。” 揭示:德不配位,必招灾祸 现实意义:企业危机后,管理者若炫耀成功,可能引发新的危机 4. 九四:解而拇,朋至斯孚。 “解而拇”:解开你大脚趾的束缚(拇,足大趾,指初六) “朋至斯孚”:朋友到来,以诚信相待 爻象:九四阳居阴位,刚柔相济,下应初六 策略:解脱基层束缚(解而拇),则民众(朋)诚心归附(斯孚) 政策对应:汉高祖“约法三章”,解秦苛法,得关中民心 5. 六五:君子维有解,吉。有孚于小人。 “君子维有解”:君子被捆绑又得解脱(维,系也) “吉”:吉祥 “有孚于小人”:以诚信感化小人 爻象:六五柔中居尊,下应九二,处震卦中位 领袖之道: 自身曾受困(维),终得解 掌权后不报复,以诚信待小人(包括曾经的敌人) 历史典范:齐桓公不记管仲射钩之仇,任用为相,终成霸业 6. 上六:公用射隼于高墉之上,获之,无不利。 生动比喻: “公用射隼”:王公射杀凶鸟(隼,猛禽,象征残存的恶势力) “于高墉之上”:在高墙上(墉,城墙,象征险要位置) 爻象:上六处解之终,仍有隐患(隼)居高墉,需彻底清除 “获之,无不利”:擒获它,无所不利 历史例证:汉武帝彻底解决诸侯王问题(推恩令),巩固统一 金景芳总结:解卦以“射隼”作结,强调解难的彻底性 六、解卦的解难智慧总论 1. 行动原则:“险以动,动而免乎险” 积极行动,脱出险境 2. 政治方向:“利西南,往得众” 解难后争取民心,稳定大局 3. 善后要务: 肃清余孽(田获三狐) 防止炫耀(负且乘) 解脱民困(解而拇) 感化小人(有孚于小人) 清除顽敌(射隼高墉) 4. 宽恕精神:“赦过宥罪” 但宽恕有度,不是无限赦免 5. 金景芳总结:解卦是儒家“拨乱反正”思想的体现,强调解难要彻底,善后要谨慎,治国要以德服人。
▶
解卦——雷雨作解:脱险之道与善后智慧 一、卦序逻辑:从艰难到缓解 1. 《序卦传》的必然转化 “蹇者,难也。物不可以终难,故受之以解。解者,缓也。” 蹇卦(水山蹇)象征艰难险阻 → 但事物不会永远处于艰难中 → 解卦(雷水解)象征缓解、解除 金景芳指出:这体现了《周易》“穷则变,变则通”的辩证思想 2. 蹇卦与解卦的综卦关系 蹇卦(䷦):上坎下艮,山上有水,险阻在前 解卦(䷧):上震下坎,雷雨作,百果草木皆甲坼(生机勃发) 二卦互为综卦(将蹇卦上下颠倒即得解卦),表明险难与解除是同一过程的不同阶段 二、解卦(雷水解)卦象的解放之象 1. “雷雨作”的生机勃发 基本卦象:上震雷,下坎水 → 雷雨大作,滋润万物 自然象征: 冬季(坎为水,为冬)过后,春雷(震为雷,为春)震动,雨水降临,冰消雪融 万物解除束缚,破壳而出(“百果草木皆甲坼”) 金景芳引申:此象喻示政治严苛(坎险)之后,仁政施行(震动),万民获得新生 2. 卦德分析与行动原则 下坎为险,上震为动 → 动而出险 《彖传》:“解,险以动,动而免乎险,解。” 核心智慧:在险境中积极行动,通过行动脱离险境 3. 爻位结构中的隐患 六三阴柔失正,上六无应 → 提示解难后可能产生新的问题 九二、九四阳刚有力,为解难主力 金景芳提醒:解卦不是一劳永逸,需防“致寇至” 三、彖传精解:解困之道 “解,险以动,动而免乎险,解。 解利西南,往得众也。 其来复吉,乃得中也。 有攸往夙吉,往有功也。 天地解而雷雨作,雷雨作而百果草木皆甲坼。 解之时大矣哉!” 1. “险以动,动而免乎险”的行动哲学 辩证关系:险境中行动(险以动),行动才能脱险(动而免乎险) 历史例证:刘邦被围荥阳,用陈平计突围(动),终免于险 反面教材:宋襄公“不鼓不成列”,坐失战机,未“动而免乎险” 2. “解利西南,往得众也”的民心指向 西南象征:坤方,平地,众庶(坤为众) “往得众”:前往西南可得民众支持 与蹇卦呼应:蹇卦“利西南”为避险,解卦“利西南”为得众 政治智慧:解难后需争取民心,如武王克商后“释箕子囚,封比干墓” 3. “其来复吉,乃得中也”的回归原则 “来复”:回归常态,恢复秩序 “得中”:符合中道(指九二居中) 政策启示:动乱平息后,应休养生息,恢复常规 历史例证:汉初萧何“与民休息”,是“其来复吉” 4. “有攸往夙吉,往有功也”的时效原则 “夙吉”:及早行动则吉(夙,早也) “往有功”:前往可建功业 战术要求:解决遗留问题要迅速,如周公东征速平管蔡之乱 5. “天地解而雷雨作…”的自然意象升华 将人事解脱与天地生化相联系 寓意:政治解困如雷雨滋润万物,带来生机 金景芳阐发:解卦蕴含“革命解放”的正当性,如汤武革命“顺乎天而应乎人” 6. “解之时大矣哉!”的赞叹 解卦的时义太重大了! 强调:把握解难时机的重要性,早则不及,迟则生变 四、大象传:“赦过宥罪”的宽恕精神 “雷雨作,解。君子以赦过宥罪。” 1. “赦过宥罪”的政治智慧 赦过:赦免无心过失 宥罪:宽恕有意罪过(但非免除惩罚,是减刑) 与《尚书》互证:“眚灾肆赦,怙终贼刑”(过失犯罪可赦,惯犯严惩) 2. 历史应用 汉文帝废肉刑:体现“宥罪”精神 唐太宗纵囚:风险之举,但收服人心 现代意义:战后和解、转型正义中的宽恕政策 3. 金景芳提醒:“赦过宥罪”不是无原则宽大,而是“解”后争取人心的策略 五、爻辞精析:解难的六个要点 解卦六爻侧重解难之后如何巩固成果、防止反复,是一套“善后指南”。 1. 初六:无咎。 简短爻辞,深意存焉:初六阴柔居解始,与九四正应 “无咎”条件:解难之初,低调顺从(上应九四),不争功,故无咎 象征:普通民众在解放后安分守己,可得无咎 历史情景:商民在周克商后,服从新朝,得保平安 2. 九二:田获三狐,得黄矢,贞吉。 “田获三狐”:田猎获得多只狐狸(狐象征小人、隐患) “得黄矢”:得到黄色箭矢(黄为中色,矢为直,象征中直之道) 爻象:九二阳刚居中,为解难主力 含义: 解难后需肃清余孽(三狐) 方法要中正(黄矢) 历史例证:周公诛管叔、放蔡叔、囚霍叔(三狐),但存中道(不滥杀) 3. 六三:负且乘,致寇至,贞吝。 全卦核心警示,源自孔子在《系辞传》中的重点阐发 生动画面: “负且乘”:背着财物坐在车上(小人得志,炫耀富贵) “致寇至”:招致强盗来抢 爻象:六三阴柔失正,居下卦之上,象征才德不配位的小人 孔子阐发(《系辞上》第八章): “作《易》者其知盗乎?…小人而乘君子之器,盗思夺之矣。” 揭示:德不配位,必招灾祸 现实意义:企业危机后,管理者若炫耀成功,可能引发新的危机 4. 九四:解而拇,朋至斯孚。 “解而拇”:解开你大脚趾的束缚(拇,足大趾,指初六) “朋至斯孚”:朋友到来,以诚信相待 爻象:九四阳居阴位,刚柔相济,下应初六 策略:解脱基层束缚(解而拇),则民众(朋)诚心归附(斯孚) 政策对应:汉高祖“约法三章”,解秦苛法,得关中民心 5. 六五:君子维有解,吉。有孚于小人。 “君子维有解”:君子被捆绑又得解脱(维,系也) “吉”:吉祥 “有孚于小人”:以诚信感化小人 爻象:六五柔中居尊,下应九二,处震卦中位 领袖之道: 自身曾受困(维),终得解 掌权后不报复,以诚信待小人(包括曾经的敌人) 历史典范:齐桓公不记管仲射钩之仇,任用为相,终成霸业 6. 上六:公用射隼于高墉之上,获之,无不利。 生动比喻: “公用射隼”:王公射杀凶鸟(隼,猛禽,象征残存的恶势力) “于高墉之上”:在高墙上(墉,城墙,象征险要位置) 爻象:上六处解之终,仍有隐患(隼)居高墉,需彻底清除 “获之,无不利”:擒获它,无所不利 历史例证:汉武帝彻底解决诸侯王问题(推恩令),巩固统一 金景芳总结:解卦以“射隼”作结,强调解难的彻底性 六、解卦的解难智慧总论 1. 行动原则:“险以动,动而免乎险” 积极行动,脱出险境 2. 政治方向:“利西南,往得众” 解难后争取民心,稳定大局 3. 善后要务: 肃清余孽(田获三狐) 防止炫耀(负且乘) 解脱民困(解而拇) 感化小人(有孚于小人) 清除顽敌(射隼高墉) 4. 宽恕精神:“赦过宥罪” 但宽恕有度,不是无限赦免 5. 金景芳总结:解卦是儒家“拨乱反正”思想的体现,强调解难要彻底,善后要谨慎,治国要以德服人。
▶
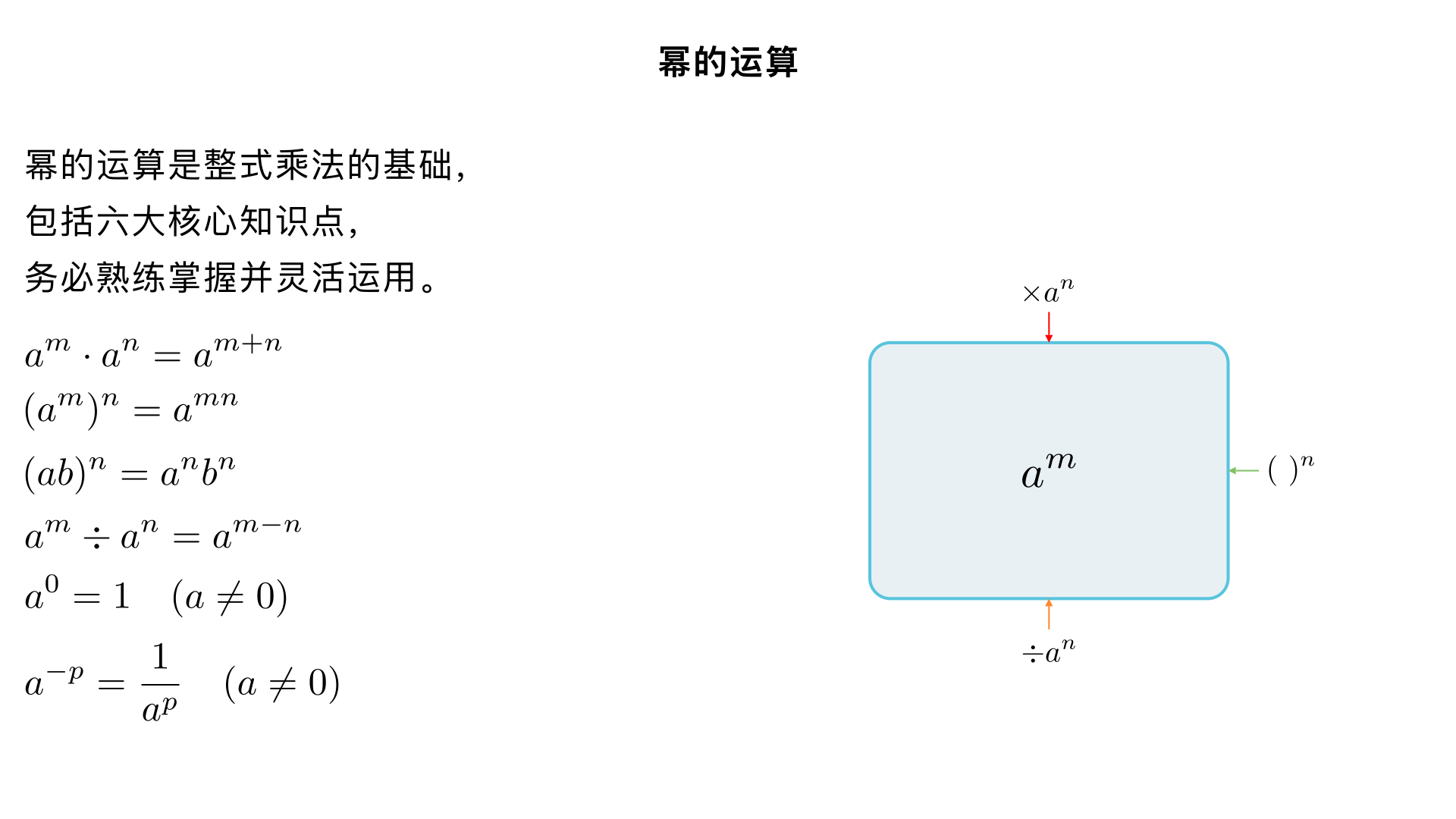
八年级数学 / 整式的乘法 / 幂的运算 幂的运算核心包括同底数幂的乘法、幂的乘方、积的乘方、同底数幂的除法、零指数幂、负整数指数幂六大知识点,是整式乘法的基础,务必熟练掌握并能灵活运用。 一、核心知识点总览 运算类型 核心法则 字母表达式 适用条件 同底数幂的乘法 底数不变,指数相加 a m ⋅a n =a m+n a =0 , m,n 为正整数 幂的乘方 底数不变,指数相乘 (a m ) n =a mn a =0 , m,n 为正整数 积的乘方 积的每一个因式分别乘方,再把所得的幂相乘 (ab) n =a n b n a,b =0 , n 为正整数 同底数幂的除法 底数不变,指数相减 a m ÷a n =a m−n a =0 , m,n 为正整数, m>n 零指数幂 任何不等于 0 的数的 0 次幂都等于 1 a 0 =1 a =0 负整数指数幂 任何不等于 0 的数的 −p 次幂等于它的 p 次幂的倒数 a −p = a p 1 a =0 , p 为正整数 二、分知识点详解 2.1 同底数幂的乘法 法则推导(基于幂的定义): 个 个 个 拓展应用: 三个及以上同底数幂相乘: a m ⋅a n ⋅a p =a m+n+p ( m,n,p 为正整数) 底数可以是单项式或多项式: (x−y) 2 ⋅(x−y) 3 =(x−y) 2+3 =(x−y) 5 逆用公式: a m+n =a m ⋅a n (用于因式分解或简便计算) 例题: 计算: 2 3 ×2 5 =2 3+5 =2 8 =256 计算: a 7 ⋅a 3 =a 7+3 =a 10 逆用: a 5 =a 2+3 =a 2 ⋅a 3 易错点: 底数不同不能直接用此法则: 2 3 ×3 5 =6 8 (需先判断底数是否相同) 指数是 1 时容易忽略: a⋅a 2 =a 1+2 =a 3 ( a=a 1 ) 2.2 幂的乘方 法则推导: 个 拓展应用: 多重乘方: ((a m ) n ) p =a mnp ( m,n,p 为正整数) 逆用公式: a mn =(a m ) n =(a n ) m 例题: 计算: (10 3 ) 5 =10 3×5 =10 15 计算: (a 2 ) 4 =a 2×4 =a 8 逆用: a 12 =(a 3 ) 4 =(a 4 ) 3 =(a 6 ) 2 易错点: 与同底数幂的乘法混淆: (a 3 ) 4 =a 3+4 (幂的乘方是指数相乘,不是相加) 系数未乘方: (2a 3 ) 2 =2a 6 (正确结果: 4a 6 ,系数也要平方) 2.3 积的乘方 法则推导: 个 个 个 拓展应用: 多个因式的积的乘方: (abc) n =a n b n c n ( n 为正整数) 逆用公式: a n b n =(ab) n (用于简便计算) 例题: 计算: (2x) 3 =2 3 ⋅x 3 =8x 3 计算: (−3a 2 b) 4 =(−3) 4 ⋅(a 2 ) 4 ⋅b 4 =81a 8 b 4 逆用: 4 3 ×5 3 =(4×5) 3 =20 3 =8000 易错点: 漏乘方某个因式: (a+b) n =a n +b n (这是完全平方公式,不是积的乘方) 符号错误: (−a) 3 =−a 3 , (−a) 4 =a 4 (奇次幂符号不变,偶次幂符号为正) 2.4 同底数幂的除法 法则推导: 个 个 个 ( m>n ) 拓展应用: 零指数幂:当 m=n 时, a m ÷a n =a 0 =1 ( a =0 ) 负整数指数幂:当 m<n 时, a m ÷a n =a −(n−m) = a n−m 1 ( a =0 ) 例题: 计算: 10 8 ÷10 5 =10 8−5 =10 3 =1000 计算: a 6 ÷a 2 =a 6−2 =a 4 零指数幂: (−2) 0 =1 ( −2 =0 ) 负指数幂: 2 −3 = 2 3 1 = 8 1 易错点: 底数为 0 无意义: 0 0 和 0 −p 都没有意义 负指数幂的运算顺序: 2a −1 =(2a) −1 (正确: 2a −1 = a 2 ) 2.5 幂的混合运算技巧 运算顺序: 先算乘方,再算乘除,最后算加减 有括号的先算括号里面的 同级运算从左到右依次进行 常用技巧: 化异底为同底:如 (−a) 2 =a 2 , (a−b) 3 =−(b−a) 3 逆用法则:灵活运用 a m+n =a m ⋅a n 、 a mn =(a m ) n 、 a n b n =(ab) n 进行简便计算 符号处理:先判断结果的符号,再计算绝对值 综合例题: 计算: (2a 2 b) 3 ⋅(3ab 2 ) 2 解:原式 =8a 6 b 3 ⋅9a 2 b 4 =72a 6+2 b 3+4 =72a 8 b 7 计算: (x 3 ) 4 ÷(x 2 ) 5 解:原式 =x 12 ÷x 10 =x 12−10 =x 2 简便计算: (− 2 1 ) 2023 ×2 2024 解:原式 =(− 2 1 ) 2023 ×2 2023 ×2=(−1) 2023 ×2=−2 三、巩固练习(附答案) 基础题(直接运用法则) $a^3 \cdot a^5 = ( 答 案 : a^8$) $(x^2)^4 = ( 答 案 : x^8$) $(3xy)^2 = $______(答案: 9x 2 y 2 ) $10^7 \div 10^3 = $______(答案: 10 4 ) $(-5)^0 = $______(答案:1) $3^{-2} = ( 答 案 : \frac{1}{9}$) 提高题(混合运算) $(a^2)^3 \cdot a^4 = ( 答 案 : a^{10}$) $(2a^3b)^2 \div (ab)^3 = $______(答案: 4a 3 b −1 = b 4a 3 ) $(-a)^3 \cdot (a^2)^5 = ( 答 案 : -a^{13}$) $(x-y)^3 \cdot (y-x)^2 = ( 答 案 : (x-y)^5$) 拓展题(逆用法则) 若 a m =2 , a n =3 ,则$a^{m+n} = $______(答案:6) 若 a m =2 ,则$a^{3m} = $______(答案:8) 计算:$0.125^{2023} \times 8^{2023} = $______(答案:1) 四、学习建议 理解本质:幂的运算都是基于 “几个相同因数相乘” 的定义推导而来,理解法则的推导过程比死记硬背更重要 区分法则:重点区分 “同底数幂相乘(指数相加)” 与 “幂的乘方(指数相乘)”,避免混淆 多做练习:从基础题到混合运算,逐步提高难度,培养运算能力 总结易错点:建立错题本,记录常见错误(如符号错误、底数不同误用法则等),定期复习 核心口诀:同底相乘,指数相加;幂的乘方,指数相乘;积的乘方,各因式分别乘方;同底相除,指数相减;零次幂为 1,负次幂为倒数。
▶
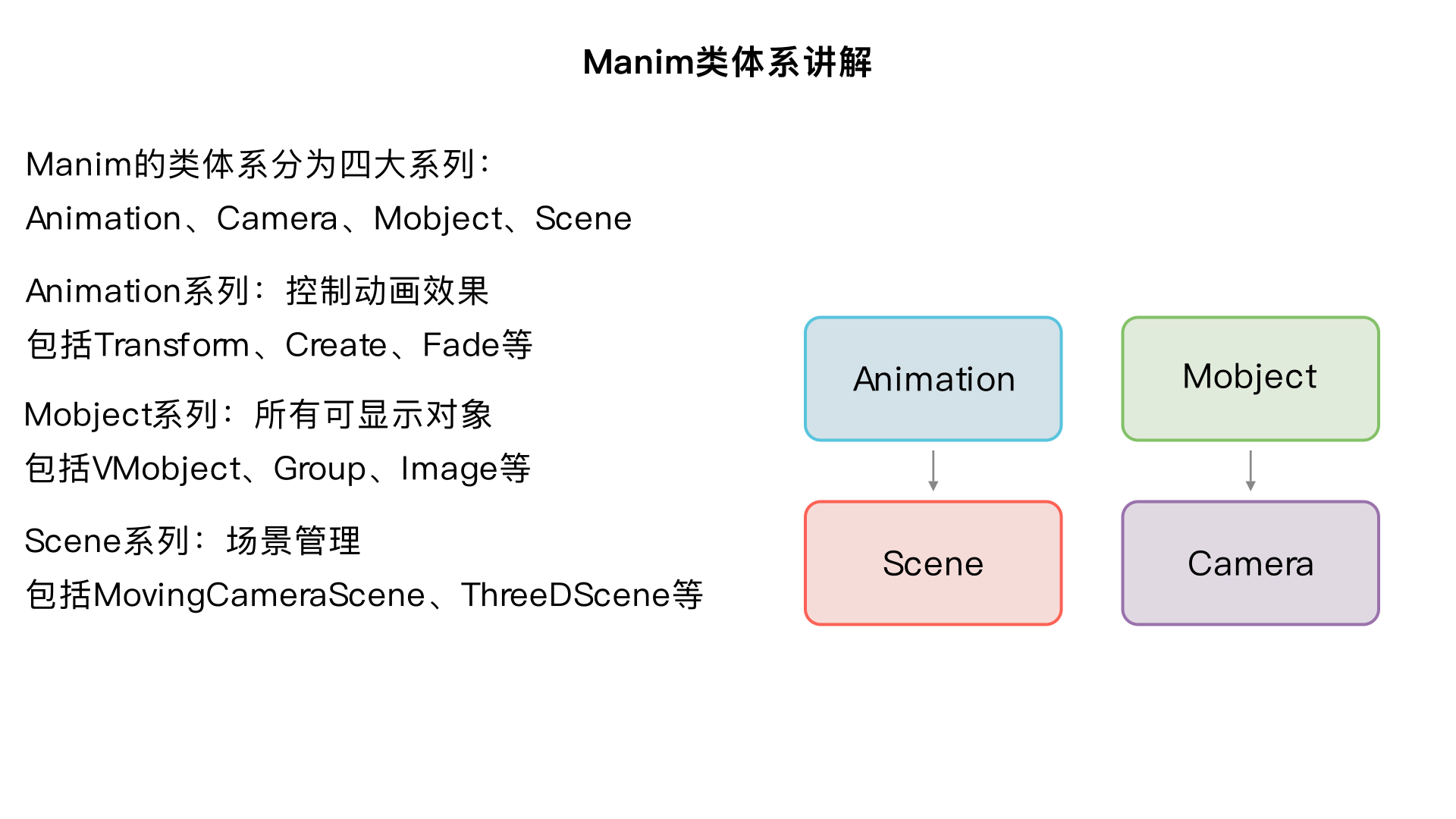
下面给出一种 **可阅读、可查阅、可作为字典使用的 Manim 类讲解**。 你给出的继承图包含 **Animation 系列、Camera 系列、Mobject 系列、Scene 系列**。这些类总数非常大,如果逐条硬性解释会变成极长的文档,不利于阅读。因此下面采用: 1. **按功能分类解释整个体系的设计思路与用途** 2. **对每个类给出它的作用、典型使用场景、是否常用** 3. **同一类型中,先解释父类,再解释子类,帮助理解继承结构** 若你之后希望对“某一类”“某一段继承链”“某类用途示例”“按图创造动画”等,我可以继续展开。 --- # 一、Animation 动画类体系讲解 Manim 的 Animation 是所有动画的根类。 动画类的继承链大致分为: ## 1.1 Animation(根类) 所有动画的基类,提供: * 动画持续时间 * 插值方式 * 钩子函数(begin / update / finish) 多数子类只需要实现 `interpolate_mobject`。 --- ## 1.2 Transform 系列(改变物体形状/位置的核心类) ### **Transform** 将一个 Mobject 变换到另一个 Mobject。 常用于移动、形变、交换结构。 ### **ReplacementTransform** 在变换过程中“替换”旧物体。常用于文字替换。 ### **TransformFromCopy** 用复制品开始变换,不影响原对象。 ### **CyclicReplace** 循环交换多个对象位置。 ### **Swap** 两个对象交换。 ### **ApplyMethod** 执行某个 mobject 的方法,如 `ApplyMethod(mob.shift, RIGHT)`。 ### **ApplyFunction** 用函数改变 mobject 上所有点的位置。 ### **ApplyPointwiseFunction / ToCenter** 作用于每个点。ToCenter 是把点位置映射到以中心为基准的变换。 ### **ApplyComplexFunction** 把平面上的点视为复数进行变换。 ### **MoveToTarget** 与 `.generate_target()` 配套,将对象移动到自定义 target。 ### **ClockwiseTransform / CounterclockwiseTransform** 绕中心点的旋转方向。 ### **Rotate** 旋转指定角度。 ### **GrowFromCenter / GrowFromEdge / GrowFromPoint** 从点 / 边 / 中心处“生长”出来。 ### **Indicate / FocusOn** 强调某物体(放大、颜色闪烁)。 ### **FadeTransform / FadeTransformPieces** 伴随淡出与淡入的变换。 --- ## 1.3 Create 与 ShowPartial 系列(绘制路径) ### **Create** 沿轮廓绘制一个 VMobject(如文字、公式、线条) ### **Uncreate** Create 的逆过程 ### **ShowPartial / ShowIncreasingSubsets** 逐渐显示子集或路径,用于路径型图形。 --- ## 1.4 Fade 系列(透明度变化) ### **FadeIn / FadeOut** 淡入淡出 ### **FadeToColor** 逐渐变成某种颜色 --- ## 1.5 Boundary / Flash / Wiggle 等效果类 ### **AnimatedBoundary** 显示物体边界的流动光效 ### **Flash** 闪光效果 ### **Wiggle** 轻微抖动强调 --- ## 1.6 群组动画类 ### **AnimationGroup** 多个动画并列执行 ### **Succession** 多个动画按顺序执行 ### **LaggedStart / LaggedStartMap** 对象列表逐个延迟开始动画(如“一组点依次出现”) ### **Broadcast** 波纹扩散效果 --- ## 1.7 数字动画 ### **ValueTracker / ChangingDecimal / ChangeDecimalToValue** 数值随时间改变。 --- ## 1.8 特殊效果类 ### **Homotopy / ComplexHomotopy / ApplyWave** 基于映射函数的高自由度变形 ### **MoveAlongPath** 沿既定路径移动(常用于箭头或点沿曲线移动) ### **SpiralIn** 螺旋入场 ### **Wait** 暂停 --- --- # 二、Camera 摄像机类体系 Camera 负责渲染世界到画面中。 ## **Camera(根类)** 二维摄像机。Scene 默认使用它。 ### **MovingCamera** 允许修改 frame(摄像机视野框) ### **MultiCamera / OldMultiCamera / SplitScreenCamera** 用于将多个画面整合到一个输出里,如分屏效果。 ### **MappingCamera** 把画面映射到某种复杂的变换(如扭曲) ### **ThreeDCamera** 用于 3D 场景(透视投影、旋转等) ### **BackgroundColoredVMobjectDisplayer** 处理背景色图层的渲染 --- --- # 三、Mobject(所有可显示对象的基类) Mobject 是 Manim 场景中“一切可显示物体”的根类。 分成数个大类: # 3.1 VMobject(矢量图对象) Vectorized Mobject,基于路径的可缩放矢量图形。 ## 常见子类: ### **Line / DashedLine / TangentLine** 直线、虚线、切线 ### **Circle / Ellipse / Annulus / Sector** 圆与相关形状 ### **Polygon / Polygram / Star** 多边形结构 ### **Arc / ArcBetweenPoints / ArcPolygon** 弧线结构 ### **Brace / BraceLabel** 用来标注区间的方括号 ### **Arrow / CurvedArrow / DoubleArrow** 箭头 ### **Tex / MathTex** 渲染 LaTeX 公式 ### **Text / MarkupText** 渲染文本(SVG 或 Markup) ### **Table / DecimalTable / MobjectTable** 表格 ### **Axes / NumberPlane / ThreeDAxes / PolarPlane** 坐标系 ### **FunctionGraph / ParametricFunction** 函数图像 ### **Vector / VectorField / StreamLines** 向量与场 ### **Surface / Sphere / Cone / Cylinder / Torus** 曲面与 3D 图形 ### **Dot / Point / PointCloudDot** 点类对象 ### **ValueTracker / ComplexValueTracker / Variable** 数值跟踪器,用于驱动动画 --- # 3.2 Group / VGroup 容器类,把多个 Mobject 组合成一个整体。 --- # 3.3 Image 类 ### **ImageMobject / AbstractImageMobject / ImageMobjectFromCamera** 用位图图像渲染(如 PNG) --- # 3.4 Polyhedron 系列 多面体:Cube、Prism、Tetrahedron、Octahedron、Icosahedron、Dodecahedron --- # 3.5 Figure / Diagram 系类 DiGraph、Graph、SampleSpace 等更特殊的可视化对象。 --- --- # 四、Scene 场景类体系 Scene 是 Manim 的核心执行单元。 ## **Scene(根类)** 负责: * 设置摄像机 * 渲染动画 * 帧管理 --- ## 4.1 Camera 扩展类场景 ### **MovingCameraScene** 使摄像机视野框可移动 ### **ZoomedScene** 带局部放大视野 --- ## 4.2 3D 场景 ### **ThreeDScene** 支持三维摄像机旋转、光照等。 ### **SpecialThreeDScene** 额外的三维效果。 --- ## 4.3 专用数学类场景 ### **VectorScene** 向量投影、线性代数可视化 ### **LinearTransformationScene** 展示线性变换(矩阵作用) --- # 五、总结与使用建议 如果你的目标是: * **做公式演示** → `MathTex` + `Write` + `TransformMatchingTex` * **做图形变换** → `Transform / ReplacementTransform / ApplyMethod` * **制作流程动画** → `AnimationGroup / Succession / LaggedStart` * **绘制曲线** → `ParametricFunction / FunctionGraph` * **做 3D 可视化** → `ThreeDScene + Surface 系列` * **制作坐标系** → `Axes / NumberPlane`
▶
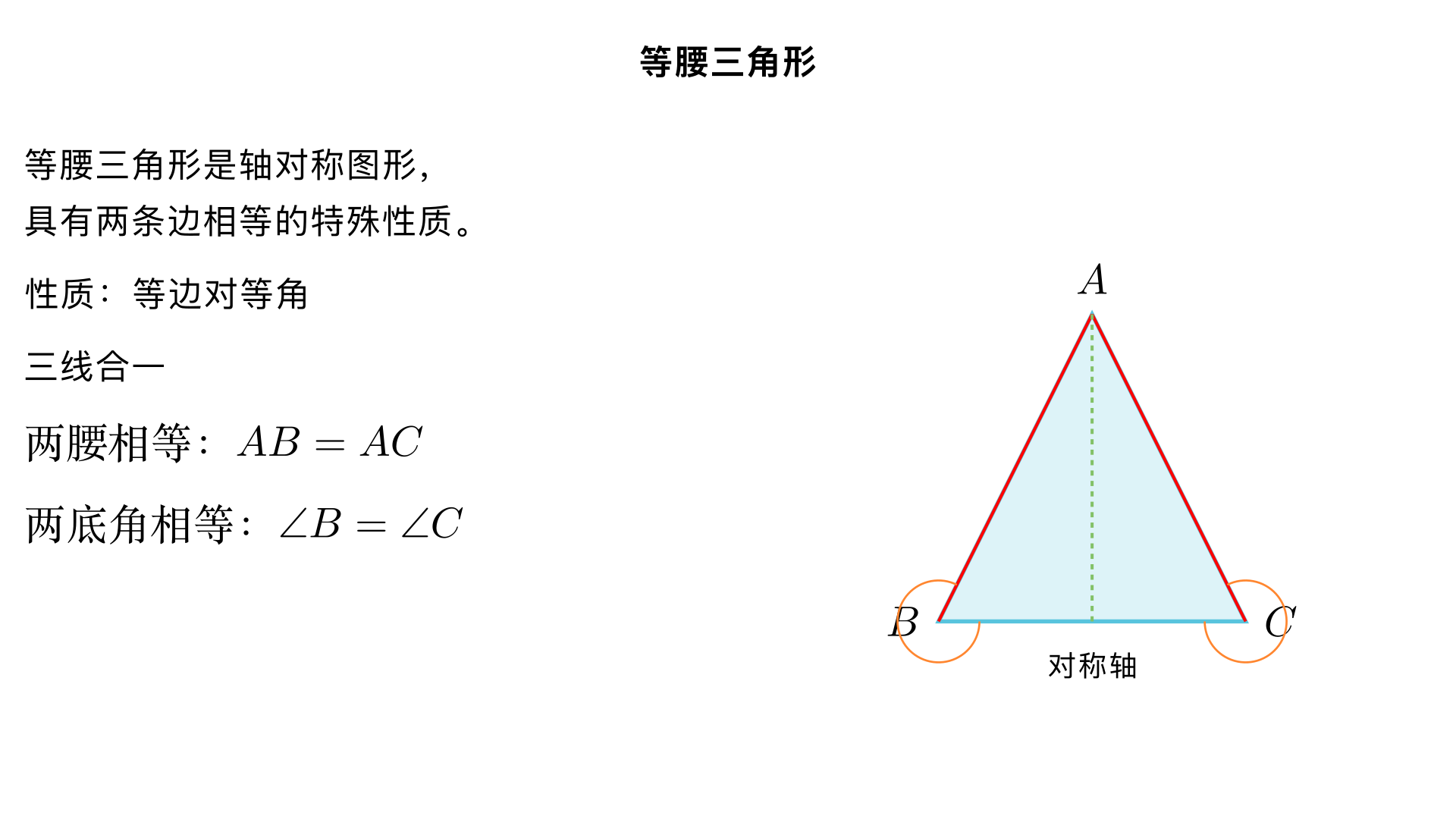
八年级数学 / 轴对称 / 等腰三角形 一、核心知识点(精炼版) 1. 定义 有两条边相等的三角形叫做等腰三角形(相等的边为腰,第三边为底边;两腰的夹角为顶角,腰与底边的夹角为底角)。 2. 性质(中考高频) 轴对称性:等腰三角形是轴对称图形,对称轴为底边的垂直平分线(1 条)。 边的性质:两腰相等(已知条件推导核心)。 角的性质:等边对等角(两底角相等,∠B=∠C)。 三线合一:等腰三角形的顶角平分线、底边的中线、底边的高重合(3 条线共 1 条,需满足 “顶角平分线”“底边相关” 两个前提)。 3. 判定 定义法:有两条边相等的三角形是等腰三角形。 角的判定:等角对等边(如果一个三角形有两个角相等,那么这两个角所对的边相等)。 4. 特殊情况:等边三角形(特殊的等腰三角形) 定义:三条边都相等的三角形。 性质: 三个角都相等,且均为 60°; 有 3 条对称轴(每条边的垂直平分线); 满足 “三线合一”(每条边对应的中线、高、对角平分线重合)。 判定: 三条边都相等; 三个角都相等(均为 60°); 有一个角是 60° 的等腰三角形(重点:无需再证三边相等)。
▶
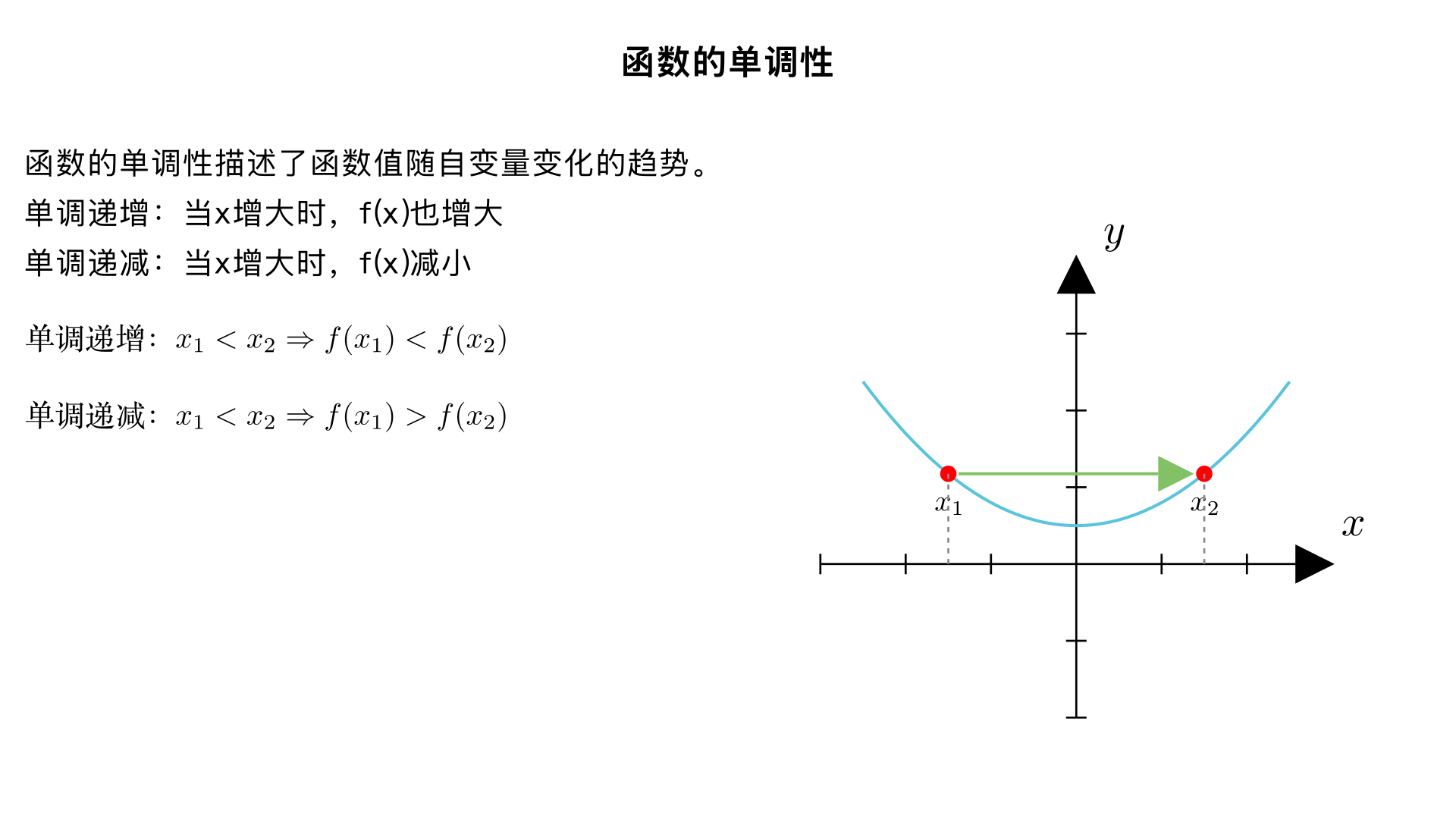
解释一下函数的单调性
▶