T
Teach Me AnythingTMA
Video History
Page 9 / 43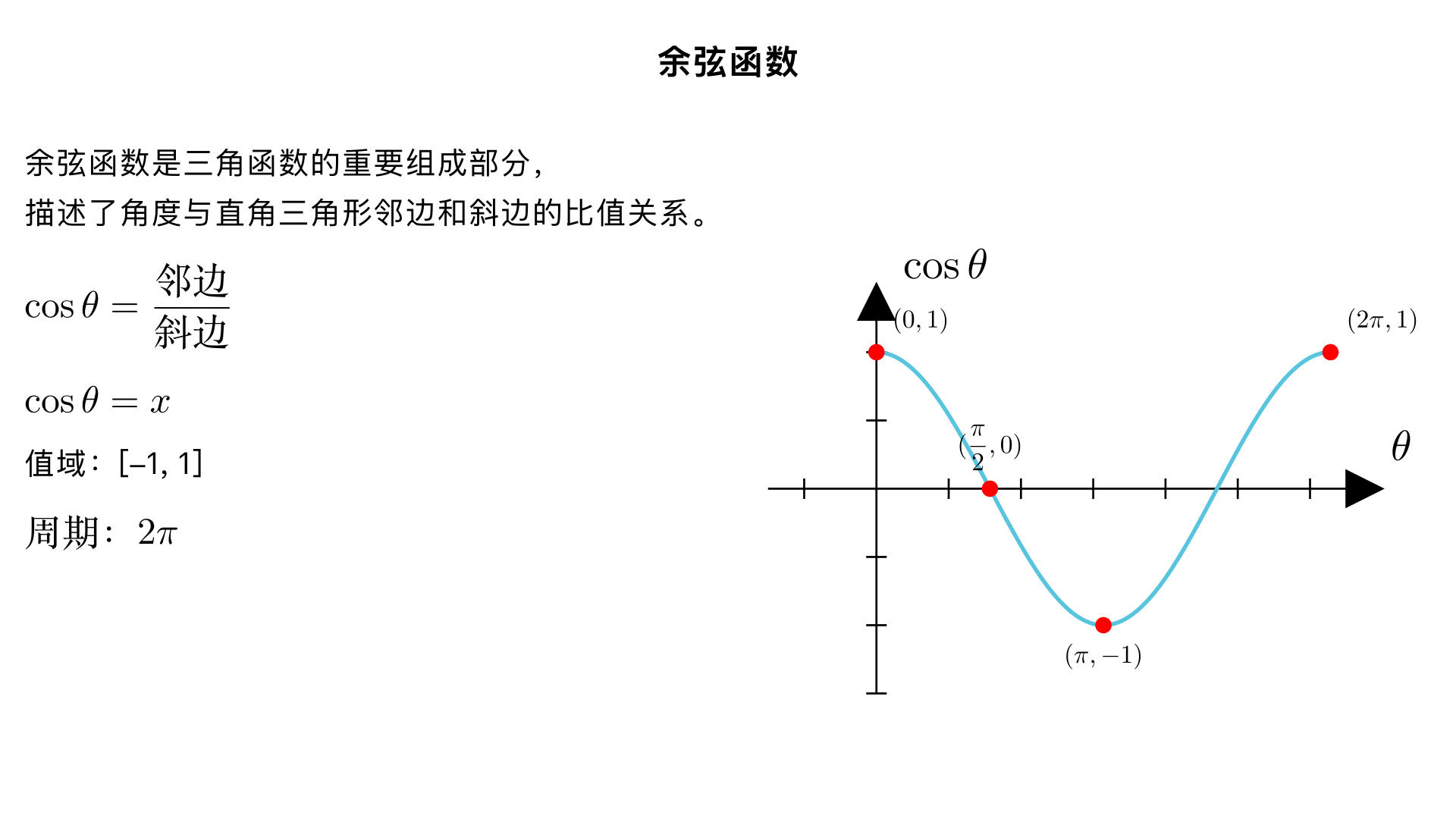
▶
请描述余弦函数
▶
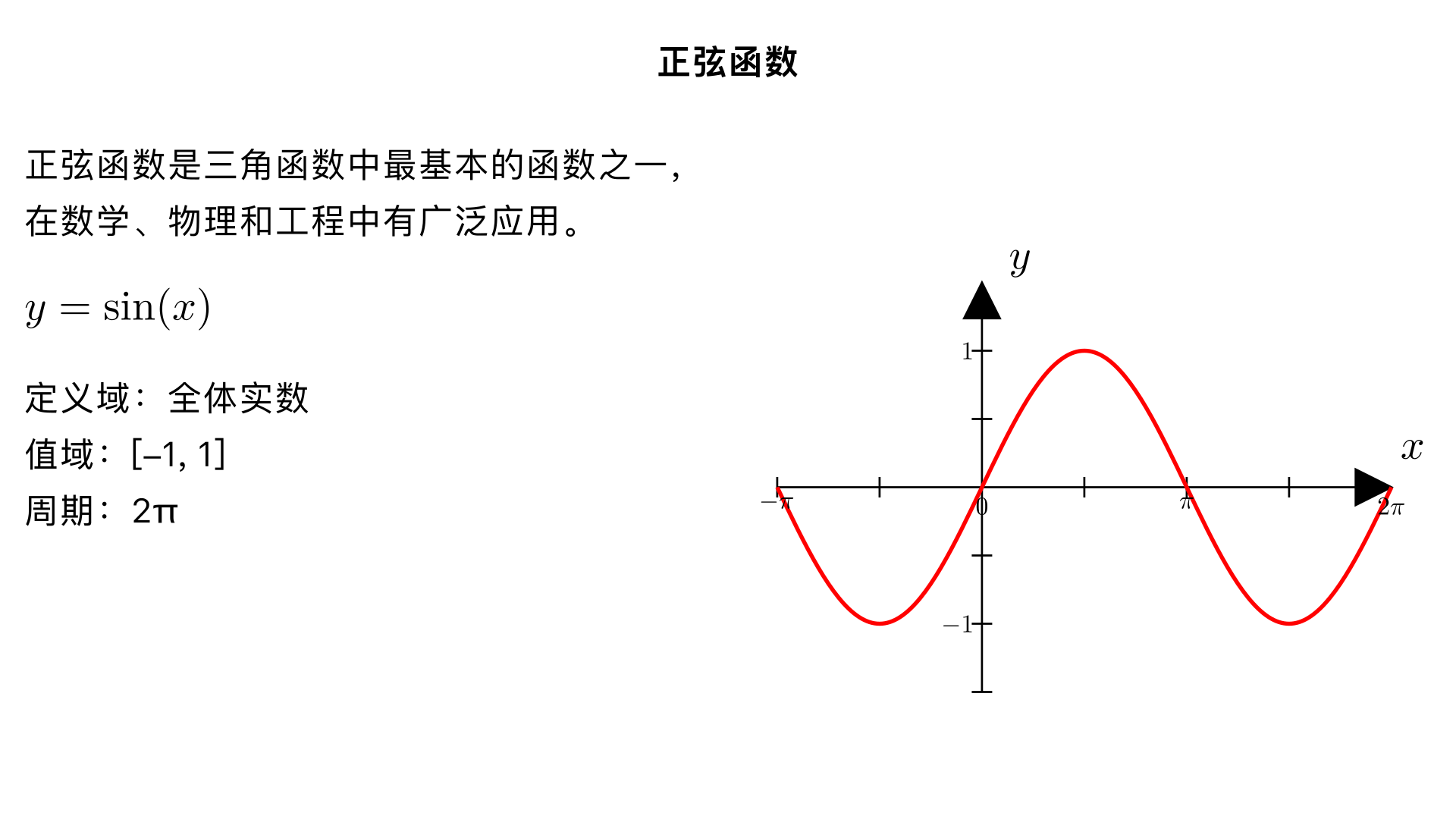
请给我输出正弦函数
▶
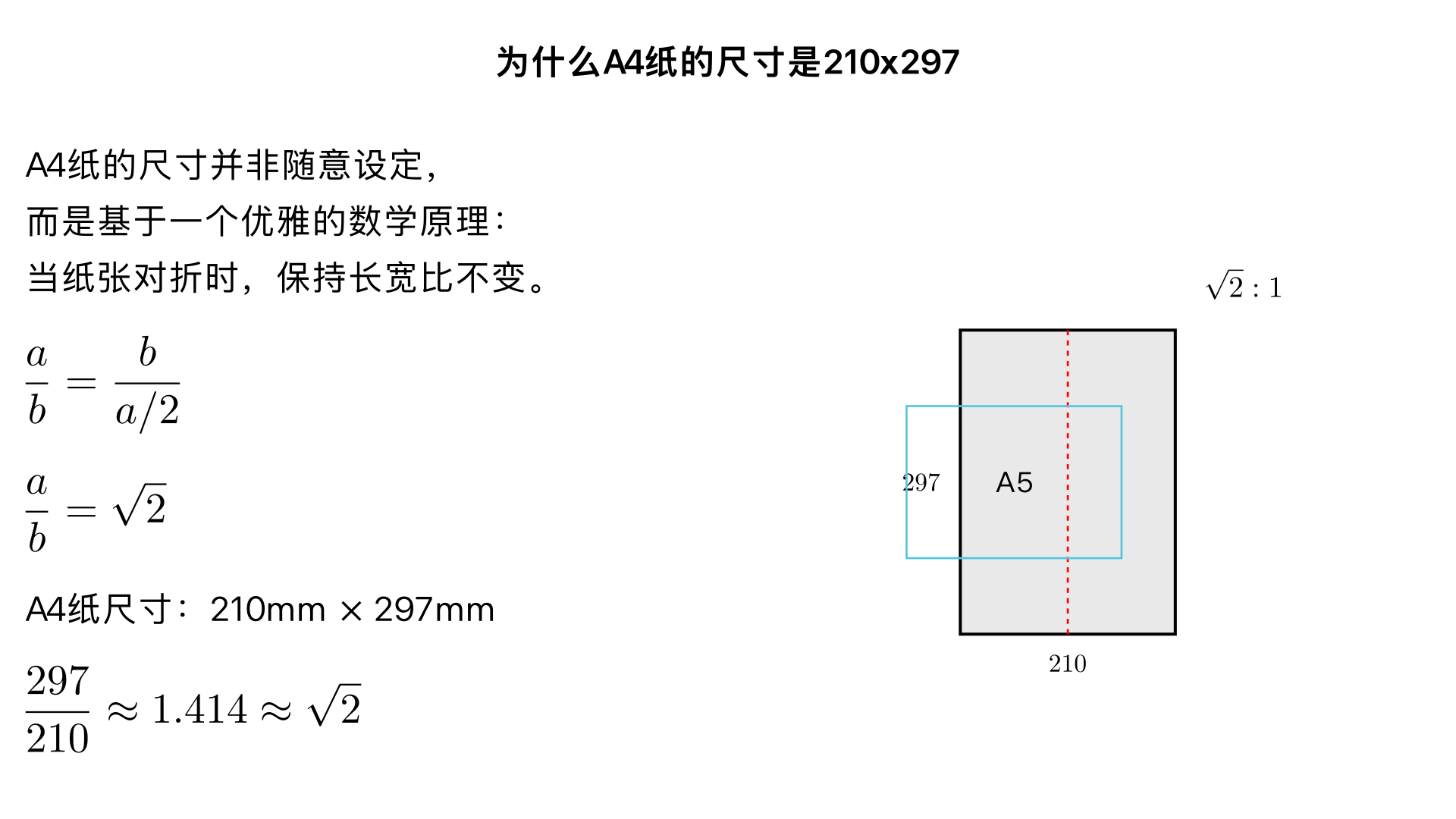
为什么A4纸的尺寸是210x297
▶
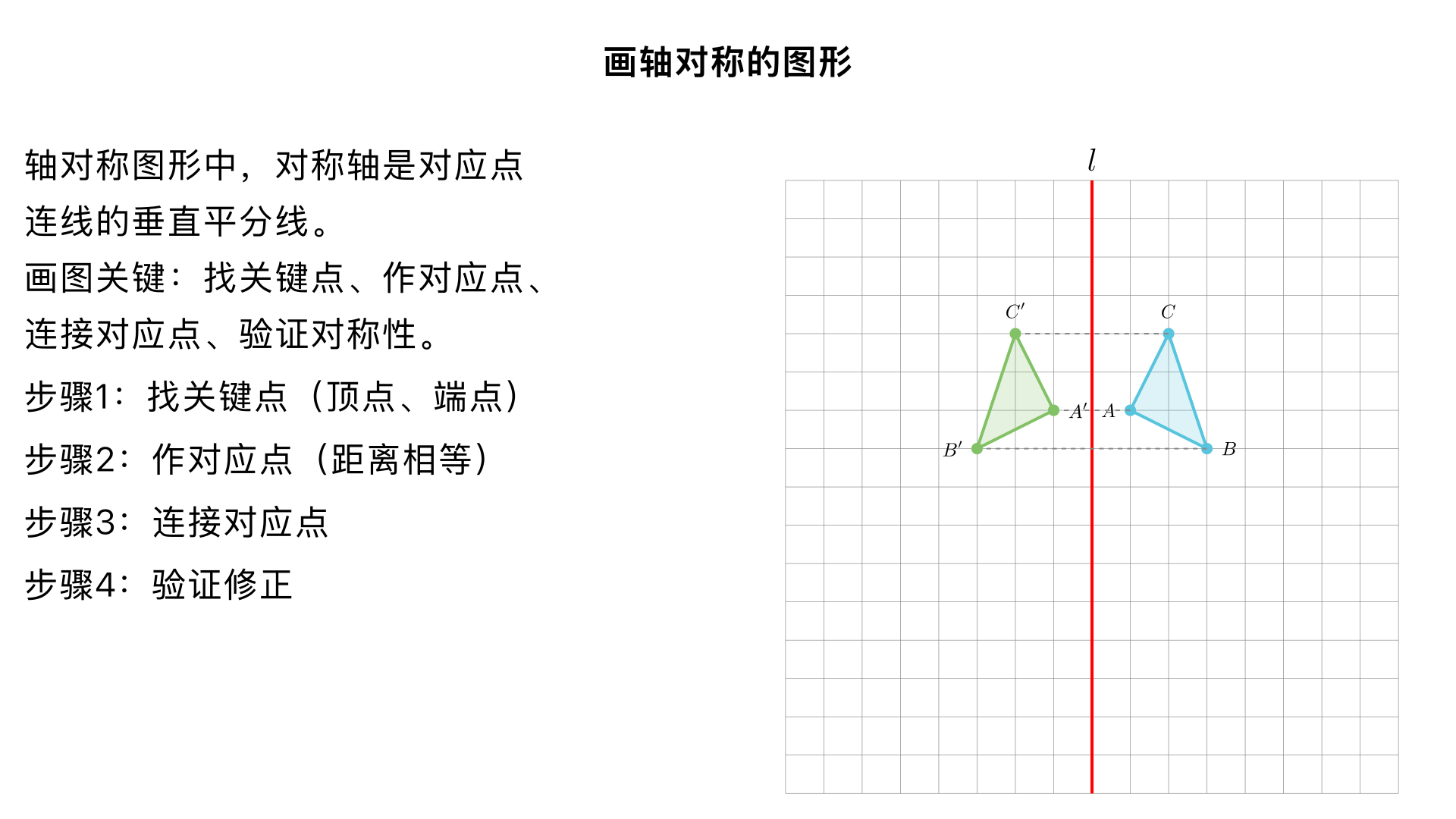
八年级数学 / 轴对称 / 画轴对称的图形 一、核心知识点(5 分钟掌握) 画图依据:轴对称图形中,对称轴是对应点连线的垂直平分线(对应点到对称轴的距离相等,连线与对称轴垂直)。 关键概念: 关键点:图形的顶点、端点、交点(如三角形的 3 个顶点、线段的端点)。 对应点:原图形上的点关于对称轴的对称点。 二、规范画法步骤(以平面图形为例,8 分钟实操) 1. 准备工具 直尺(画直线、量距离)、圆规(画垂直平分线、量等距)、铅笔、纸。 2. 四步画法 步骤 操作细节 ① 找关键点 在原图形上标出所有关键点(如四边形标 4 个顶点,记为 A、B、C、D)。 ② 作对应点 以每个关键点为对象,作关于对称轴 l 的对称点: 1. 过点 A 作直线 l 的垂线(用圆规画弧,交 l 于两点,再作垂直平分线); 2. 在垂线上量取与 A 到 l 相等的距离,得到对称点 A'(确保 A 到 l 的距离 = A' 到 l 的距离); 3. 重复上述操作,得到 B'、C'、D'。 ③ 连对应点 用直尺依次连接 A'、B'、C'、D'(按原图形的顶点顺序连接,避免错乱)。 ④ 验证修正 检查:对应点连线是否垂直于对称轴,对应边长度是否相等,确保图形对称。 3. 网格图简化画法(无圆规时,3 分钟快速画) 若图形在方格纸中,关键点坐标可直接推导: 对称轴为竖直方向(如 x=2):对应点横坐标 = 2×2 - 原横坐标,纵坐标不变(例:A (1,3)→A'(3,3)); 对称轴为水平方向(如 y=1):对应点纵坐标 = 2×1 - 原纵坐标,横坐标不变(例:B (4,2)→B'(4,0))。 三、易错点警示(3 分钟规避) 漏找关键点:忽略线段端点或图形交点,导致对称图形残缺; 距离不等:作对应点时,未量准与对称轴的距离,导致图形不对称; 连线错乱:连接对应点时顺序与原图形不一致,形成 “扭曲图形”; 垂线不垂直:未用圆规规范作垂线,仅凭目测画,导致对应点偏差。 四、典型例题(5 分钟练习 + 解析) 例题:在方格纸中,画出△ABC 关于直线 l 的对称图形(如图,A (1,2)、B (3,1)、C (2,4),对称轴 l 为直线 x=4)。 解析步骤: 确定关键点:A、B、C 三点; 求对应点坐标: A'(2×4 -1, 2)=(7,2); B'(2×4 -3, 1)=(5,1); C'(2×4 -2, 4)=(6,4); 连接 A'、B'、C',得到对称△A'B'C'。 五、即时练习(10 分钟巩固) 基础题:画出边长为 3cm 的正方形关于其竖直中线的对称图形(用圆规 + 直尺规范画); 提升题:在方格纸中,画出梯形 ABCD(A (0,0)、B (4,0)、C (3,2)、D (1,2))关于直线 y=3 的对称图形,写出对应点坐标。
▶
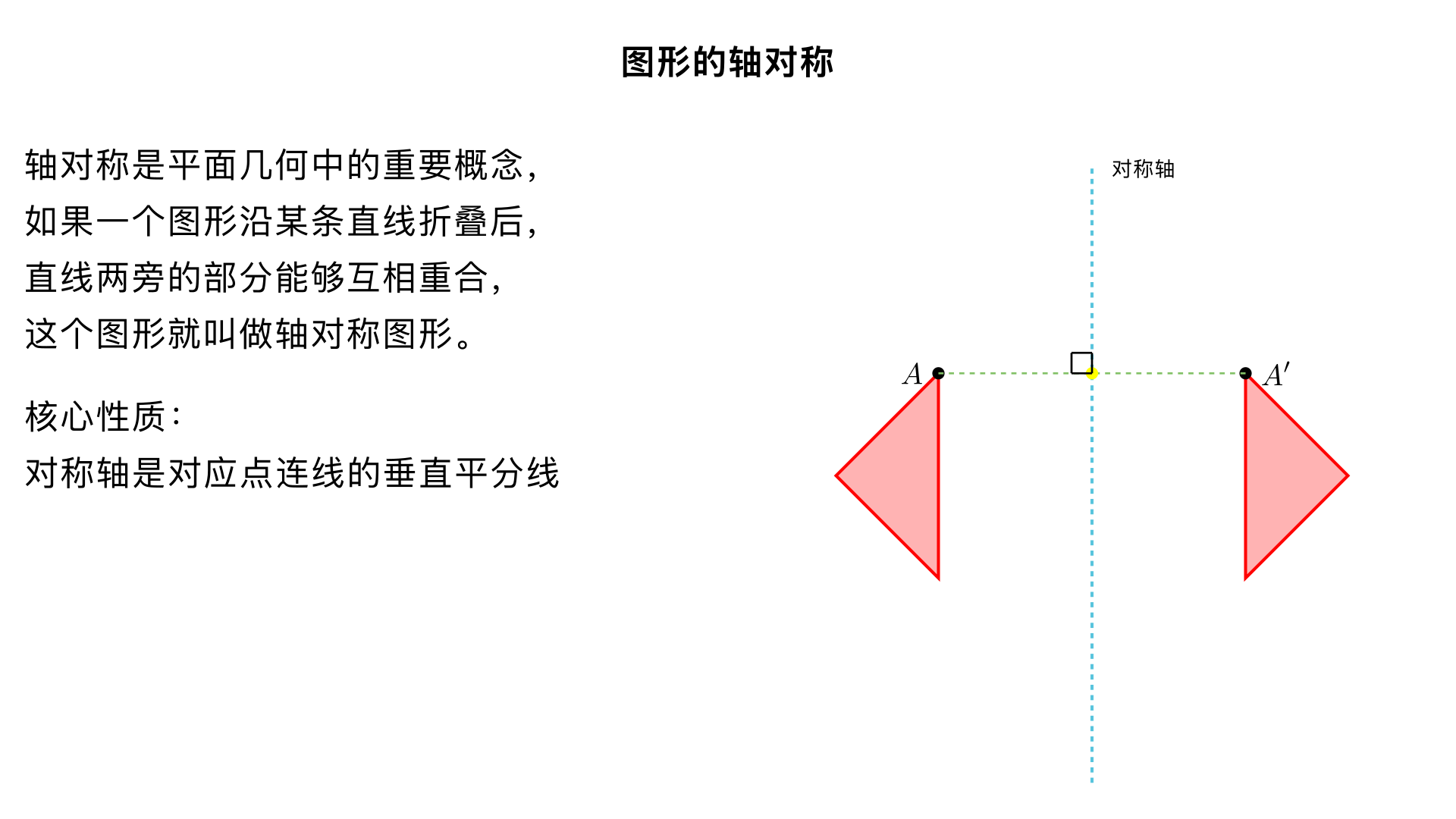
八年级数学 / 轴对称 / 图形的轴对称 一、核心概念(关键定义) 1. 轴对称图形 定义:如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴,折叠后重合的点是对称点(对应点)。 要点: 研究对象是一个图形的自身对称关系 对称轴是直线,不是线段或射线 一个轴对称图形的对称轴可能有一条或多条 2. 两个图形成轴对称 定义:把一个平面图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称,这条直线叫做对称轴,折叠后重合的点是对称点(对应点)。 要点: 研究对象是两个图形之间的对称关系 这两个图形是全等图形 对应点所连线段被对称轴垂直平分 3. 两者区别与联系 项目 轴对称图形 两个图形成轴对称 图形个数 1 个 2 个 对称关系 自身对称 两个图形之间对称 对称轴 1 条或多条 1 条 联系 都沿直线折叠后重合;对称轴都是对应点连线的垂直平分线;把成轴对称的两个图形看成一个整体,就是轴对称图形 二、轴对称的性质(核心定理) 全等性:成轴对称的两个图形是全等图形,对应边相等,对应角相等。 垂直平分线性质:对称轴是任何一对对应点所连线段的垂直平分线(核心性质)。 对应关系: 对应线段相等,对应线段所在直线的交点在对称轴上(或平行于对称轴) 对应角相等,对应角的两边关于对称轴对称 对称性:轴对称变换不改变图形的形状和大小,只改变图形的位置。 三、常见轴对称图形及对称轴数量 图形 对称轴数量 对称轴描述 线段 2 条 线段的垂直平分线;线段所在的直线 角 1 条 角平分线所在的直线 等腰三角形 1 条 顶角平分线(底边上的高、底边上的中线)所在直线 等边三角形 3 条 每条边上的高(中线、所对角的平分线)所在直线 矩形 2 条 对边中点连线所在直线 菱形 2 条 对角线所在直线 正方形 4 条 对边中点连线 + 两条对角线所在直线 圆 无数条 过圆心的任意直线 正 n 边形 n 条 每条边的垂直平分线(或每个内角的平分线)所在直线 四、对称轴的画法(操作步骤) 找对称点:在图形上选取若干个关键点(顶点、端点等) 作垂线:过每个关键点作对称轴的垂线 量距离:在垂线上截取与该点到对称轴距离相等的线段 连对称点:依次连接所有对称点,得到对称图形 五、轴对称的判定(识别方法) 定义法:沿某条直线折叠后,直线两旁部分完全重合 性质法: 若两个图形的对应点连线都被同一条直线垂直平分,则这两个图形成轴对称 若一个图形的所有点关于某条直线的对称点都在该图形上,则该图形是轴对称图形 六、典型例题与应用 例题 1:基础识别 下列图形中,是轴对称图形的有( )① 等腰三角形 ② 平行四边形 ③ 矩形 ④ 梯形 ⑤ 圆答案:①③⑤(解析:平行四边形无对称轴,一般梯形无对称轴) 例题 2:性质应用 已知△ABC 与△A'B'C' 关于直线 l 对称,AB=5cm,∠A=60°,则 A'B'=,∠A'=答案:5cm,60°(解析:成轴对称的图形对应边相等,对应角相等) 例题 3:作图题 已知线段 AB 和直线 l,画出线段 AB 关于直线 l 的对称线段 A'B'步骤: 过 A 作 l 的垂线,垂足为 O,延长 AO 到 A',使 OA'=OA 过 B 作 l 的垂线,垂足为 P,延长 BP 到 B',使 PB'=PB 连接 A'B',即为所求对称线段 七、易错点与注意事项 对称轴类型:对称轴是直线,不是线段或射线(如角的对称轴是角平分线所在直线,不是角平分线本身) 线段对称轴:线段有两条对称轴,不要漏掉线段所在直线 等腰三角形:对称轴是顶角平分线所在直线,也是底边上的高和中线所在直线(三线合一) 区分概念:不要混淆 “轴对称图形” 和 “两个图形成轴对称” 的概念 八、知识拓展 轴对称变换:由一个图形得到它的轴对称图形的过程叫做轴对称变换,属于全等变换 最短路径问题:利用轴对称性质解决(如 “将军饮马” 问题) 对称美:轴对称图形在建筑、艺术、设计等领域有广泛应用(如故宫、天坛等建筑) 核心口诀:轴对称,很重要,折叠重合是关键。一个图形叫对称,两个图形成轴对称。对称轴是垂直平分线,对应边等角不变。
▶
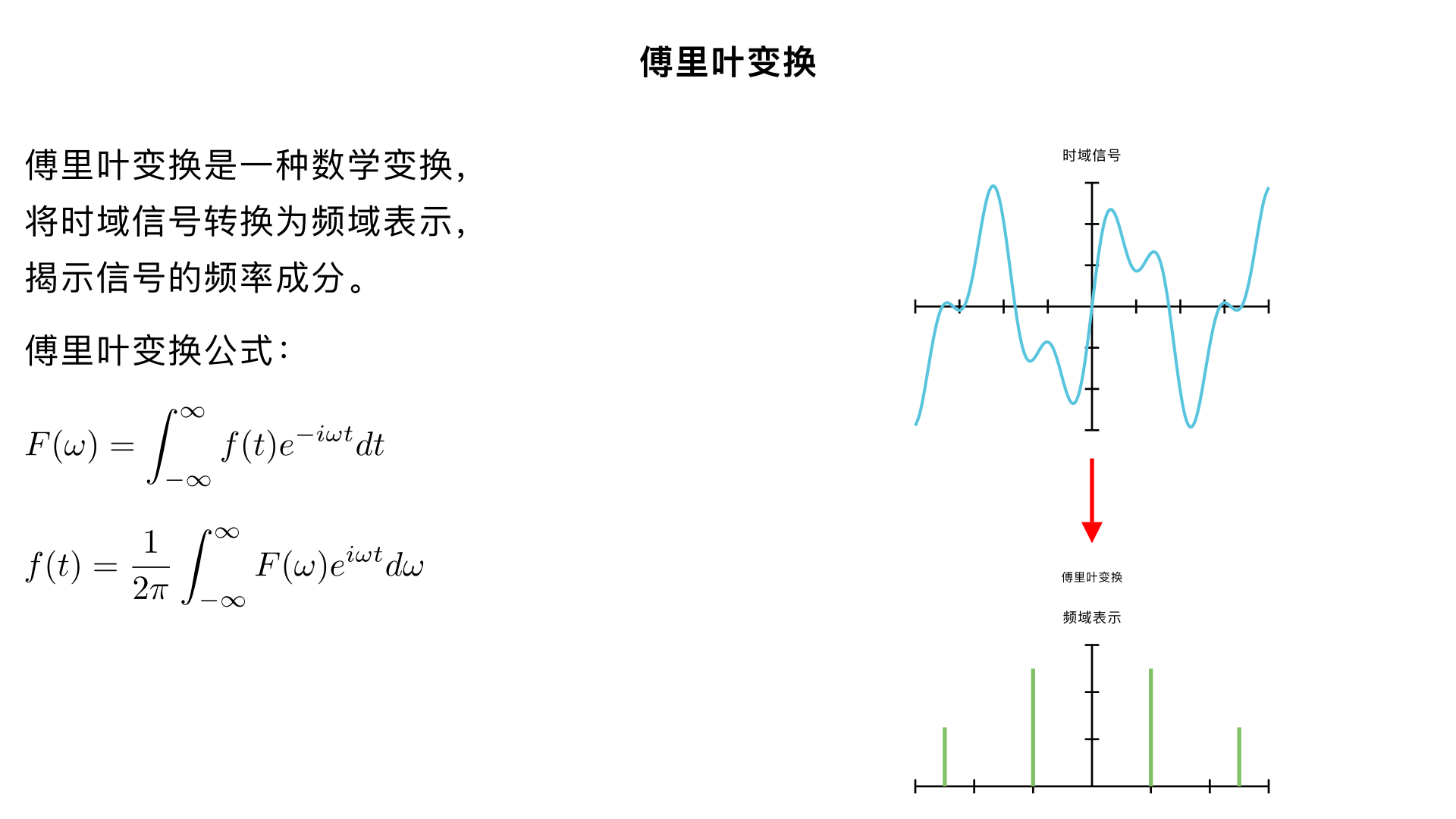
请描述傅里叶变换
▶
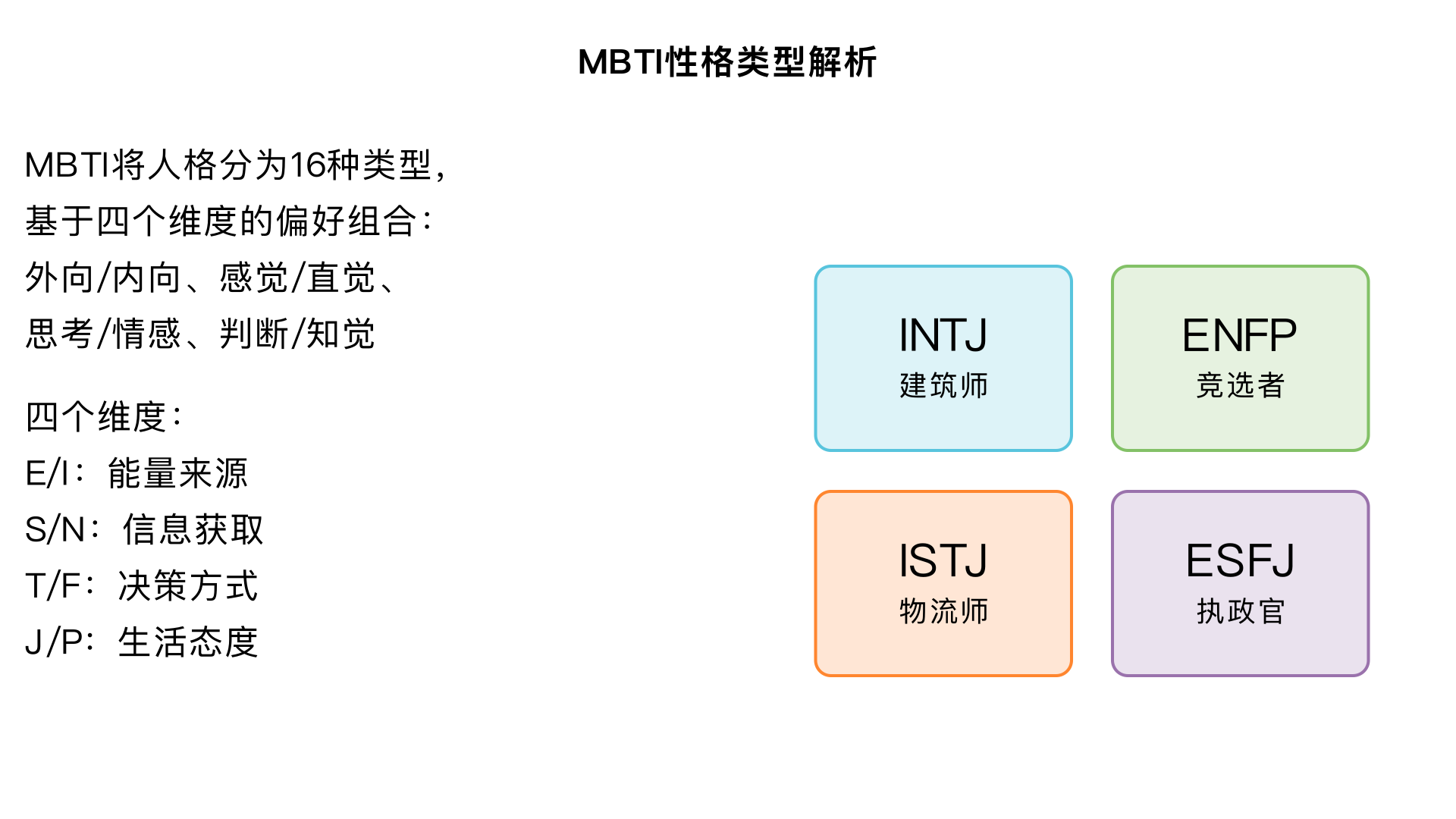
mbti各种性格解释
▶
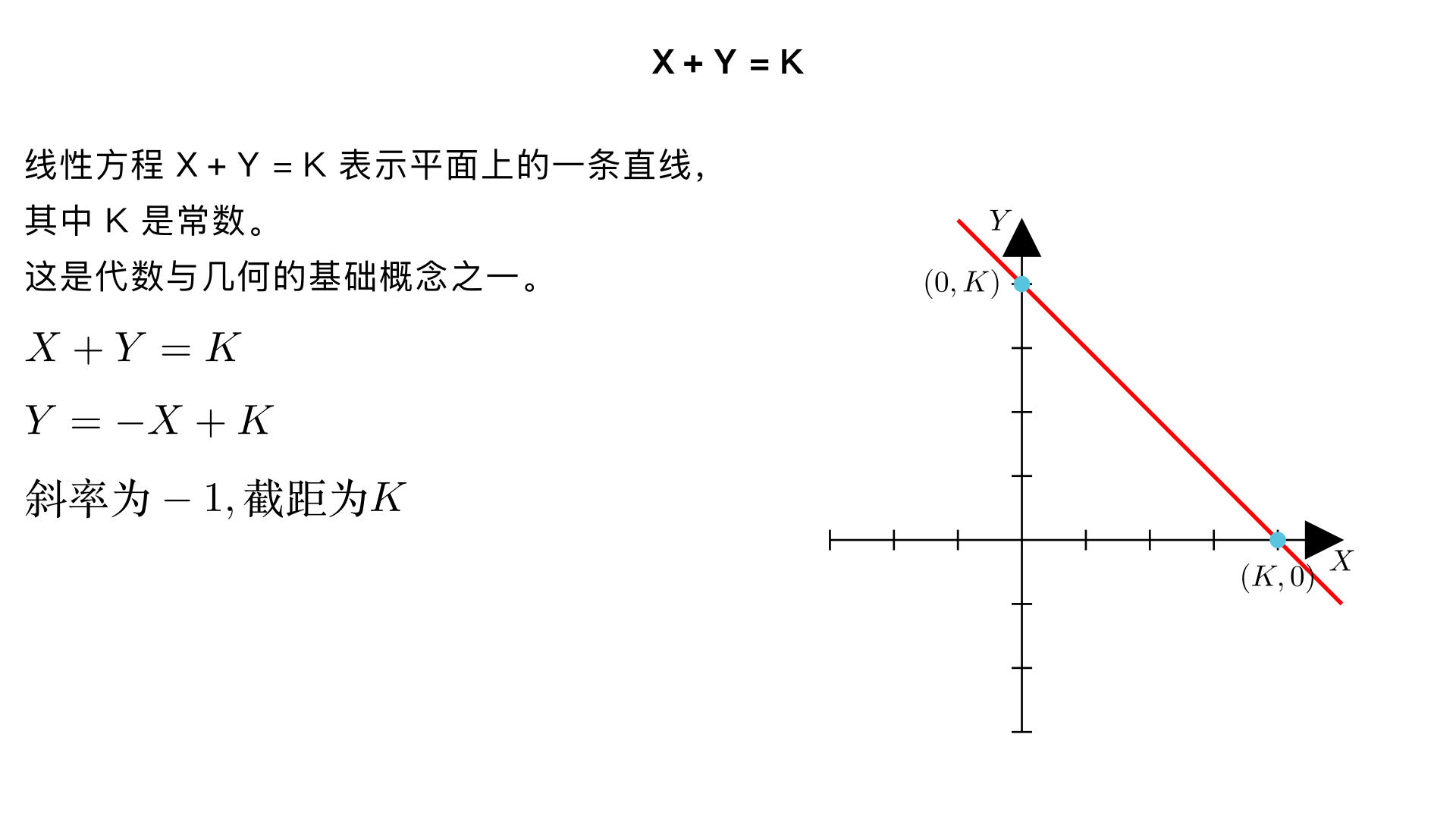
X + Y = K
▶
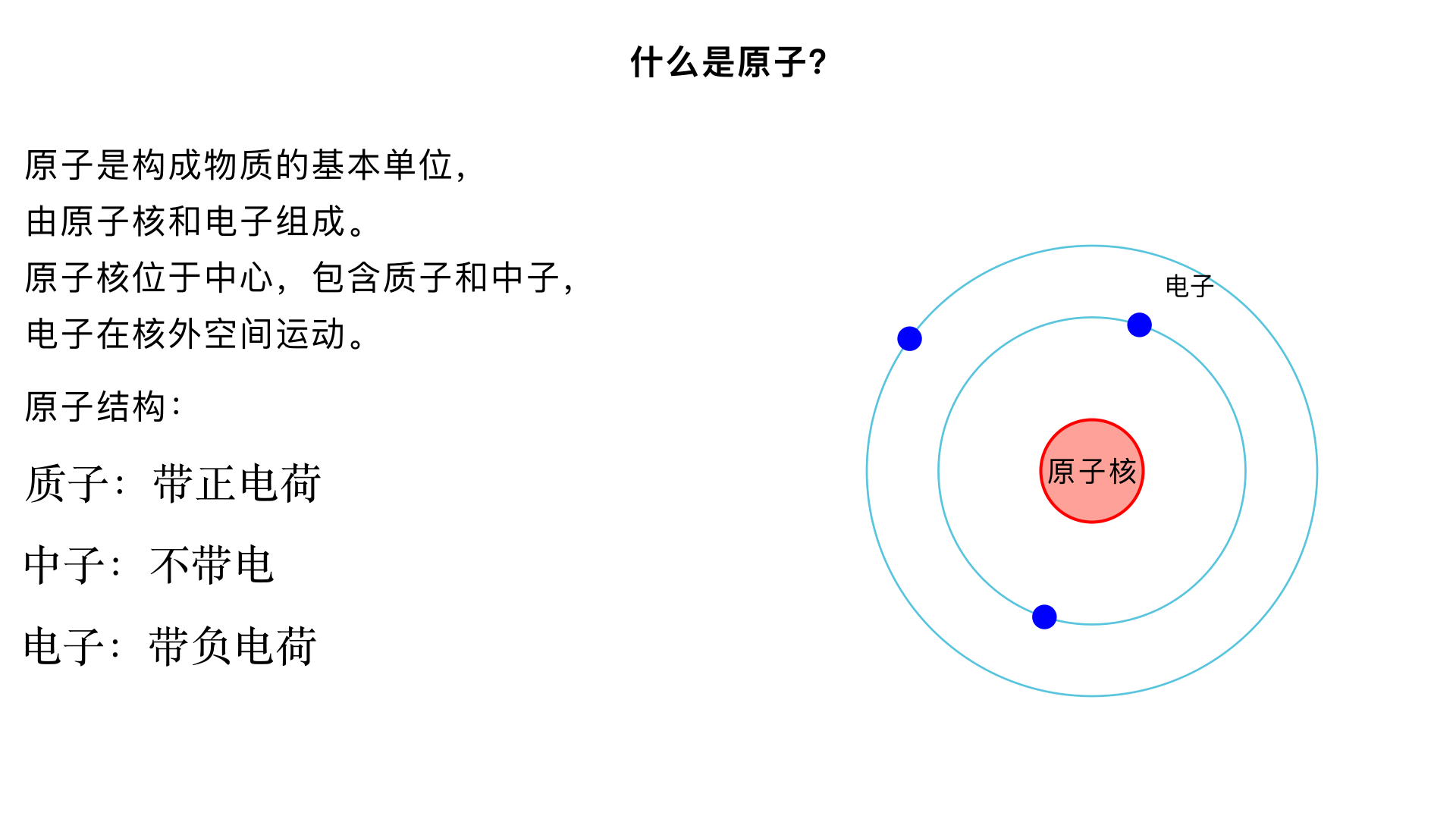
什么是原子?

▶
八年级数学 / 轴对称 / 图形的轴对称 一、核心概念(关键定义) 1. 轴对称图形 定义:如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴,折叠后重合的点是对称点(对应点)。 要点: 研究对象是一个图形的自身对称关系 对称轴是直线,不是线段或射线 一个轴对称图形的对称轴可能有一条或多条 2. 两个图形成轴对称 定义:把一个平面图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称,这条直线叫做对称轴,折叠后重合的点是对称点(对应点)。 要点: 研究对象是两个图形之间的对称关系 这两个图形是全等图形 对应点所连线段被对称轴垂直平分 3. 两者区别与联系 项目 轴对称图形 两个图形成轴对称 图形个数 1 个 2 个 对称关系 自身对称 两个图形之间对称 对称轴 1 条或多条 1 条 联系 都沿直线折叠后重合;对称轴都是对应点连线的垂直平分线;把成轴对称的两个图形看成一个整体,就是轴对称图形 二、轴对称的性质(核心定理) 全等性:成轴对称的两个图形是全等图形,对应边相等,对应角相等。 垂直平分线性质:对称轴是任何一对对应点所连线段的垂直平分线(核心性质)。 对应关系: 对应线段相等,对应线段所在直线的交点在对称轴上(或平行于对称轴) 对应角相等,对应角的两边关于对称轴对称 对称性:轴对称变换不改变图形的形状和大小,只改变图形的位置。 三、常见轴对称图形及对称轴数量 图形 对称轴数量 对称轴描述 线段 2 条 线段的垂直平分线;线段所在的直线 角 1 条 角平分线所在的直线 等腰三角形 1 条 顶角平分线(底边上的高、底边上的中线)所在直线 等边三角形 3 条 每条边上的高(中线、所对角的平分线)所在直线 矩形 2 条 对边中点连线所在直线 菱形 2 条 对角线所在直线 正方形 4 条 对边中点连线 + 两条对角线所在直线 圆 无数条 过圆心的任意直线 正 n 边形 n 条 每条边的垂直平分线(或每个内角的平分线)所在直线 四、对称轴的画法(操作步骤) 找对称点:在图形上选取若干个关键点(顶点、端点等) 作垂线:过每个关键点作对称轴的垂线 量距离:在垂线上截取与该点到对称轴距离相等的线段 连对称点:依次连接所有对称点,得到对称图形 五、轴对称的判定(识别方法) 定义法:沿某条直线折叠后,直线两旁部分完全重合 性质法: 若两个图形的对应点连线都被同一条直线垂直平分,则这两个图形成轴对称 若一个图形的所有点关于某条直线的对称点都在该图形上,则该图形是轴对称图形 六、典型例题与应用 例题 1:基础识别 下列图形中,是轴对称图形的有( )① 等腰三角形 ② 平行四边形 ③ 矩形 ④ 梯形 ⑤ 圆答案:①③⑤(解析:平行四边形无对称轴,一般梯形无对称轴) 例题 2:性质应用 已知△ABC 与△A'B'C' 关于直线 l 对称,AB=5cm,∠A=60°,则 A'B'=,∠A'=答案:5cm,60°(解析:成轴对称的图形对应边相等,对应角相等) 例题 3:作图题 已知线段 AB 和直线 l,画出线段 AB 关于直线 l 的对称线段 A'B'步骤: 过 A 作 l 的垂线,垂足为 O,延长 AO 到 A',使 OA'=OA 过 B 作 l 的垂线,垂足为 P,延长 BP 到 B',使 PB'=PB 连接 A'B',即为所求对称线段 七、易错点与注意事项 对称轴类型:对称轴是直线,不是线段或射线(如角的对称轴是角平分线所在直线,不是角平分线本身) 线段对称轴:线段有两条对称轴,不要漏掉线段所在直线 等腰三角形:对称轴是顶角平分线所在直线,也是底边上的高和中线所在直线(三线合一) 区分概念:不要混淆 “轴对称图形” 和 “两个图形成轴对称” 的概念 八、知识拓展 轴对称变换:由一个图形得到它的轴对称图形的过程叫做轴对称变换,属于全等变换 最短路径问题:利用轴对称性质解决(如 “将军饮马” 问题) 对称美:轴对称图形在建筑、艺术、设计等领域有广泛应用(如故宫、天坛等建筑) 核心口诀:轴对称,很重要,折叠重合是关键。一个图形叫对称,两个图形成轴对称。对称轴是垂直平分线,对应边等角不变。
▶
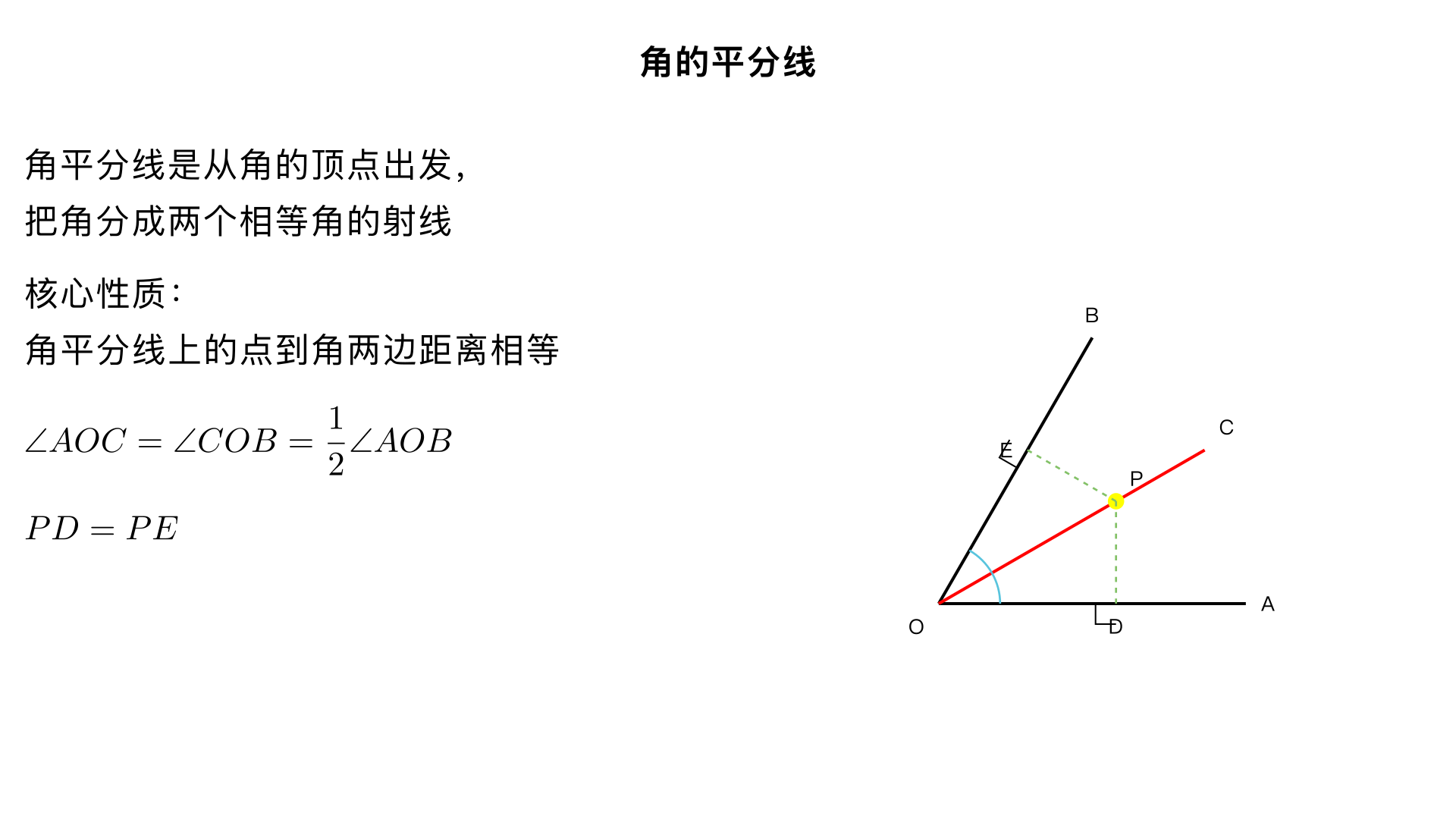
八年级数学 / 全等三角形 / 角的平分线 一、角平分线的定义与尺规作图 1. 定义 从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线。 几何表示:若 OC 是∠AOB 的平分线,则∠AOC = ∠COB = ½∠AOB 2. 尺规作图(核心技能) 已知:∠AOB求作:∠AOB 的平分线作法: 以点 O 为圆心,适当长为半径画弧,交 OA 于 M,交 OB 于 N 分别以 M、N 为圆心,大于 ½MN的长为半径画弧,两弧在∠AOB 内部交于点 P 画射线 OP,OP 即为∠AOB 的平分线 原理:SSS 全等判定(△OMP ≌ △ONP),对应角相等,故 OP 平分∠AOB 二、角平分线的核心定理(性质 + 判定) 1. 性质定理(重点) 角平分线上的点到角两边的距离相等 条件 结论 几何表示 ① 点 P 在∠AOB 的平分线上 ② PD⊥OA,PE⊥OB PD = PE ∵ OP 平分∠AOB PD⊥OA,PE⊥OB ∴ PD = PE 证明:用 AAS 判定△OPD ≌ △OPE,对应边 PD = PE 2. 判定定理(性质的逆定理) 角的内部到角两边距离相等的点,在这个角的平分线上 条件 结论 几何表示 ① 点 P 在∠AOB 内部 ② PD⊥OA,PE⊥OB ③ PD = PE 点 P 在∠AOB 的平分线上 ∵ PD⊥OA,PE⊥OB,PD = PE ∴ 点 P 在∠AOB 的平分线上 证明:用 HL 判定 Rt△OPD ≌ Rt△OPE,对应角∠AOP = ∠BOP 3. 重要推论 角的平分线是到角两边距离相等的所有点的集合 三、三角形的角平分线 1. 定义 三角形一个内角的平分线与对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线 2. 核心性质(必记) 三角形的三条角平分线相交于一点,这一点叫做三角形的内心 内心到三角形三边的距离相等(内心性质) 内心一定在三角形内部 证明:利用角平分线判定定理,证明三条角平分线交于同一点,该点到三边距离相等 四、角平分线常用辅助线(解题关键) 辅助线类型 作法 适用场景 原理 向两边作垂线 过角平分线上一点作两边的垂线段 证明线段相等、角相等 角平分线性质,构造全等直角三角形(AAS/HL) 截取构全等 在角两边截取相等线段,连接角平分线上点 证明线段和差、角相等 SAS 全等判定,构造对称全等三角形 作角平分线的垂线 延长垂线与角另一边相交 证明线段相等、构造等腰三角形 等腰三角形三线合一,构造对称图形 角平分线 + 平行线 过角一边上点作角平分线的平行线 构造等腰三角形 等角对等边,平行线性质 口诀:图中有角平分线,可向两边作垂线;也可将图对折看,对称以后关系现;角平分线平行线,等腰三角形来添;角平分线加垂线,三线合一试试看 五、典型例题与解法(全等三角形应用) 例 1:性质定理应用 已知:在△ABC 中,∠C = 90°,AD 平分∠BAC,DE⊥AB 于 E,AC = 6,BC = 8求:CD 的长 解法: ∵ AD 平分∠BAC,DC⊥AC,DE⊥AB ∴ CD = DE(角平分线性质) 设 CD = x,则 DE = x,DB = 8 - x 易证 Rt△ACD ≌ Rt△AED(HL),故 AE = AC = 6 AB = √(AC² + BC²) = 10,BE = AB - AE = 4 在 Rt△BDE 中,x² + 4² = (8 - x)²,解得 x = 3 答案:CD = 3 例 2:判定定理应用 已知:在四边形 ABCD 中,∠B = ∠D = 90°,点 E 在 BC 上,且 AE 平分∠BAD,CE = DE求证:BE = DE 证明: 过 E 作 EF⊥AD 于 F ∵ AE 平分∠BAD,∠B = 90°,EF⊥AD ∴ BE = EF(角平分线性质) ∵ ∠D = 90°,CE = DE,且 CE⊥CD,DE⊥CD ∴ 点 E 在∠ADC 的平分线上(角平分线判定) 又 EF⊥AD,DE⊥CD,故 EF = DE ∴ BE = DE(等量代换) 例 3:辅助线构造(截取法) 已知:AD 平分∠BAC,AB > AC,求证:AB - AC = BD - DC 证明: 在 AB 上截取 AE = AC(构造全等) ∵ AD 平分∠BAC,故∠EAD = ∠CAD 在△AED 和△ACD 中: AE = AC,∠EAD = ∠CAD,AD = AD ∴ △AED ≌ △ACD(SAS),故 DE = DC AB - AC = AB - AE = BE BD - DC = BD - DE 在△BDE 中,BE = BD - DE(线段和差) ∴ AB - AC = BD - DC 六、易错点与注意事项 性质定理的两个必要条件: 点在角平分线上 到角两边的距离(必须是垂线段) 易错:忽略垂直关系,直接说 "角平分线上的点到角两边的线段相等" 判定定理的前提: 点必须在角的内部(外部点不适用) 三角形角平分线与角平分线区别: 前者是线段,后者是射线 内心与外心区别: 内心:三条角平分线交点,到三边距离相等 外心:三边垂直平分线交点,到三个顶点距离相等 七、思维导图(核心知识框架) plaintext 角的平分线 ├── 定义:分角为两等份的射线 ├── 尺规作图:三步骤+SSS原理 ├── 两大定理 │ ├── 性质:角平分线上点→到两边距离相等 │ └── 判定:到两边距离相等点→在角平分线上 ├── 三角形角平分线 │ ├── 定义:内角平分线与对边交点的线段 │ └── 性质:三线共点(内心),到三边等距 └── 辅助线技巧 ├── 向两边作垂线 ├── 截取构全等 ├── 作角平分线垂线 └── 角平分线+平行线 八、巩固练习(基础 + 提升) 基础题 如图,OP 平分∠AOB,PC⊥OA 于 C,PD⊥OB 于 D,PC = 3,则 PD = ____(答案:3) 三角形的三条角平分线相交于一点,这个点叫做三角形的____(答案:内心) 提升题 已知:在△ABC 中,∠B = 60°,∠C = 40°,AD 平分∠BAC,求∠ADC 的度数(答案:100°) 如图,∠B = ∠C = 90°,M 是 BC 中点,DM 平分∠ADC,求证:AM 平分∠DAB(提示:作 MN⊥AD 于 N)
▶