T
Teach Me AnythingTMA
Video History
Page 24 / 43
▶
主题17、爱的发现 (哈洛的“恒河猴依恋”实验) 主要内容:让小猴子在“铁丝母猴”和“绒布母猴”之间选择,尽管只有铁丝母猴提供食物,小猴子仍绝大部分时间依偎在绒布母猴身边。这项研究颠覆了“有奶便是娘”的观点,证明了接触舒适感是形成依恋的关键,比喂食更重要。

▶
第十七课、爱的发现 (哈洛的“恒河猴依恋”实验) 主要内容:让小猴子在“铁丝母猴”和“绒布母猴”之间选择,尽管只有铁丝母猴提供食物,小猴子仍绝大部分时间依偎在绒布母猴身边。这项研究颠覆了“有奶便是娘”的观点,证明了接触舒适感是形成依恋的关键,比喂食更重要。
▶
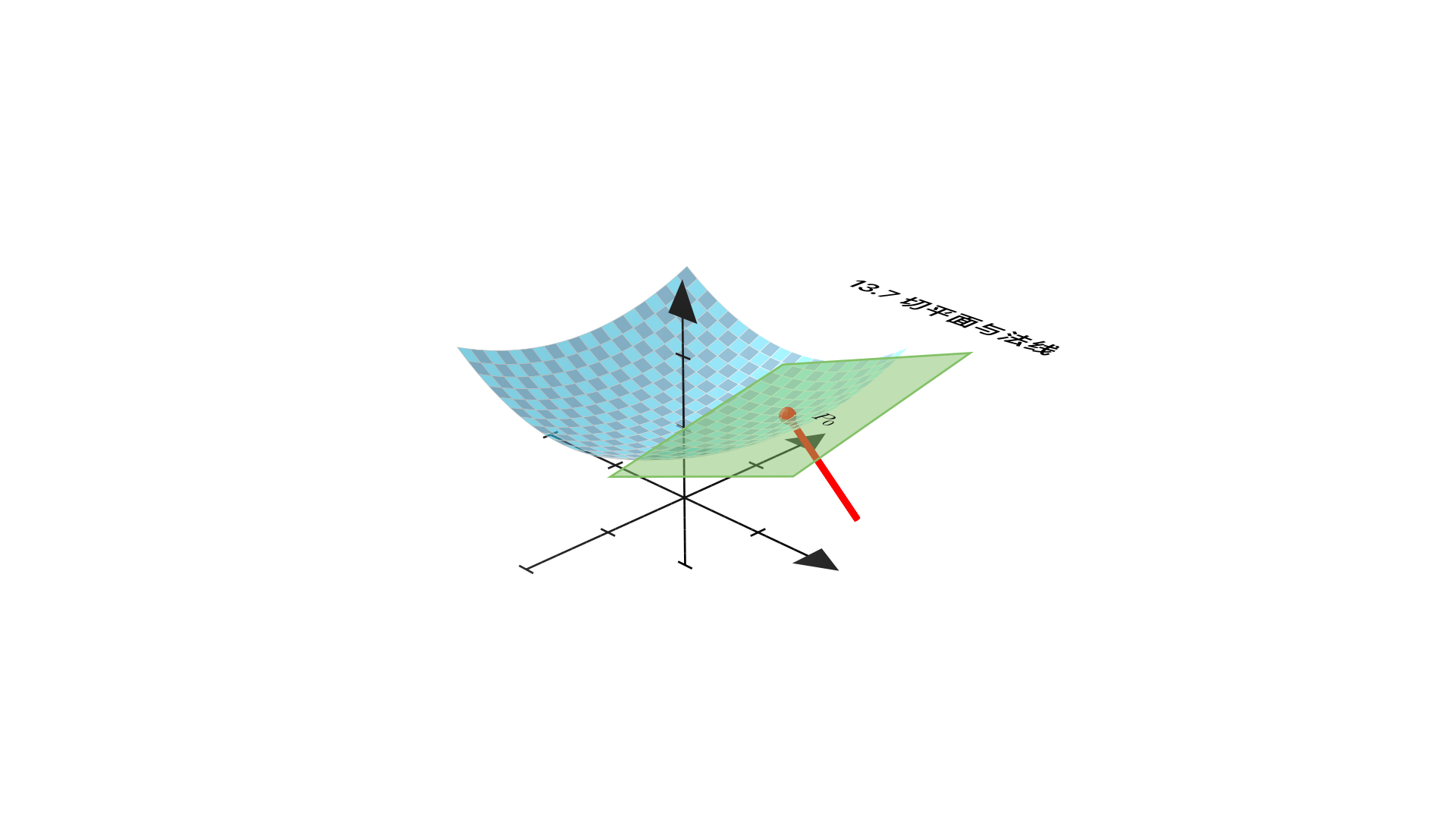
第13 章 多元函数 第 13.7 节 切平面与法线

▶
爱的发现 (哈洛的“恒河猴依恋”实验) 主要内容:让小猴子在“铁丝母猴”和“绒布母猴”之间选择,尽管只有铁丝母猴提供食物,小猴子仍绝大部分时间依偎在绒布母猴身边。这项研究颠覆了“有奶便是娘”的观点,证明了接触舒适感是形成依恋的关键,比喂食更重要。
▶
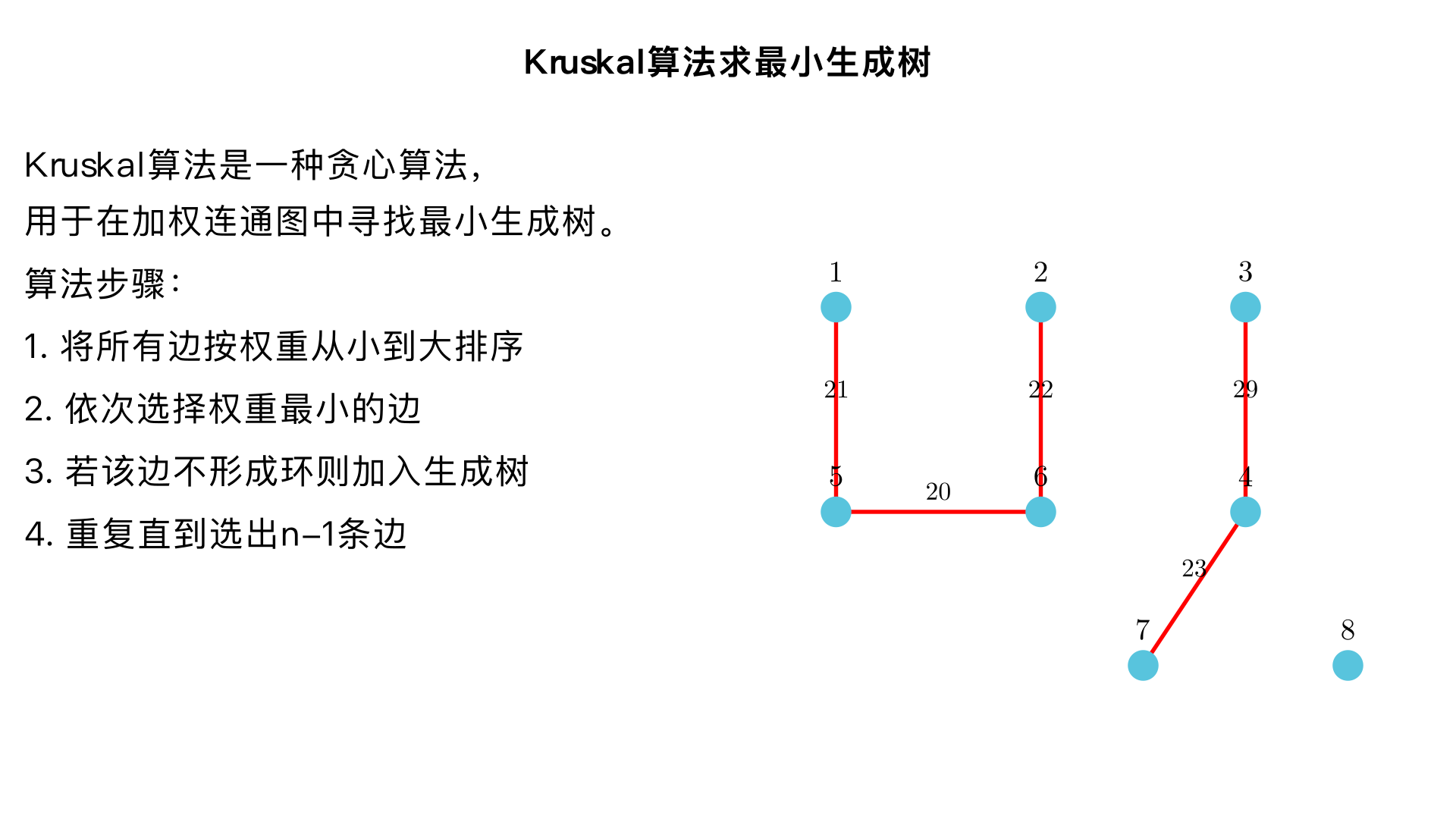
# **Section 3** ## **题目 2** 使用 Kruskal 算法为下面的图找到一棵最小生成树。 除了得到最小生成树外,还要给出算法过程中最终形成的根树。 在合并两棵树时,以编号较小的顶点作为新树的根。 Figure 16.3.13. Graph 2(a) ``` 1: (2,41), (5,21) 2: (1,41), (3,32), (5,42), (6,22) 3: (2,32), (4,29), (7,31) 4: (3,29), (7,23), (8,44) 5: (1,21), (2,42), (6,20) 6: (5,20), (2,22), (7,62) 7: (6,62), (3,31), (4,23), (8,45) 8: (7,45), (4,44) ``` Figure 16.3.14. Graph 2(b) ```text 1: (2, 10), (4, 7), (8, 10) 2: (1, 10), (3, 11), (5, 14), (7, 10) 3: (2, 11), (4, 12), (6, 16), (8, 8) 4: (1, 7), (3, 12), (5, 13), (7, 15) 5: (2, 14), (4, 13), (6, 13), (8, 9) 6: (1, 7), (3, 16), (5, 13), (7, 12) 7: (2, 10), (4, 15), (6, 12), (8, 11) ```
▶
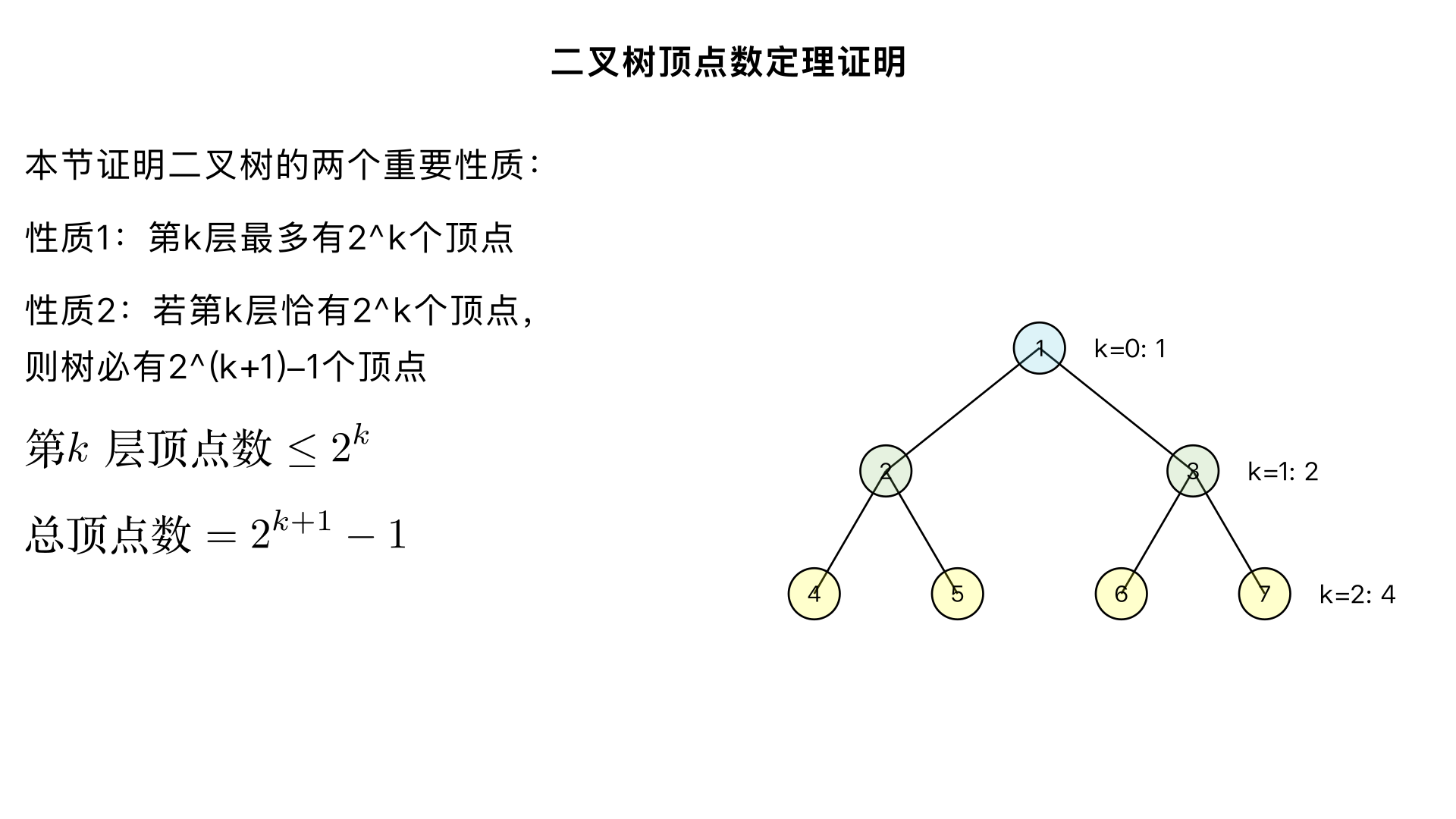
## **题目 6** 证明:二叉树中第 ( k ) 层最多有 ( 2^k ) 个顶点;并且若某棵树在第 ( k ) 层恰有 ( 2^k ) 个顶点,则它必须有 ( 2^{k+1} - 1 ) 个顶点。
▶
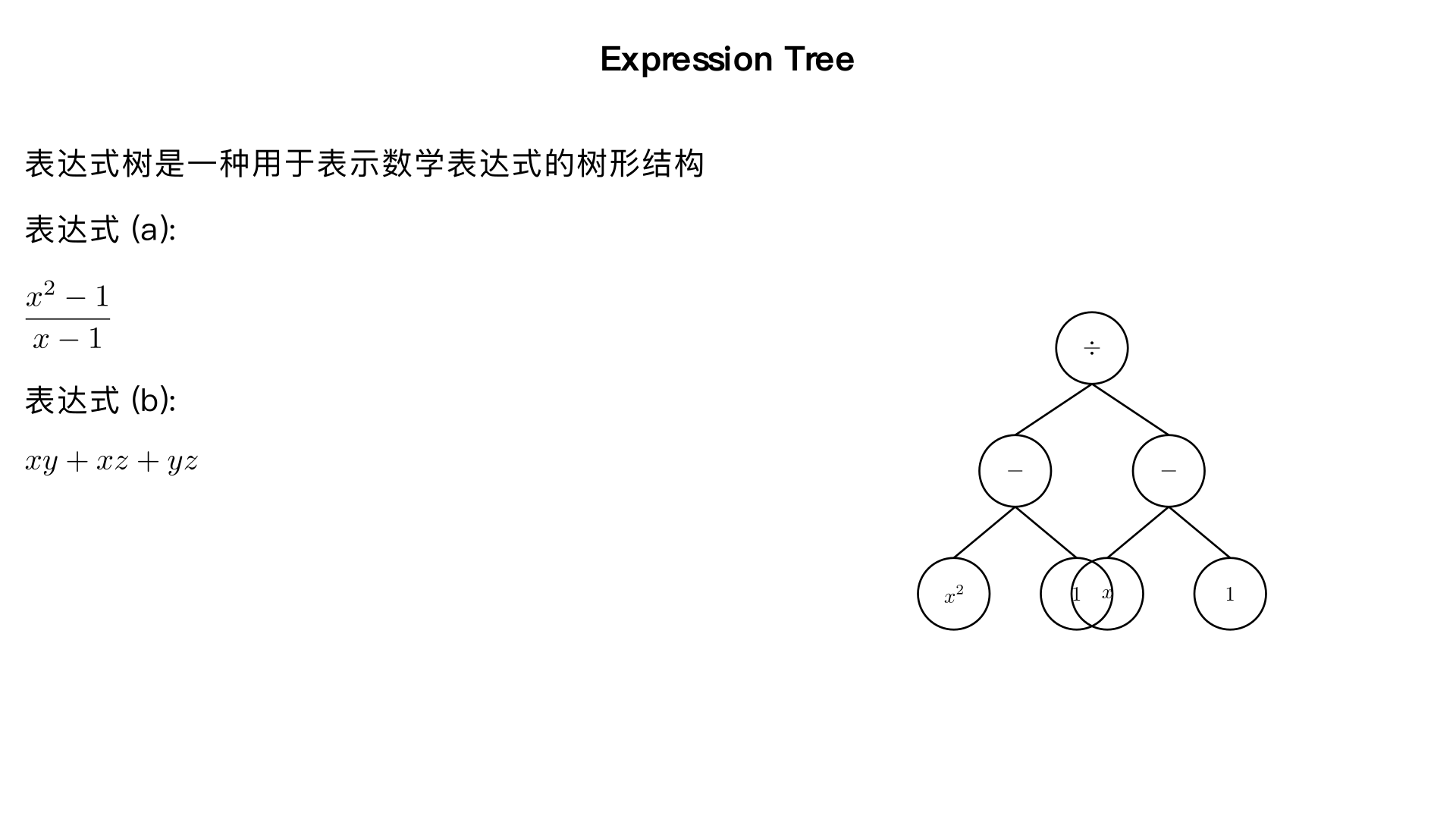
## **题目 2** 为以下表达式画出表达式树: (a) (\dfrac{x^2 - 1}{x - 1}) (b) (xy + xz + yz)
▶
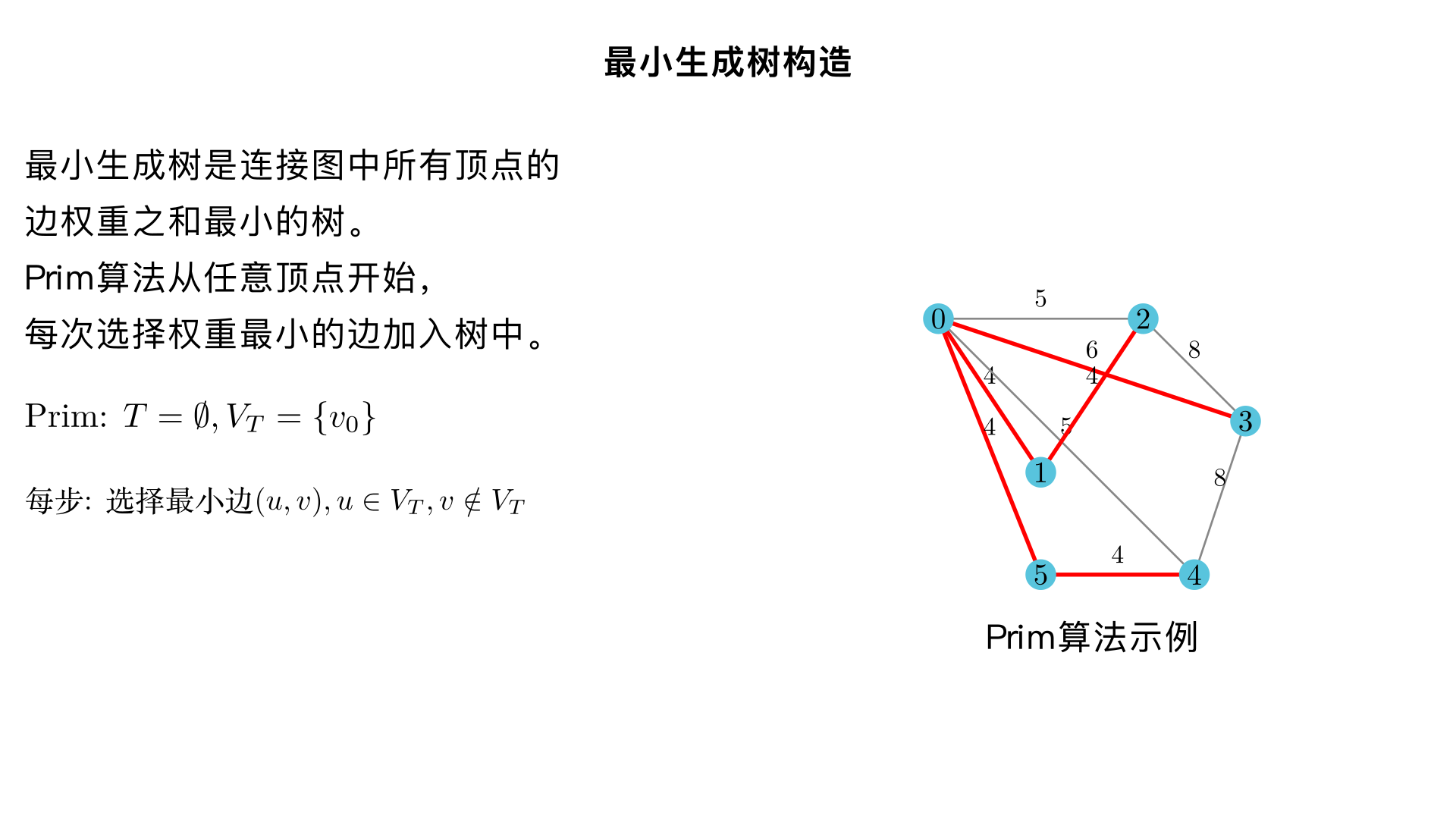
为以下图形构造一棵最小生成树。 (包含图 (a)、(b)、(c)) # **(a) 图的邻接表** 节点:0, 1, 2, 3, 4, 5 ``` 0: (1,4), (2,5), (3,6), (4,5), (5,4) 1: (0,4), (2,4) 2: (1,4), (0,5), (3,8) 3: (2,8), (0,6), (4,8) 4: (3,8), (0,5), (5,4) 5: (4,4), (0,4) ``` --- # **(b) 图的邻接表** 城市节点:SF, LA, CHI, KC, BOS, NY, PHI, DC, ATL 根据图中边和权重整理如下: ``` SF: (LA,50), (CHI,100) LA: (SF,50), (CHI,120), (KC,90) CHI: (SF,100), (LA,120), (KC,40), (PHI,80), (NY,90), (BOS,90) KC: (LA,90), (CHI,40), (PHI,70), (ATL,80) BOS: (CHI,90), (NY,40) NY: (BOS,40), (CHI,90), (PHI,30), (DC,30) PHI: (CHI,80), (KC,70), (NY,30), (DC,35) DC: (NY,30), (PHI,35), (ATL,60) ATL: (KC,80), (DC,60) ``` --- # **(c) 图的邻接表** 节点:1,3,4,5,6,7,8 ``` 1: (2,6), (4,10), (8,2) 2: (1,6), (3,4), (7,4) 3: (2,4), (4,6), (6,2), (7,3) 4: (1,10), (3,6), (5,2) 5: (4,2), (6,6), (8,11) 6: (3,2), (5,6), (7,4) 7: (2,4), (3,3), (6,4), (8,6) 8: (1,2), (7,6), (5,11) ``` 要求:必须使用 Prim 算法,并展示加入顶点和边的顺序。
▶
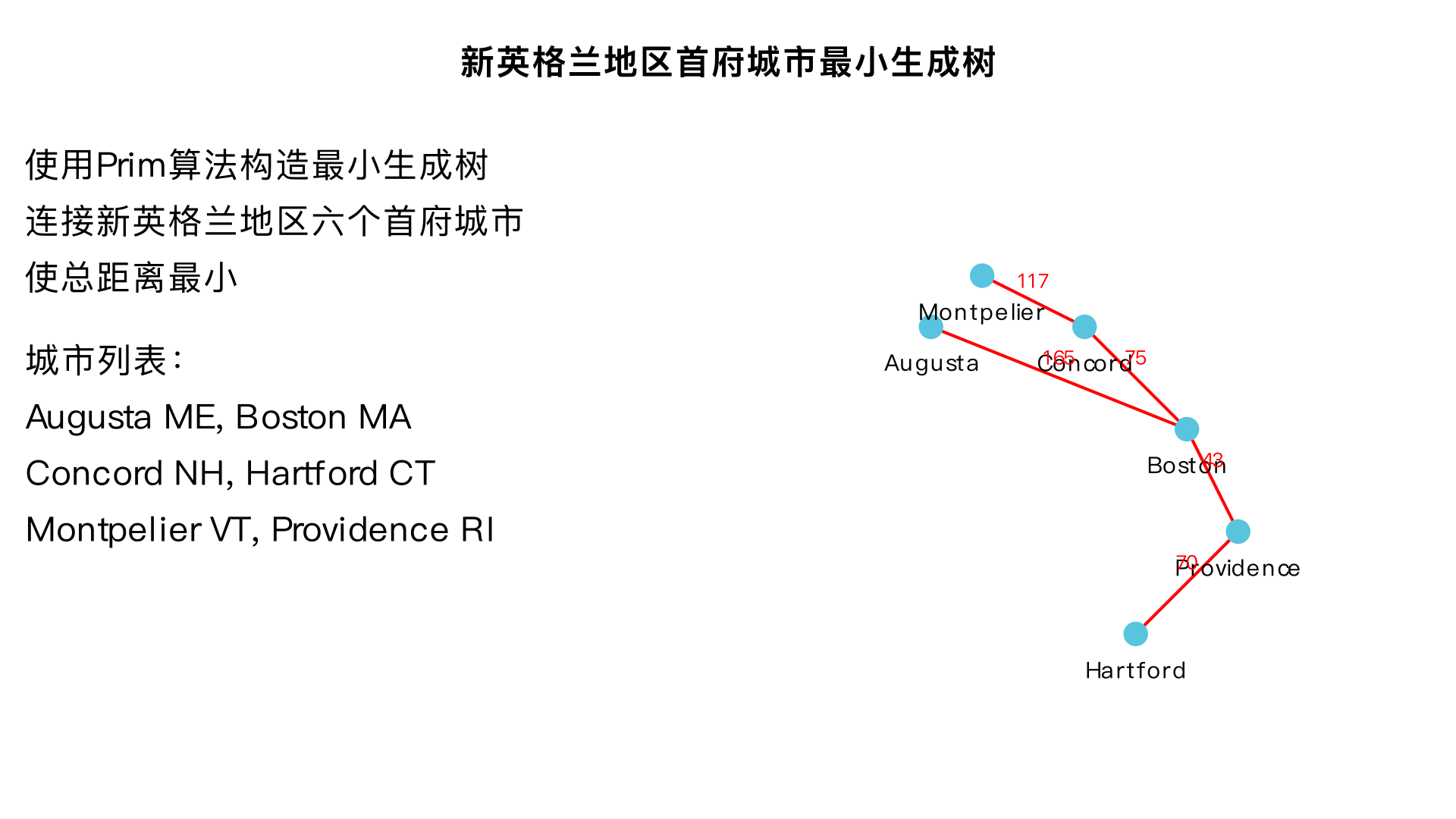
利用美国新英格兰地区各首府城市之间的距离表,构造一棵最小生成树。 Table 15.5.3. Distances between capital cities in New England | | Augusta | Boston | Concord | Hartford | Montpelier | Providence | |----------------|---------|--------|---------|----------|------------|------------| | Augusta, ME | -- | 165 | 148 | 266 | 190 | 208 | | Boston, MA | 165 | -- | 75 | 103 | 192 | 43 | | Concord, NH | 148 | 75 | -- | 142 | 117 | 109 | | Hartford, CT | 266 | 103 | 142 | -- | 204 | 70 | | Montpelier, VT | 190 | 192 | 117 | 204 | -- | 223 | | Providence, RI | 208 | 43 | 109 | 70 | 223 | -- | 要求:必须使用 Prim 算法,并展示加入顶点和边的顺序。
▶
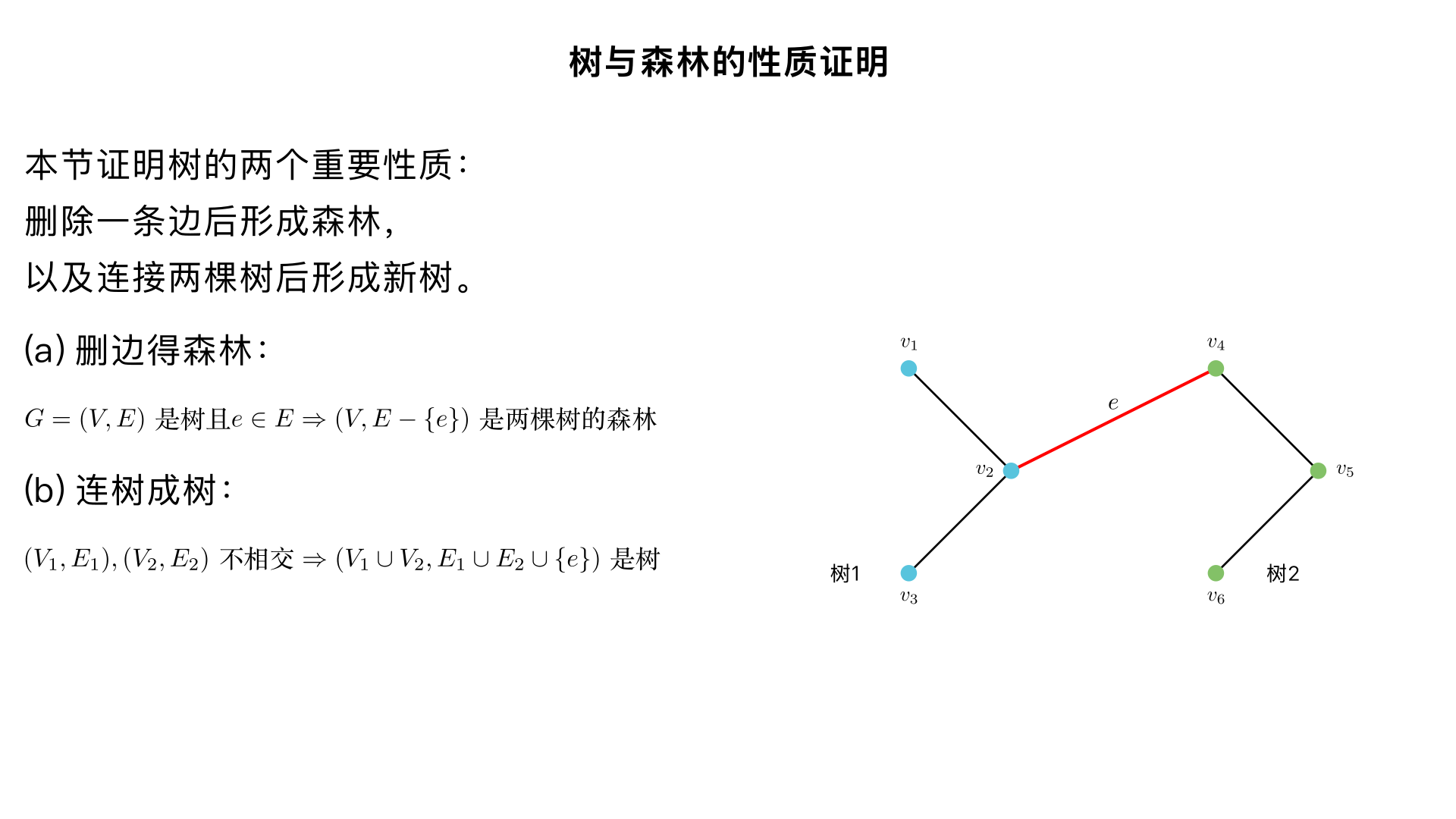
(a) 证明:如果 ( G = (V, E) ) 是一棵树且 ( e \in E ),那么 ( (V, E - {e}) ) 是由两棵树组成的森林。 (b) 证明:如果 ( (V_1, E_1) ) 和 ( (V_2, E_2) ) 是不相交的两棵树,并且 ( e ) 是一条连接 ( V_1 ) 中某个顶点与 ( V_2 ) 中某个顶点的边,那么 ( (V_1 \cup V_2, E_1 \cup E_2 \cup {e}) ) 是一棵树。
▶
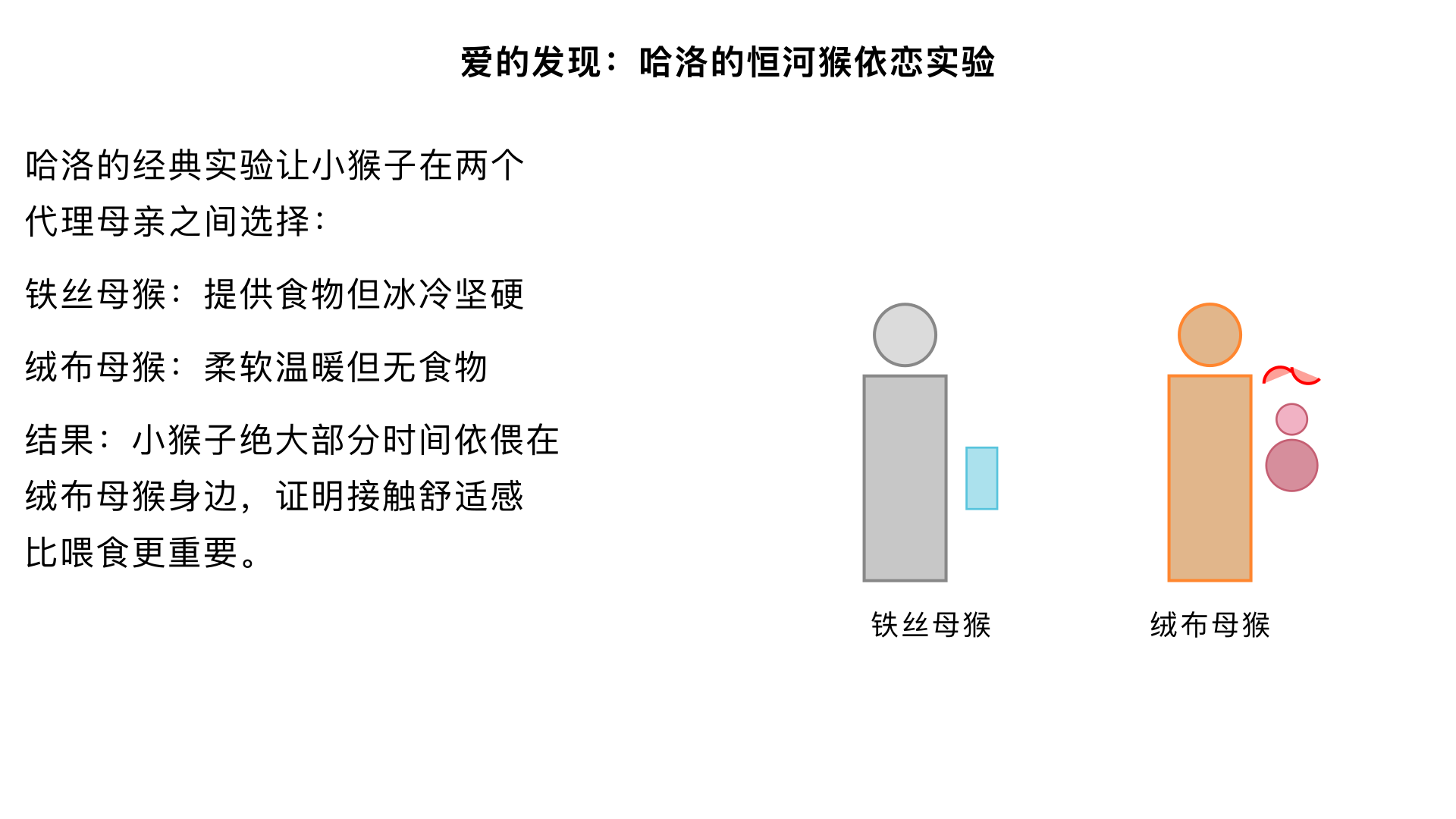
17、爱的发现 (哈洛的“恒河猴依恋”实验) 主要内容:让小猴子在“铁丝母猴”和“绒布母猴”之间选择,尽管只有铁丝母猴提供食物,小猴子仍绝大部分时间依偎在绒布母猴身边。这项研究颠覆了“有奶便是娘”的观点,证明了接触舒适感是形成依恋的关键,比喂食更重要。

▶