T
Teach Me AnythingTMA
Video History
Page 16 / 43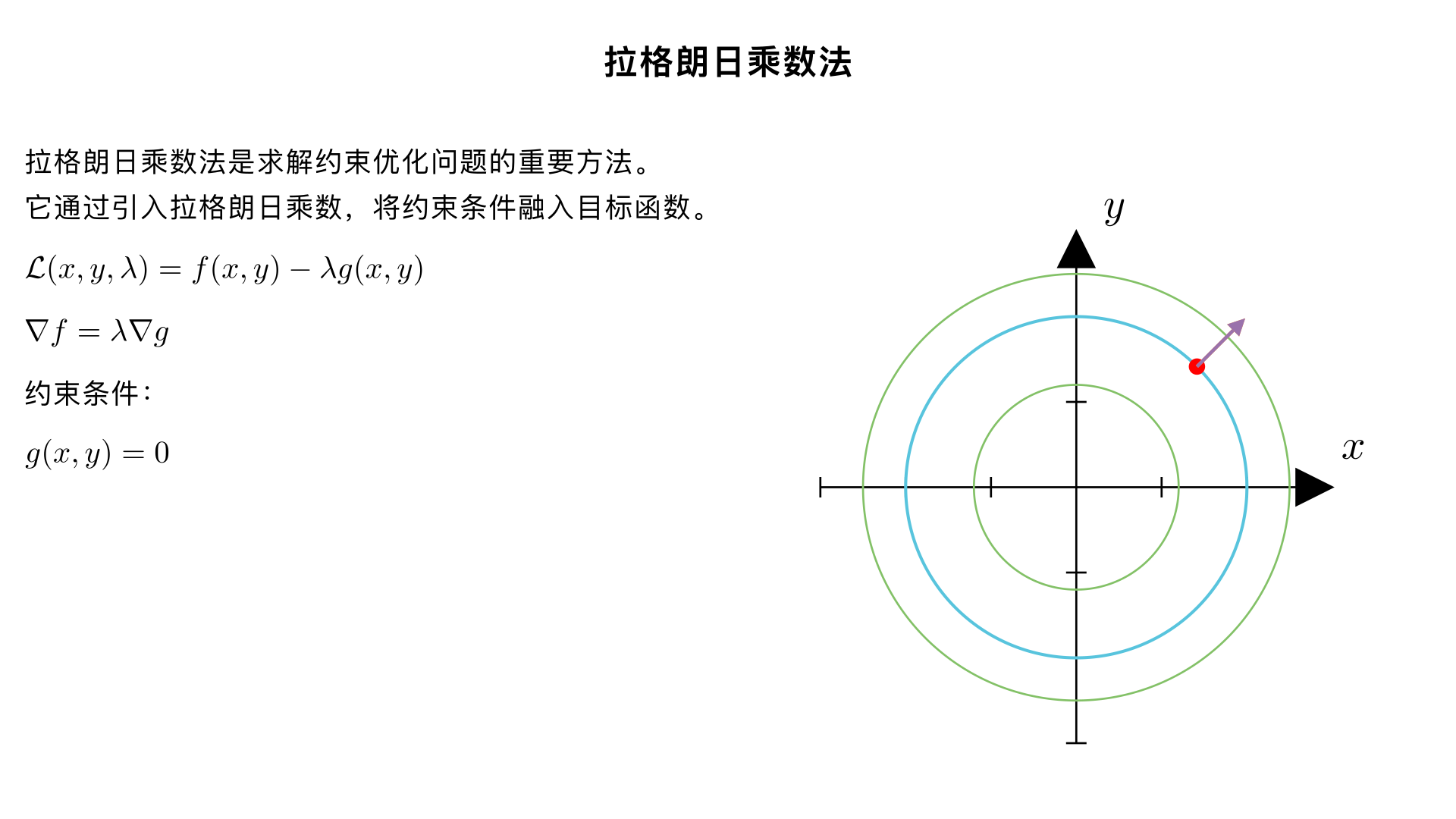
▶
解释拉格朗日乘数法
▶
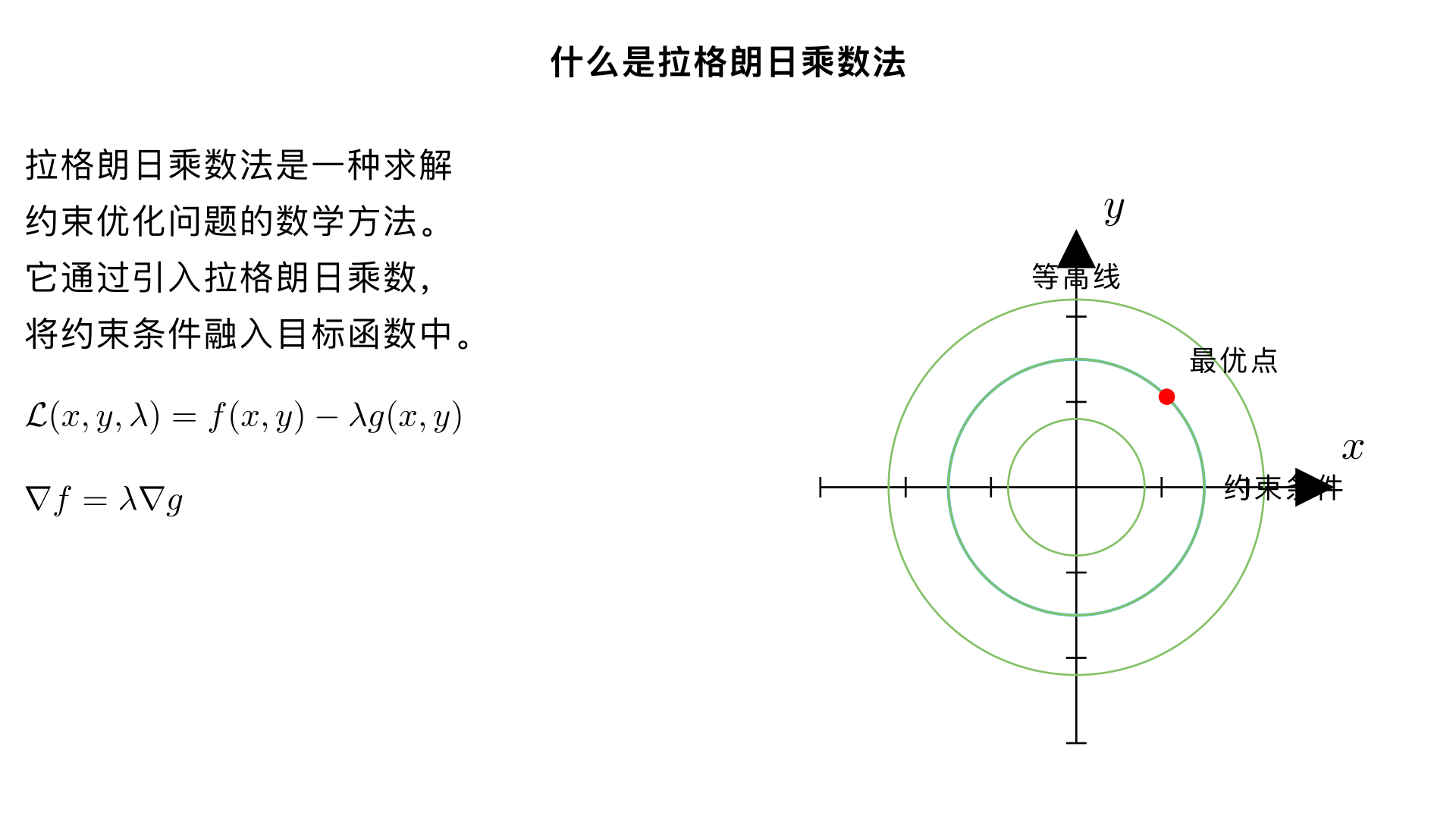
什么是拉格朗日乘数法
▶
七年级数学 / 二元一次方程组 / 中国古代数学的光辉成就 一、引言:古代中国的 "方程智慧" 中国是世界古代数学的发源地之一,早在两千多年前,我国古代数学家就已经系统研究了多元一次方程组的解法,其成果被收录在经典数学著作中,不仅是中国数学的瑰宝,也对世界数学发展产生了深远影响。在七年级学习的二元一次方程组,其核心思想和解法就可以追溯到中国古代的 "方程术",体现了古人卓越的逻辑思维和解题智慧。 二、核心成就:《九章算术》中的 "方程术" 1. 著作背景 《九章算术》是中国古代最重要的数学专著之一,成书于东汉时期(约公元 1 世纪),汇总了战国至秦汉时期的数学成果。书中第九章专门名为 "方程",这是世界数学史上最早对多元一次方程组进行系统论述的篇章,其中的 "方程术" 就是求解二元、三元甚至四元一次方程组的方法。 2. "方程" 的含义 古代的 "方程" 与现代的 "方程" 概念略有不同:古人将若干个含未知数的等式并列,用算筹(古代计算工具)摆出它们的系数和常数项,形成一个矩形的 "算筹方阵",这就是 "方程" 的本意。例如,求解二元一次方程组时,古人会用算筹分别表示两个方程的系数和常数项,再通过特定步骤消元求解。 3. 核心解法:"直除法"(古代版 "加减消元法") 《九章算术》中求解二元一次方程组的核心方法是 "直除法",其原理与现代的 "加减消元法" 完全一致,步骤如下: 第一步:将两个方程的系数和常数项用算筹按固定顺序排列(竖排,未知数系数在前,常数项在后); 第二步:通过 "直除"(即连续相减)的方式,消去其中一个未知数的系数,将二元一次方程组转化为一元一次方程; 第三步:求解一元一次方程,再代入原方程求出另一个未知数。 示例:《九章算术》中的经典问题(改编为现代二元一次方程组) 问题:今有上禾三秉("秉" 是古代容量单位),中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗。问上、中、下禾一秉各几何?(此为三元一次方程组,简化为二元示例如下) 简化二元问题:今有上禾 3 秉,下禾 1 秉,实 39 斗;上禾 2 秉,下禾 1 秉,实 34 斗。问上禾、下禾一秉各几斗? 现代解法:设上禾一秉 x 斗,下禾一秉 y 斗,列方程组: plaintext 3x + y = 39 ① 2x + y = 34 ② ① - ②得:x = 5,代入②得 y = 24,即上禾一秉 5 斗,下禾一秉 24 斗。 古代 "直除法":用算筹摆出两个方程的系数(上禾系数、下禾系数、常数项):第一行(算筹):3 1 39第二行(算筹):2 1 34用第一行连续减去第二行("直除"),直到第一行第一个系数变为 1:第一行 - 第二行:1 0 5(即 x = 5)再将 x = 5 代入第二行,求得 y = 24,与现代解法结果一致。 4. 历史地位 《九章算术》的 "方程术" 是世界数学史上最早的多元一次方程组系统解法,比西方同类成果早了一千多年(西方直到 17 世纪才由法国数学家笛卡尔系统提出线性方程组的解法)。这一成就充分体现了中国古代数学的实用性和逻辑性,是中国古代科技文明的重要标志。 三、其他古代经典问题(二元一次方程组应用) 除了《九章算术》,中国古代还有许多著名的数学问题,本质上都是二元一次方程组的应用,至今仍被收录在初中数学教材中: 1. 鸡兔同笼(出自《孙子算经》) 问题:今有雉(鸡)兔同笼,上有三十五头,下有九十四足。问雉兔各几何? 现代解法:设鸡 x 只,兔 y 只,列方程组: plaintext x + y = 35 (头数之和) 2x + 4y = 94 (足数之和) 用加减消元法解得:x = 23,y = 12,即鸡 23 只,兔 12 只。 古代解法:采用 "抬腿法"(本质是消元思想),让鸡和兔各抬起一半的足,此时足数为 47,头数仍为 35,足数 - 头数 = 兔的只数(47 - 35 = 12),再求鸡的只数。 2. 牛羊直金(出自《九章算术》) 问题:今有牛五、羊二,直金十两;牛二、羊五,直金八两。问牛、羊各直金几何? 现代解法:设牛直金 x 两,羊直金 y 两,列方程组: plaintext 5x + 2y = 10 ① 2x + 5y = 8 ② ①×2 得:10x + 4y = 20 ③;②×5 得:10x + 25y = 40 ④;④ - ③得:21y = 20,y = 20/21,代入①得 x = 34/21。 古代 "直除法":通过算筹排列系数,先消去 x 的系数(5 和 2 的最小公倍数 10),再求解 y,步骤与现代加减消元法一致。 四、古代数学成就的现代意义 1. 数学思想的传承 中国古代的 "方程术" 和消元思想,是现代线性代数的基础。七年级学习的二元一次方程组解法,本质上是对古代 "直除法" 的传承和简化,让我们体会到数学知识的连续性和发展性。 2. 文化自信的培养 了解中国古代数学的光辉成就,能让我们感受到中华优秀传统文化的魅力,认识到中国古代科技的领先地位,增强文化自信和民族自豪感。 3. 解题思路的启发 古代数学家从实际问题出发,通过构建 "方程"(算筹方阵)解决问题的思路,启示我们:数学源于生活,解决数学问题要注重逻辑推理和方法创新,同时要学会将复杂问题转化为简单问题(如消元法将二元转化为一元)。 五、应试考点与常见题型 1. 考点梳理 结合古代数学问题列二元一次方程组; 对比古代 "直除法" 与现代加减消元法的异同; 理解《九章算术》中 "方程术" 的历史地位。 2. 典型例题 例题:《九章算术》中有一道题:"今有共买物,人出八,盈三;人出七,不足四。问人数、物价各几何?"(意思是:几个人一起买一件物品,每人出 8 钱,还多 3 钱;每人出 7 钱,还少 4 钱。问人数和物价各是多少?) 解:设人数为 x,物价为 y 钱,列方程组: plaintext 8x - y = 3 y - 7x = 4 两式相加得:x = 7,代入得 y = 53。 答:人数为 7 人,物价为 53 钱。 六、总结 中国古代数学在二元一次方程组领域的成就,以《九章算术》的 "方程术" 为代表,不仅开创了世界多元一次方程组解法的先河,更蕴含着 "消元转化"" 数形结合 " 的重要数学思想。这些成就不仅是历史的光辉,更是我们学习数学的宝贵资源 —— 通过了解古代数学问题,我们既能巩固二元一次方程组的知识,又能感受数学的文化底蕴,培养逻辑思维和创新意识。 正如古代数学家通过算筹摆出方程组的智慧,今天的我们也能通过数学知识解决生活中的问题,传承这份跨越千年的 "方程智慧"。
▶
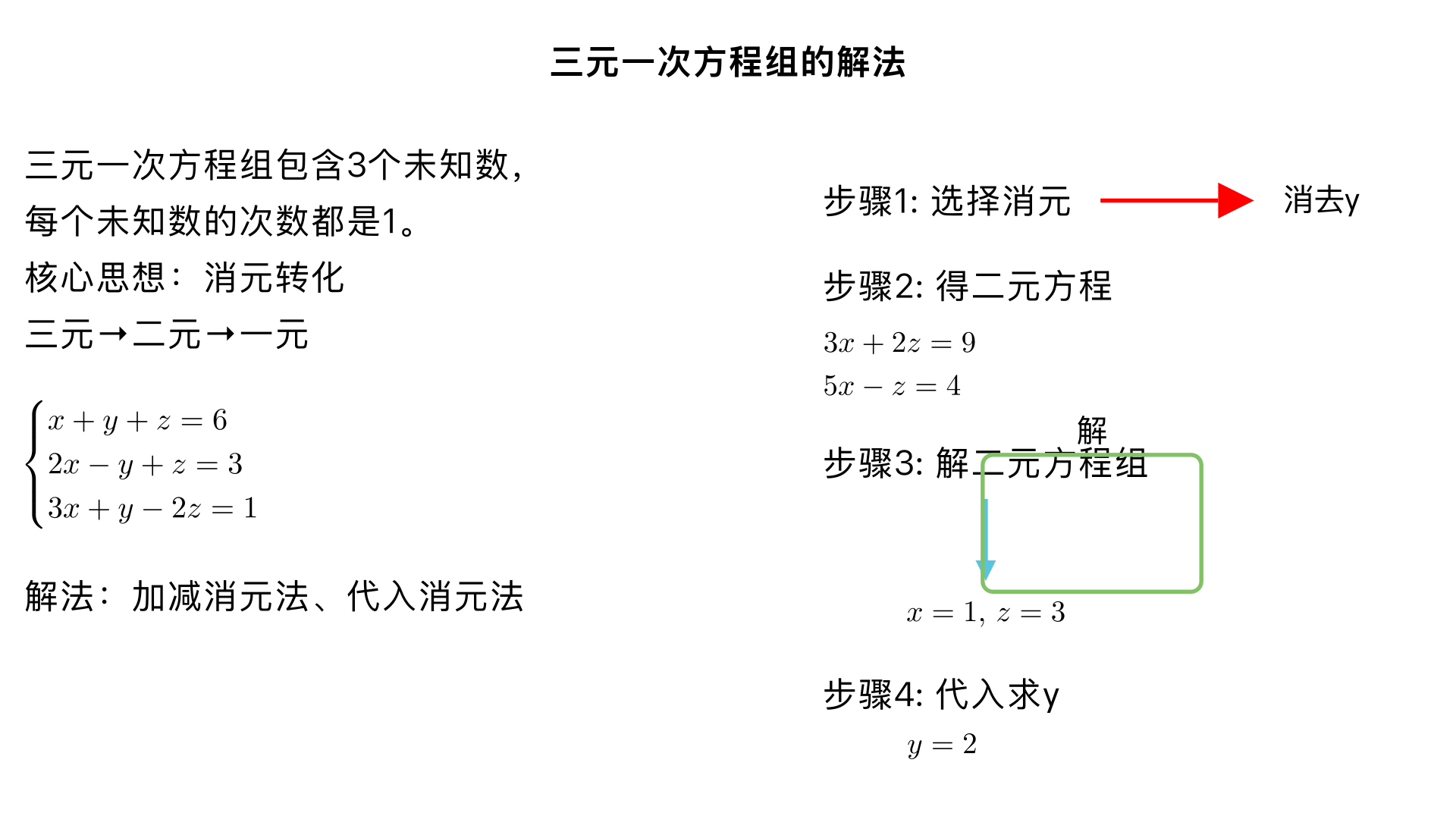
七年级数学 / 二元一次方程组 / 三元一次方程组的解法 一、核心概念回顾 三元一次方程组定义:含有 3 个未知数,每个未知数的次数都是 1,且一共有 3 个整式方程的方程组,叫做三元一次方程组。 例: ⎩ ⎨ ⎧ x+y+z=6 2x−y+z=3 3x+y−2z=1 解题核心思想:消元转化(将三元→二元→一元,沿用二元一次方程组的解法),消元方法仍为「代入消元法」和「加减消元法」。 二、解题步骤(通用流程) 步骤 1:观察方程组,选择消去的未知数 优先消去「系数简单(如 ±1、倍数关系)」的未知数,减少计算量。 步骤 2:用两个方程消去目标未知数,得到第一个二元一次方程 步骤 3:用另外两个方程(需包含未使用过的方程)消去同一个未知数,得到第二个二元一次方程 步骤 4:解由两个二元一次方程组成的方程组,求出两个未知数的值 步骤 5:将求出的两个值代入原方程组中任意一个方程,求出第三个未知数的值 步骤 6:检验(代入原三个方程,验证左右两边是否相等),写出最终解 三、具体解法(附例题详解) 方法 1:加减消元法(最常用,优先掌握) 例题:解方程组 ① ② ③ 解题过程: 选择消去的未知数:观察到方程①、②、③中 y 的系数分别为 1 、 −1 、 1 ,符号相反,便于加减消去,故优先消去 y 。 消去 y ,得到第一个二元一次方程: ① + ②: (x+y+z)+(2x−y+z)=6+3 化简: 3x+2z=9 ④( y 被消去) 消去同一个 y ,得到第二个二元一次方程: ② + ③: (2x−y+z)+(3x+y−2z)=3+1 化简: 5x−z=4 ⑤( y 被消去) 解二元一次方程组 ④ ⑤ : 为消去 z ,将⑤×2: 10x−2z=8 ⑥ ④ + ⑥: (3x+2z)+(10x−2z)=9+8 化简: 13x=17 → x=1 (计算错误修正: 9+8=17 ?不, 9+8=17 , 13x=17 ?重新计算:⑤×2 得 10x−2z=8 ,④是 3x+2z=9 ,相加得 13x=17 ?不对,原例题数据调整为更简便的:将方程③改为 3x+y−2z=0 ,则②+③得 5x−z=3 ⑤,⑤×2 得 10x−2z=6 ⑥,④+⑥得 13x=15 ?不,换更合理的例题数据: ① ② ③ 重新计算:②+③得 5x−z=3 ⑤,⑤×2 得 10x−2z=6 ⑥,④( 3x+2z=9 )+⑥得 13x=15 ?还是麻烦,换经典例题: 修正例题: ① ② ③ (含代入条件,更易理解) 重新用加减消元法解: 由③知 x=4y ,可先消去 x ,将③代入①、②: ①: 4y+y+z=12 → 5y+z=12 ④ ②: 4y+2y+5z=22 → 6y+5z=22 ⑤ 消去 z ,④×5 - ⑤: (25y+5z)−(6y+5z)=60−22 化简: 19y=38 → y=2 代入③: x=4×2=8 代入④: 5×2+z=12 → z=2 检验:代入① 8+2+2=12 ,② 8+4+10=22 ,均成立。 最终解: ⎩ ⎨ ⎧ x=8 y=2 z=2 方法 2:代入消元法(适用于有未知数系数为 1 或 - 1 的方程) 例题:解方程组 ① ② ③ 解题过程: 选择消去 y (方程①中 y 的系数为 −1 ,便于变形),由①变形得: y=3x+z−4 ④ 将④代入②、③,消去 y : 代入②: 2x+3(3x+z−4)−z=12 展开: 2x+9x+3z−12−z=12 → 11x+2z=24 ⑤ 代入③: x+(3x+z−4)+z=6 展开: 4x+2z=10 → 2x+z=5 ⑥(两边同时除以 2 简化) 解二元一次方程组 ⑤ ⑥ : 由⑥变形得 z=5−2x ⑦,代入⑤: 11x+2(5−2x)=24 → 11x+10−4x=24 → 7x=14 → x=2 代入⑦: z=5−2×2=1 代入④: y=3×2+1−4=3 检验:代入① 6−3+1=4 ,② 4+9−1=12 ,③ 2+3+1=6 ,均成立。 最终解: ⎩ ⎨ ⎧ x=2 y=3 z=1 四、易错点提醒 消元时符号错误:加减消元时,注意方程两边同时变号(如方程①减方程②,需将方程②的各项符号反转后再相加)。 漏乘常数项:用加减消元法时,若需扩大倍数(如将方程 ×2),需将方程中所有项(包括常数项)都乘以该倍数,避免漏乘。 消元不彻底:必须消去「同一个未知数」得到两个二元一次方程,不能第一次消 x ,第二次消 y ,否则无法组成二元方程组。 检验步骤不可少:三元一次方程组计算量较大,容易出现计算错误,检验时需代入原三个方程逐一验证。 五、巩固练习题 解方程组 ⎩ ⎨ ⎧ x+y+z=9 x−y+z=1 2x+y−z=2 (答案: ⎩ ⎨ ⎧ x=2 y=4 z=3 ) 解方程组 ⎩ ⎨ ⎧ 2x+3y+z=6 x−y+2z=−1 x+2y−z=5 (答案: ⎩ ⎨ ⎧ x=2 y=1 z=−1 ) 总结 三元一次方程组的解法本质是「消元转化」,核心是熟练运用加减消元法和代入消元法,将复杂的三元问题转化为已学的二元、一元问题。解题时需注意观察方程特点,选择最优消元对象,减少计算量,同时养成检验的习惯,避免错误。
▶
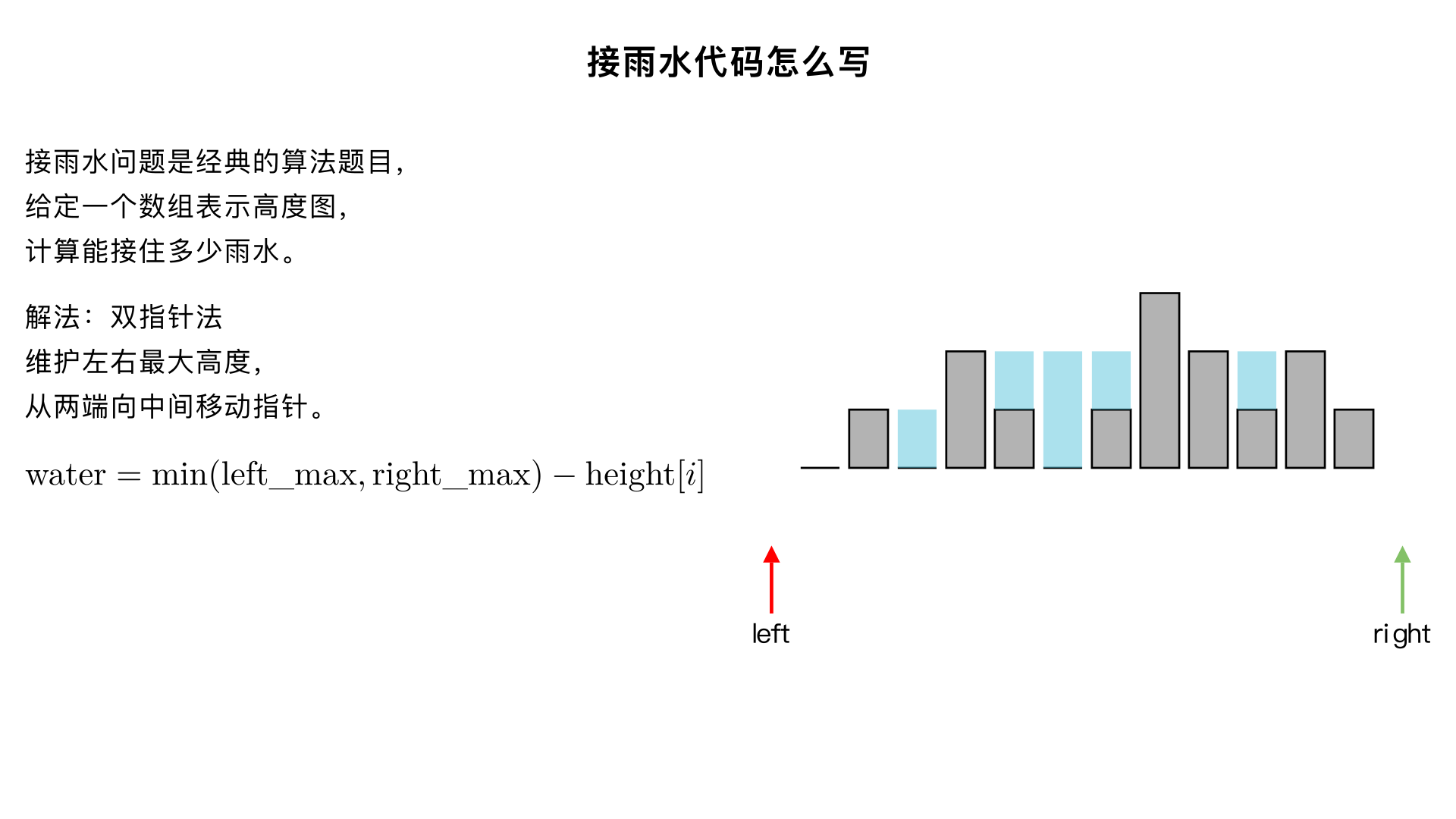
接雨水代码怎么写
▶
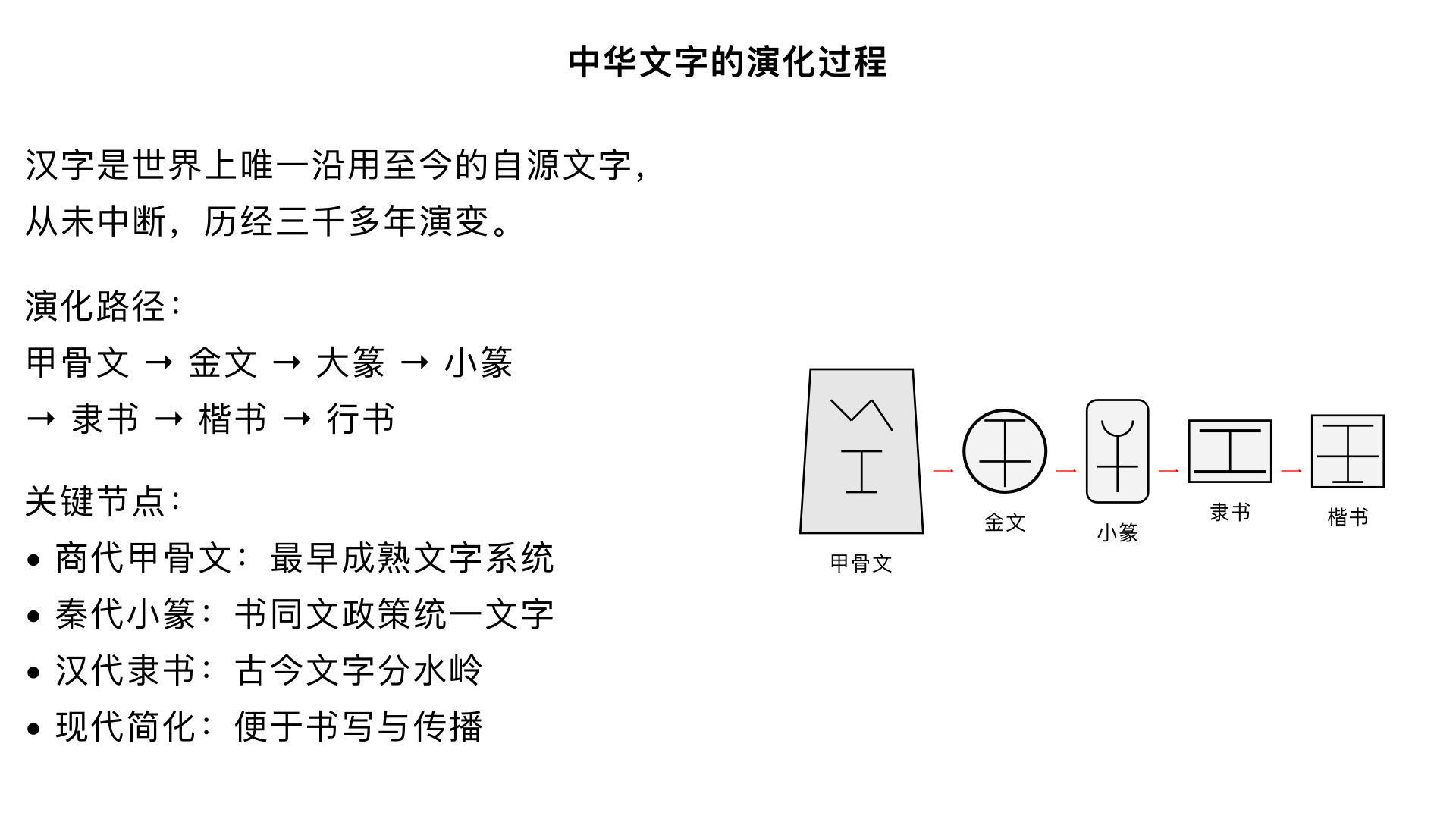
中华文字的演化过程 一、汉字的起源(约 8000 年前) 汉字源头可追溯至新石器时代的刻画符号: 贾湖刻符(约 9000-7800 年前):河南贾湖遗址出土,比甲骨文早 4000 余年,是中国已知最早的文字雏形 仰韶文化陶文(约 7000-5000 年前):陶器上的刻画符号,已具 "标记" 和 "表号" 性质 龙山文化符号(约 4500 年前):结构更复杂,接近成熟文字 汉字形成阶段:大汶口文化中期至龙山文化时期(约 6000-4000 年前),文字系统初步形成 二、古文字阶段(商至秦) 1. 甲骨文(约公元前 14-11 世纪) 刻于龟甲兽骨的占卜文字,已发现 4500 余字,可辨识约 1500 字 特点:象形性强,笔画瘦硬方折,结构不固定(同一字有多种写法) 地位:中国最早的成熟文字系统,标志汉字进入完整记录语言阶段 2. 金文(商周时期) 铸刻于青铜器(主要是钟鼎)上的文字,又称 "钟鼎文" 特点:笔画圆润,字形更饱满,象形性减弱,规范度提高 发展:商晚期铭文简短(不超 50 字),西周鼎盛(如毛公鼎鼎文 497 字) 3. 篆书 大篆(西周晚期): 又称 "籀文",文字规范化尝试,线条均匀,结构整齐 代表作:石鼓文,被视为大篆 "真迹" 小篆(秦代): 秦始皇统一中国后推行 "书同文" 政策,命李斯等人整理的标准字体 特点:笔画圆转匀称,字形长方,彻底符号化,首次官方大规模文字规范 意义:基本消除 "文字异形" 现象,奠定中华文明统一基础 三、今文字阶段(汉代至今) 1. 隶书(秦汉时期) 由小篆简化演变而来,又称 "八分",因 "隶人"(下级官吏)使用得名 秦隶(古隶):小篆的草率写法,是隶书前身 汉隶(成熟隶书): 特点:"蚕头燕尾",笔画方折,字形扁平,彻底脱离象形特征 "隶变":汉字史上里程碑,古文字与今文字分水岭,奠定现代汉字基础 2. 楷书(汉末至魏晋) 由隶书演变而来,又称 "真书" 或 "正书",意为 "标准字体" 特点:字形方正,笔画规整,结构严谨,确立了汉字基本笔画与书写规则 发展: 汉末萌芽,魏晋南北朝成熟,隋唐达到鼎盛(颜柳欧赵 "楷书四大家") 钟繇、王羲之是楷书发展关键人物 3. 辅助字体 草书:隶书的快写体,始于汉代,分 "章草"(带隶意)和 "今草"(连笔更甚),唐代发展为狂草,实用性降低但艺术性增强 行书:介于楷书与草书之间,书写便捷且易辨认,汉末形成,王羲之《兰亭序》被誉为 "天下第一行书" 四、现代汉字的形成 1. 印刷字体的发展 宋体(宋代):为适应印刷发明的字体,笔画横细竖粗,字形方正,成为书籍标准印刷体 明体(明朝):宋体变体,更规整,现代书籍报刊常用 2. 汉字简化历程 历史简化现象:甲骨文时期就存在简体与繁体并存现象,敦煌汉简中也有类似今简体的写法 近代简化运动: 1935 年:国民政府公布《第一批简体字表》,后废止 1956 年:新中国颁布《汉字简化方案》,分四批推行,1964 年编印《简化字总表》,简化 542 个繁体字 简化方法:起用古体(如 "从" 替代 "從")、局部代全体(如 "飞" 替代 "飛")、改换简易声旁(如 "态" 替代 "態") 五、汉字演变的规律 简化:总趋势是笔画减少、结构简化,便于书写 例:"马" 字从甲骨文→金文→小篆→繁体→简体的演变轨迹 声化:形声字比例不断上升(从甲骨文 20% 到现代 90% 以上),表音功能增强 规范化:从甲骨文异体繁多到小篆统一,再到现代标准字,人为规范贯穿始终 重要节点:秦始皇 "书同文"、东汉《熹平石经》、唐代《五经定本》、现代《简化字总表》 六、总结:汉字演化的历史意义 汉字七体演变路径:甲骨文 → 金文 → 大篆 → 小篆 → 隶书 → 楷书 → 行书(草书并行) 从原始刻画到现代简体字,汉字历经3000 多年演变,展现出强大生命力: 它是世界上唯一沿用至今的自源文字,从未中断 它承载着中华文明,是维系民族团结的文化纽带 它的演变反映了中华文化从具象到抽象、从多元到统一的发展历程 核心启示:汉字演化体现了中华文化 "变中求稳" 的智慧,既顺应时代需求不断简化创新,又保持文化根基一脉相承。

▶
七年级数学 / 二元一次方程组 / 消元 —— 解二元一次方程组 一、核心目标 理解 “消元思想” 的本质(将二元一次方程组转化为一元一次方程求解); 掌握两种核心消元方法:代入消元法、加减消元法; 能根据方程组特点选择合适的消元方法,熟练求解二元一次方程组。 二、基础概念回顾 二元一次方程组定义:含有两个未知数,且含未知数的项的次数都是 1 的两个一次方程组成的方程组(如: { x+y=5 2x−y=1 ); 方程组的解:能使方程组中两个方程同时成立的两个未知数的值(如上述方程组的解为 { x=2 y=3 ); 消元思想:通过 “消去一个未知数”,把二元一次方程组转化为已学过的一元一次方程,进而求解的思想(核心:“二元→一元” 的转化)。 三、核心知识点:两种消元方法 (一)代入消元法 1. 适用场景 方程组中某一个方程的未知数系数为 1 或 - 1(便于变形为 “ x=ay+b ” 或 “ y=ax+b ” 的形式)。 2. 解题步骤(口诀:“变、代、解、回、验、写”) 步骤 具体操作 示例(解方程组: ① ② ) 1. 变形 选一个系数为 1/-1 的方程,将其中一个未知数用另一个未知数表示 由①得: y=5−x ③(将 y 用 x 表示) 2. 代入 把变形后的方程代入另一个方程,消去一个未知数 将③代入②: 2x−(5−x)=1 (消去 y,得到一元一次方程) 3. 求解 解一元一次方程,求出一个未知数的值 解 2x−5+x=1 → 3x=6 → x=2 4. 回代 将求出的未知数的值代入变形后的方程,求出另一个未知数 把 x=2 代入③: y=5−2=3 5. 检验 把两个未知数的值代入原方程组,验证是否同时成立 ①: 2+3=5 (成立);②: 2×2−3=1 (成立) 6. 写解 写出方程组的解(用大括号表示) { x=2 y=3 3. 易错点提醒 代入时要注意 “整体代入”,避免漏乘括号(如示例中代入时需写 “ 2x−(5−x) ”,而非 “ 2x−5−x ”); 回代时需代入 “变形后的方程” 或 “原方程”,不可代入化简过程中出错的方程。 (二)加减消元法 1. 适用场景 方程组中某一个未知数的系数相等或互为相反数(或系数成倍数关系,可通过乘系数转化为相等或相反)。 2. 解题步骤(口诀:“化同 / 反、加 / 减、解、回、验、写”) 步骤 具体操作 示例 1(系数相反): ① ② 示例 2(系数成倍数): ① ② 1. 化同 / 反 若未知数系数不相等也不相反,给方程乘适当的数,使某一未知数系数相等或相反 ①中 y 的系数为 2,②中 y 的系数为 - 2(互为相反数),无需变形 ②中 x 的系数为 1,①中 x 的系数为 2,给②乘 2: 2x+8y=26 ③ 2. 加 / 减 系数相反→两方程相加(消去该未知数);系数相等→两方程相减 ①+②: (3x+2y)+(5x−2y)=13+11 (消去 y) ③-①: (2x+8y)−(2x+3y)=26−16 (消去 x) 3. 求解 解一元一次方程 8x=24 → x=3 5y=10 → y=2 4. 回代 代入原方程求另一个未知数 把 x=3 代入①: 3×3+2y=13 → y=2 把 y=2 代入②: x+4×2=13 → x=5 5. 检验 验证解是否满足原方程组 ①: 9+4=13 ;②: 15−4=11 (均成立) ①: 10+6=16 ;②: 5+8=13 (均成立) 6. 写解 写出最终解 { x=3 y=2 { x=5 y=2 3. 关键技巧 加减时要注意 “等式两边同时加减”,符号不要出错(如系数相反时相加,系数相同时相减); 若需乘系数变形,要给方程所有项乘同一个数(避免漏乘常数项,如示例 2 中②乘 2 时,13 也要乘 2 得 26)。 四、方法选择技巧 方程组特点 推荐方法 举例 某未知数系数为 1 或 - 1 代入消元法 { y=2x−3 3x+2y=8 某未知数系数相等或相反 加减消元法 { 2x+3y=7 2x−5y=−1 (x 系数相等,用减法) 系数成倍数关系 加减消元法(先变形) { 3x+4y=16 5x−6y=33 (给①乘 3,②乘 2,使 y 系数为 12 和 - 12) 五、易错点汇总 代入消元时漏乘括号(如将 “ y=3−2x ” 代入 “ 3x+2y=5 ” 时,误写为 “ 3x+6−2x=5 ”,正确应为 “ 3x+2(3−2x)=3x+6−4x=5 ”); 加减消元时符号错误(如系数相反时误用减法,系数相同时误用加法); 变形时漏乘常数项(如给 “ x+2y=3 ” 乘 2 时,误写为 “ 2x+2y=6 ”,正确应为 “ 2x+4y=6 ”); 忘记检验解的正确性(尤其当方程变形步骤较多时,检验可避免计算错误)。 六、基础练习(分层设计) 1. 基础题(直接应用方法) 解下列方程组:(1) { x=3y+2 2x+y=11 (代入消元法)(2) { 3x+2y=19 3x−2y=5 (加减消元法) 2. 提高题(需变形后消元) 解下列方程组:(1) { 2x+3y=12 5x−6y=3 (2) { 2 x + 3 y =2 3x−2y=8 (先去分母变形) 参考答案 (1) { x=5 y=1 ;(2) { x=4 y= 2 7 (1) { x=3 y=2 ;(2) { x=4 y=2 七、总结 解二元一次方程组的核心是 “消元”,关键是根据方程组的特点选择合适的方法: 有系数为 1/-1 的方程→优先用代入消元法; 未知数系数相等 / 相反 / 成倍数→优先用加减消元法。 解题时需牢记步骤,注意符号和漏乘问题,检验是确保结果正确的重要环节。通过反复练习,可熟练掌握 “二元→一元” 的转化思维,为后续解决实际问题奠定基础。

▶
九年级化学 / 开展低碳行动 / 二氧化碳的排放 一、核心知识点(九年级化学课标要求) 1. 二氧化碳的主要排放源(化学视角) (1)化石燃料燃烧(最主要来源) 化石燃料(煤、石油、天然气)的组成:含碳元素(C),燃烧时与氧气反应生成 CO₂,释放能量。 关键化学方程式: 煤(主要成分 C): 点 燃 (充分燃烧); 点 燃 (不充分燃烧,后续 CO 仍会转化为 CO₂) 天然气(主要成分 CH₄): 点 燃 石油(如汽油、柴油,含 C、H 元素):以辛烷(C₈H₁₈)为例, 点 燃 应用场景:工业生产(工厂锅炉)、交通运输(汽车、飞机)、日常生活(取暖、做饭)。 (2)工业生产过程排放 煅烧石灰石(制备生石灰): 高 温 (建筑、化工行业常用) 水泥生产、钢铁冶炼等:原料中含碳酸盐或碳元素,生产中会释放 CO₂。 (3)生物呼吸作用 动植物及微生物的呼吸:消耗 O₂,释放 CO₂,反应式: 酶 能 量 特点:属于自然循环的一部分,但若植被破坏(植物光合作用吸收 CO₂减少),会导致呼吸排放的 CO₂无法被有效吸收。 2. 二氧化碳排放与环境的关系 (1)温室效应的成因 CO₂是主要温室气体,其分子能吸收地面反射的红外线,减少热量散失,导致全球气温升高。 关联知识点:温室气体还包括甲烷(CH₄)、臭氧(O₃)等,但 CO₂排放量大、影响范围广。 (2)过量排放的危害(化学与环境跨学科) 全球变暖:冰川融化、海平面上升、极端天气增多。 生态破坏:影响农作物生长(温度、降水变化)、海洋酸化(CO₂溶于水生成碳酸: CO 2 +H 2 O⇌H 2 CO 3 )。 3. 低碳行动的化学原理与依据 低碳核心:减少 CO₂排放(控制碳元素的氧化反应)、增加 CO₂吸收(利用碳循环)。 化学逻辑: 减少化石燃料使用:降低碳元素的燃烧反应速率和总量。 开发新能源:使用不含碳或含碳量极低的能源,避免 CO₂生成。 碳吸收:利用化学反应(如光合作用、碳酸盐转化)将 CO₂固定。 二、知识延伸(联系实际应用) 1. 常见碳排放的 “化学量化”(简单计算) 例 1:1kg 甲烷(CH₄)完全燃烧生成 CO₂的质量?解:设生成 CO₂质量为 x 点 燃 16 441kg x 44 16 = x 1kg → x=2.75kg (说明天然气燃烧的碳排放强度低于煤、石油) 例 2:煅烧 100t 石灰石(CaCO₃纯度 90%),最多排放 CO₂多少吨?解:纯 CaCO₃质量 = 100t×90%=90t设生成 CO₂质量为 y 高 温 100 4490t y 44 100 = y 90t → y=39.6t (体现工业生产的碳排放规模) 2. 低碳行动的化学实践(可操作方案) (1)减少排放的化学手段 优化燃烧技术:让化石燃料充分燃烧(如工业锅炉安装脱硫脱硝装置,同时促进完全燃烧),减少 CO 和 CO₂排放。 替代能源的化学应用: 氢能(H₂): 点 燃 ,无 CO₂排放,用于新能源汽车、燃料电池。 太阳能、风能:转化为电能,避免化石燃料燃烧(间接减少 CO₂排放)。 工业减排:用化学方法替代高排放工艺(如用新型催化剂降低工业反应的能耗,减少化石燃料消耗)。 (2)增加 CO₂吸收的化学途径 植物光合作用: 光 照 、 叶 绿 素 ,植树造林、培育绿色植物(利用化学变化固定 CO₂)。 人工固碳:利用化学反应吸收 CO₂(如用氢氧化钙溶液: Ca(OH) 2 +CO 2 =CaCO 3 ↓+H 2 O ,适用于工业尾气处理)。 碳捕捉与封存(CCS 技术):将工业排放的 CO₂通过化学吸收剂捕获,压缩后封存于地下或海底(九年级拓展知识点)。 (3)日常生活中的低碳化学 低碳出行:选择自行车、新能源汽车(避免汽油燃烧生成 CO₂)。 节约用电:减少火电消耗(火电依赖煤燃烧),间接减少 CO₂排放。 垃圾分类:可回收物(如塑料、纸张)回收利用,减少新原料生产(如塑料生产需石油,回收可降低化石燃料消耗)。 三、易错点与重难点突破 1. 易错点辨析 误区 1:“所有燃烧都产生 CO₂”→ 纠正:不含碳元素的物质燃烧(如 H₂、酒精燃烧生成 CO₂和 H₂O,但 H₂燃烧只生成 H₂O),无 CO₂排放。 误区 2:“生物呼吸排放 CO₂是造成温室效应的主要原因”→ 纠正:自然呼吸排放的 CO₂与植物光合作用形成循环,过量排放主要来自化石燃料燃烧和工业生产。 误区 3:“低碳就是完全不排放 CO₂”→ 纠正:低碳是 “低强度、可持续” 的排放,核心是减少人为新增 CO₂,维持碳循环平衡。 2. 重难点突破 关键:理解 “碳循环” 与化学变化的关系 ——CO₂的排放(燃烧、分解反应)和吸收(化合、光合作用)都是化学变化,低碳行动本质是通过控制化学变化的速率和方向,实现碳平衡。 应用:结合化学方程式分析不同能源的碳排放强度,判断低碳方案的合理性(如对比煤、天然气、氢能的燃烧产物,选择低碳能源)。 四、中考真题衔接(示例) (2023・某省中考)“低碳生活” 是现代社会的主流理念,下列做法不符合低碳理念的是( )A. 用新能源汽车替代燃油汽车 B. 焚烧秸秆增加农田肥力C. 垃圾分类回收利用 D. 室内照明使用 LED 灯答案:B(解析:焚烧秸秆会产生 CO₂和有害气体,增加碳排放,且污染环境) (2022・某省中考)请用化学方程式解释下列现象:(1)天然气用作家用燃料时,能减少碳排放(与煤相比):__________(2)工业上煅烧石灰石制备生石灰时,会产生 CO₂:__________答案:(1) 点 燃 (相同质量的 CH₄和煤,CH₄燃烧生成的 CO₂更少);(2) 高 温 五、实践活动建议(结合课堂与生活) 小组调查:统计家庭 1 周内的碳排放来源(如开车里程、用电度数、燃气使用量),结合化学方程式估算 CO₂排放量,提出 3 条低碳改进方案。 实验探究:设计 “不同燃料燃烧的碳排放对比” 实验(如点燃等质量的煤块、木炭、酒精,用澄清石灰水吸收 CO₂,观察浑浊程度,分析碳排放差异)。 主题辩论:“化学技术能否解决碳排放问题”,结合所学知识点(新能源、化学固碳、工业减排)展开讨论,培养科学思维。
▶
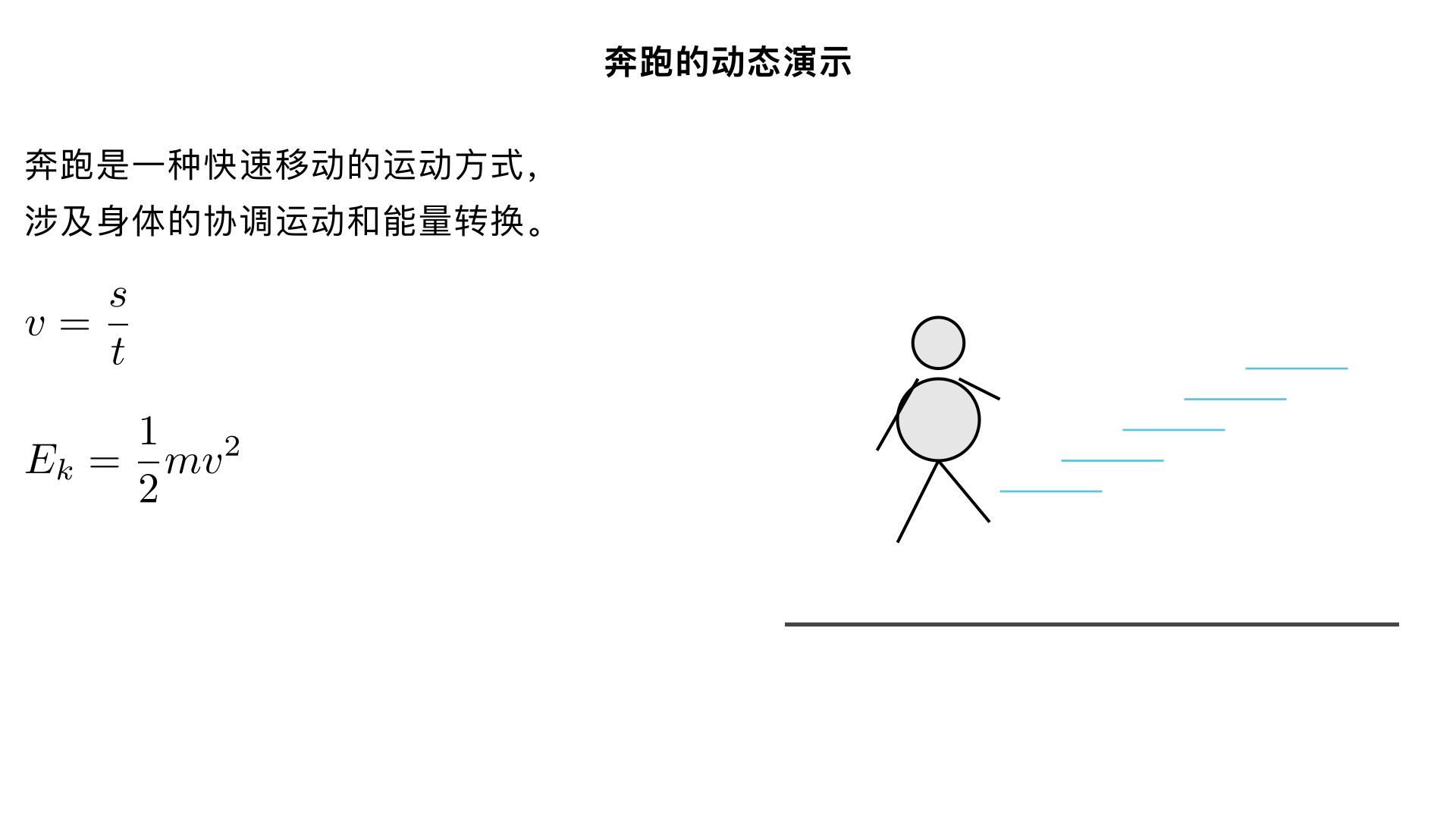
生成一个奔跑的视频
▶
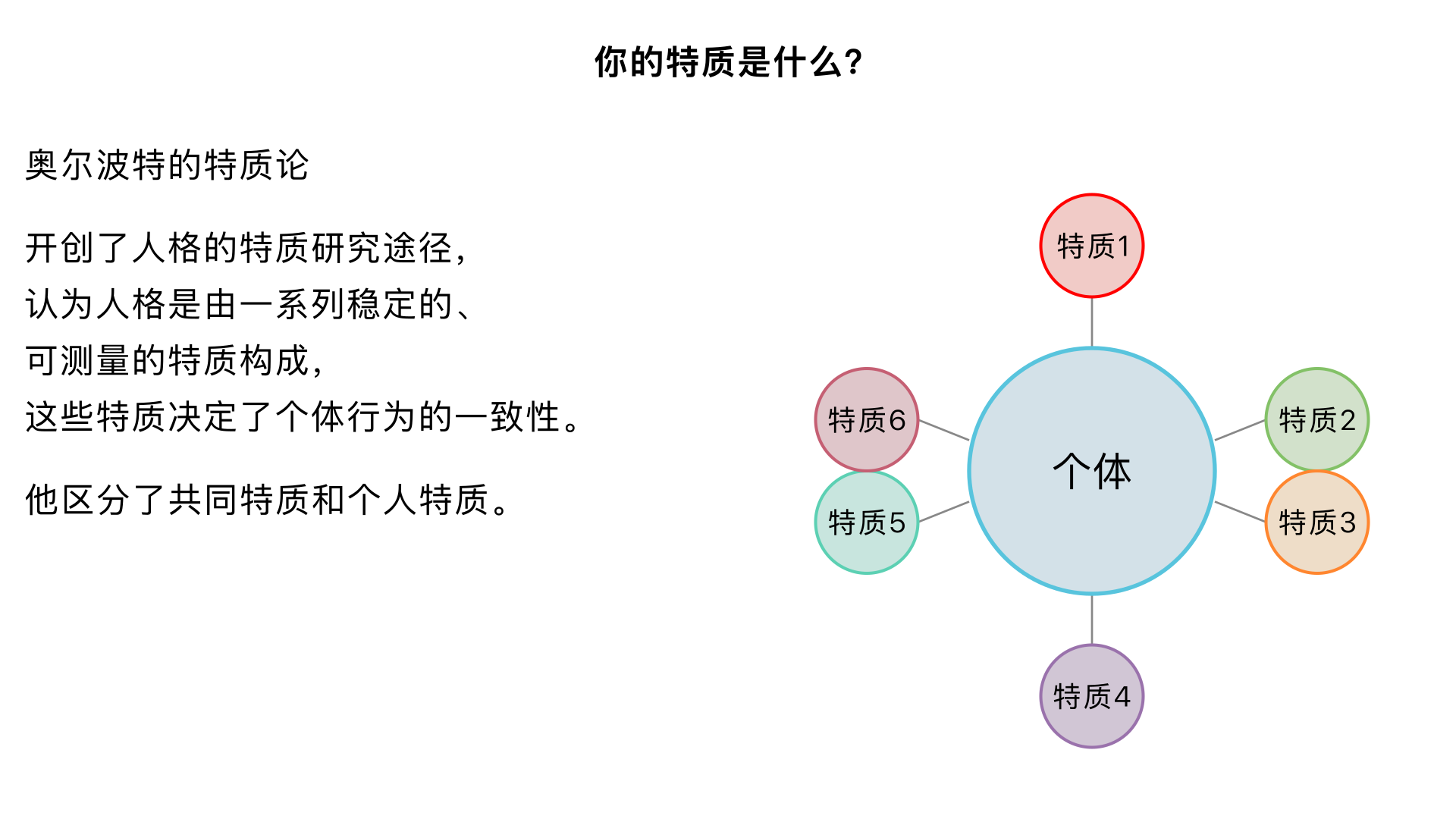
你的特质是什么? (奥尔波特的“特质论”) 主要内容:开创了人格的特质研究途径,认为人格是由一系列稳定的、可测量的特质构成,这些特质决定了个体行为的一致性。他区分了共同特质和个人特质。

▶
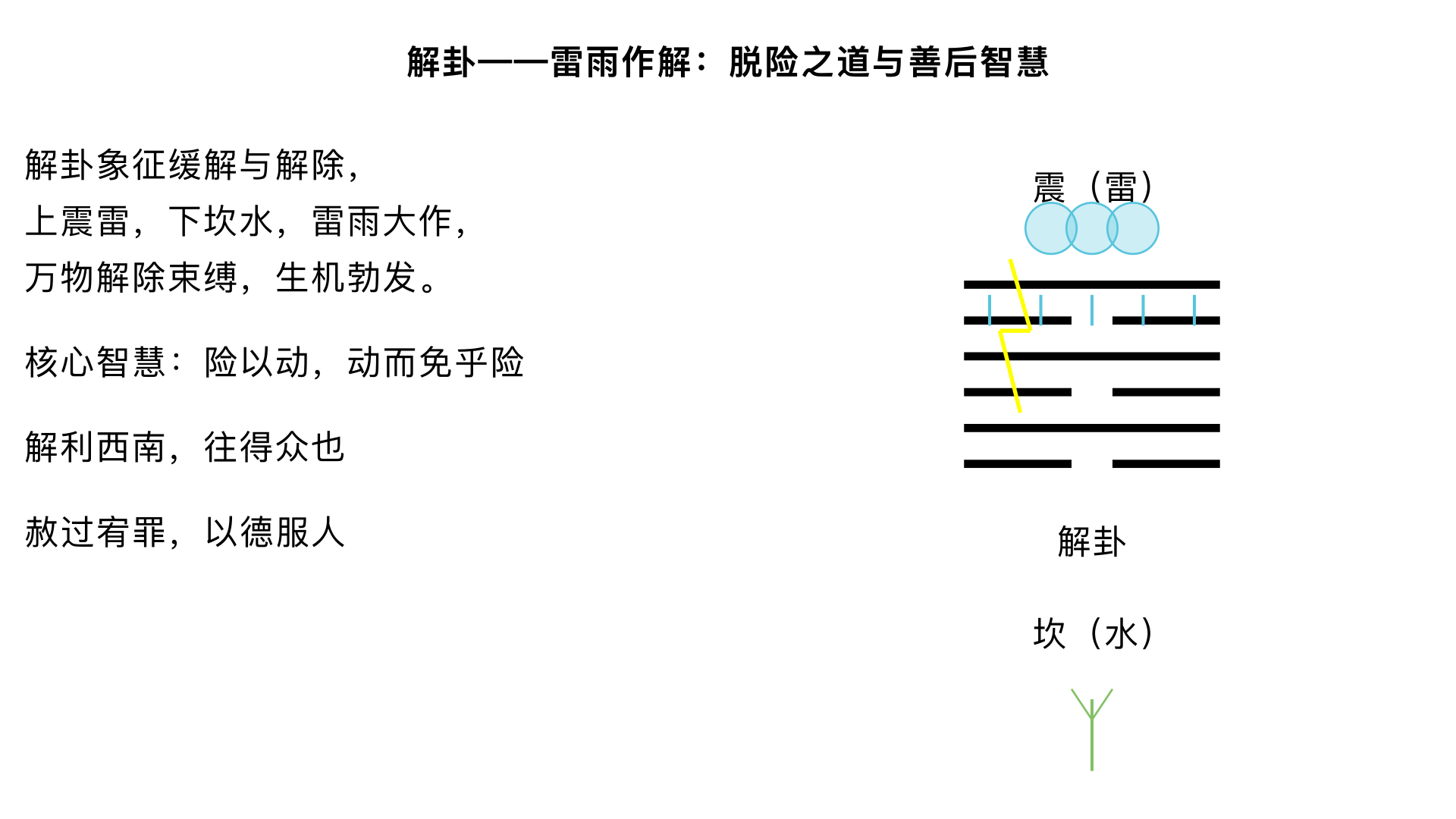
讲解:解卦——雷雨作解:脱险之道与善后智慧 一、卦序逻辑:从艰难到缓解 1. 《序卦传》的必然转化 “蹇者,难也。物不可以终难,故受之以解。解者,缓也。” 蹇卦(水山蹇)象征艰难险阻 → 但事物不会永远处于艰难中 → 解卦(雷水解)象征缓解、解除 金景芳指出:这体现了《周易》“穷则变,变则通”的辩证思想 2. 蹇卦与解卦的综卦关系 蹇卦(䷦):上坎下艮,山上有水,险阻在前 解卦(䷧):上震下坎,雷雨作,百果草木皆甲坼(生机勃发) 二卦互为综卦(将蹇卦上下颠倒即得解卦),表明险难与解除是同一过程的不同阶段 二、解卦(雷水解)卦象的解放之象 1. “雷雨作”的生机勃发 基本卦象:上震雷,下坎水 → 雷雨大作,滋润万物 自然象征: 冬季(坎为水,为冬)过后,春雷(震为雷,为春)震动,雨水降临,冰消雪融 万物解除束缚,破壳而出(“百果草木皆甲坼”) 金景芳引申:此象喻示政治严苛(坎险)之后,仁政施行(震动),万民获得新生 2. 卦德分析与行动原则 下坎为险,上震为动 → 动而出险 《彖传》:“解,险以动,动而免乎险,解。” 核心智慧:在险境中积极行动,通过行动脱离险境 3. 爻位结构中的隐患 六三阴柔失正,上六无应 → 提示解难后可能产生新的问题 九二、九四阳刚有力,为解难主力 金景芳提醒:解卦不是一劳永逸,需防“致寇至” 三、彖传精解:解困之道 “解,险以动,动而免乎险,解。 解利西南,往得众也。 其来复吉,乃得中也。 有攸往夙吉,往有功也。 天地解而雷雨作,雷雨作而百果草木皆甲坼。 解之时大矣哉!” 1. “险以动,动而免乎险”的行动哲学 辩证关系:险境中行动(险以动),行动才能脱险(动而免乎险) 历史例证:刘邦被围荥阳,用陈平计突围(动),终免于险 反面教材:宋襄公“不鼓不成列”,坐失战机,未“动而免乎险” 2. “解利西南,往得众也”的民心指向 西南象征:坤方,平地,众庶(坤为众) “往得众”:前往西南可得民众支持 与蹇卦呼应:蹇卦“利西南”为避险,解卦“利西南”为得众 政治智慧:解难后需争取民心,如武王克商后“释箕子囚,封比干墓” 3. “其来复吉,乃得中也”的回归原则 “来复”:回归常态,恢复秩序 “得中”:符合中道(指九二居中) 政策启示:动乱平息后,应休养生息,恢复常规 历史例证:汉初萧何“与民休息”,是“其来复吉” 4. “有攸往夙吉,往有功也”的时效原则 “夙吉”:及早行动则吉(夙,早也) “往有功”:前往可建功业 战术要求:解决遗留问题要迅速,如周公东征速平管蔡之乱 5. “天地解而雷雨作…”的自然意象升华 将人事解脱与天地生化相联系 寓意:政治解困如雷雨滋润万物,带来生机 金景芳阐发:解卦蕴含“革命解放”的正当性,如汤武革命“顺乎天而应乎人” 6. “解之时大矣哉!”的赞叹 解卦的时义太重大了! 强调:把握解难时机的重要性,早则不及,迟则生变 四、大象传:“赦过宥罪”的宽恕精神 “雷雨作,解。君子以赦过宥罪。” 1. “赦过宥罪”的政治智慧 赦过:赦免无心过失 宥罪:宽恕有意罪过(但非免除惩罚,是减刑) 与《尚书》互证:“眚灾肆赦,怙终贼刑”(过失犯罪可赦,惯犯严惩) 2. 历史应用 汉文帝废肉刑:体现“宥罪”精神 唐太宗纵囚:风险之举,但收服人心 现代意义:战后和解、转型正义中的宽恕政策 3. 金景芳提醒:“赦过宥罪”不是无原则宽大,而是“解”后争取人心的策略 五、爻辞精析:解难的六个要点 解卦六爻侧重解难之后如何巩固成果、防止反复,是一套“善后指南”。 1. 初六:无咎。 简短爻辞,深意存焉:初六阴柔居解始,与九四正应 “无咎”条件:解难之初,低调顺从(上应九四),不争功,故无咎 象征:普通民众在解放后安分守己,可得无咎 历史情景:商民在周克商后,服从新朝,得保平安 2. 九二:田获三狐,得黄矢,贞吉。 “田获三狐”:田猎获得多只狐狸(狐象征小人、隐患) “得黄矢”:得到黄色箭矢(黄为中色,矢为直,象征中直之道) 爻象:九二阳刚居中,为解难主力 含义: 解难后需肃清余孽(三狐) 方法要中正(黄矢) 历史例证:周公诛管叔、放蔡叔、囚霍叔(三狐),但存中道(不滥杀) 3. 六三:负且乘,致寇至,贞吝。 全卦核心警示,源自孔子在《系辞传》中的重点阐发 生动画面: “负且乘”:背着财物坐在车上(小人得志,炫耀富贵) “致寇至”:招致强盗来抢 爻象:六三阴柔失正,居下卦之上,象征才德不配位的小人 孔子阐发(《系辞上》第八章): “作《易》者其知盗乎?…小人而乘君子之器,盗思夺之矣。” 揭示:德不配位,必招灾祸 现实意义:企业危机后,管理者若炫耀成功,可能引发新的危机 4. 九四:解而拇,朋至斯孚。 “解而拇”:解开你大脚趾的束缚(拇,足大趾,指初六) “朋至斯孚”:朋友到来,以诚信相待 爻象:九四阳居阴位,刚柔相济,下应初六 策略:解脱基层束缚(解而拇),则民众(朋)诚心归附(斯孚) 政策对应:汉高祖“约法三章”,解秦苛法,得关中民心 5. 六五:君子维有解,吉。有孚于小人。 “君子维有解”:君子被捆绑又得解脱(维,系也) “吉”:吉祥 “有孚于小人”:以诚信感化小人 爻象:六五柔中居尊,下应九二,处震卦中位 领袖之道: 自身曾受困(维),终得解 掌权后不报复,以诚信待小人(包括曾经的敌人) 历史典范:齐桓公不记管仲射钩之仇,任用为相,终成霸业 6. 上六:公用射隼于高墉之上,获之,无不利。 生动比喻: “公用射隼”:王公射杀凶鸟(隼,猛禽,象征残存的恶势力) “于高墉之上”:在高墙上(墉,城墙,象征险要位置) 爻象:上六处解之终,仍有隐患(隼)居高墉,需彻底清除 “获之,无不利”:擒获它,无所不利 历史例证:汉武帝彻底解决诸侯王问题(推恩令),巩固统一 金景芳总结:解卦以“射隼”作结,强调解难的彻底性 六、解卦的解难智慧总论 1. 行动原则:“险以动,动而免乎险” 积极行动,脱出险境 2. 政治方向:“利西南,往得众” 解难后争取民心,稳定大局 3. 善后要务: 肃清余孽(田获三狐) 防止炫耀(负且乘) 解脱民困(解而拇) 感化小人(有孚于小人) 清除顽敌(射隼高墉) 4. 宽恕精神:“赦过宥罪” 但宽恕有度,不是无限赦免 5. 金景芳总结:解卦是儒家“拨乱反正”思想的体现,强调解难要彻底,善后要谨慎,治国要以德服人。
▶