T
Teach Me AnythingTMA
Video History
Page 15 / 43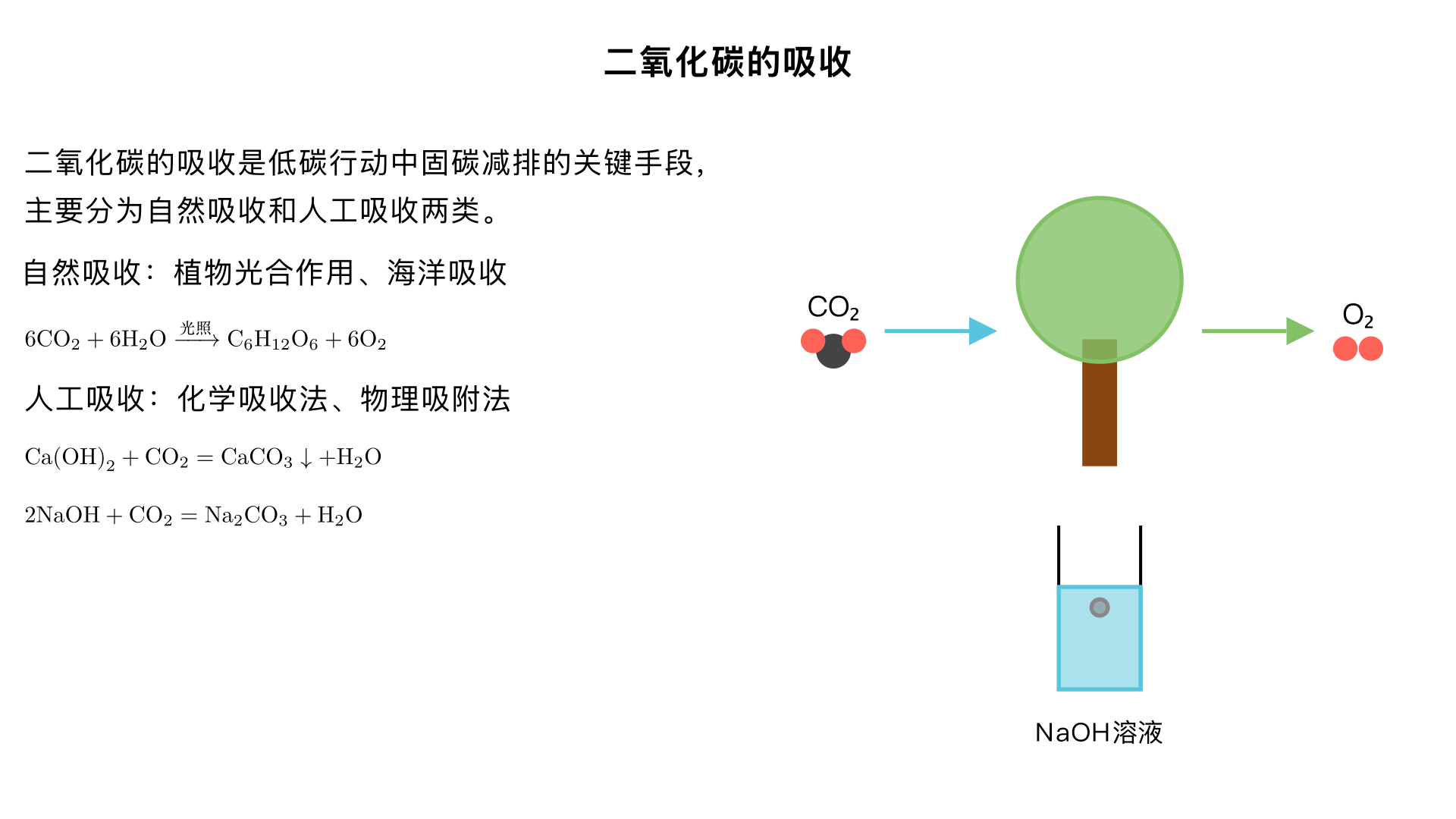
▶
九年级化学 / 开展低碳行动 / 二氧化碳的吸收 核心结论 二氧化碳的吸收是低碳行动中 “固碳减排” 的关键手段,主要分为自然吸收(生物固碳) 和人工吸收(化学 / 物理固碳) 两类,核心原理是通过化学反应或物理作用将 CO₂转化为稳定物质或储存起来,减少大气中 CO₂浓度。 一、自然吸收(生物固碳)—— 地球的 “天然碳汇” 1. 植物的光合作用(最主要途径) 原理:绿色植物通过叶绿体,利用光能将 CO₂和水转化为有机物(如葡萄糖),释放氧气,实现 CO₂的 “固定”。 化学方程式:6CO₂ + 6H₂O 叶 绿 体 光 照 C₆H₁₂O₆(葡萄糖)+ 6O₂ 关键细节: 吸收主体:森林、草原、农作物、藻类等(森林是 “地球之肺”,占全球生物固碳量的 60% 以上)。 应用场景:植树造林、退耕还林、保护湿地(湿地植物 + 微生物共同固碳)、海洋藻类养殖。 2. 海洋的吸收(第二大碳汇) 原理: 物理溶解:CO₂可溶于海水,形成碳酸(H₂CO₃); 生物作用:海洋浮游植物的光合作用吸收 CO₂,海洋生物死亡后遗体沉积海底,将碳长期储存。 注意:过量 CO₂溶解会导致海水酸化(碳酸电离出 H⁺),影响海洋生物生存,因此海洋吸收存在 “环境上限”。 二、人工吸收(技术固碳)—— 低碳行动的 “主动手段” 1. 化学吸收法(实验室 + 工业常用) (1)碱液吸收(最经典) 原理:CO₂是酸性氧化物,与碱溶液反应生成盐和水,实现 “化学固定”。 常见反应与应用: 吸收剂 化学方程式 应用场景 澄清石灰水(Ca (OH)₂) Ca (OH)₂ + CO₂ = CaCO₃↓(白色沉淀)+ H₂O 实验室检验 CO₂(石灰水变浑浊) 氢氧化钠溶液(NaOH) 2NaOH + CO₂ = Na₂CO₃ + H₂O(CO₂少量);Na₂CO₃ + CO₂ + H₂O = 2NaHCO₃(CO₂过量) 工业尾气处理(如电厂、钢厂 CO₂回收)、潜水艇换气系统 关键对比:NaOH 溶液吸收 CO₂的能力比澄清石灰水强(因为 Ca (OH)₂溶解度小,浓度低),所以工业上优先用 NaOH 溶液,实验室仅用石灰水检验。 (2)碳酸盐吸收(长效固碳) 原理:CO₂与碳酸盐反应生成碳酸氢盐,或直接转化为稳定的碳酸盐矿物(如碳酸钙、碳酸镁)。 示例:将 CO₂通入石灰乳(浓 Ca (OH)₂悬浊液),生成 CaCO₃沉淀,可用于生产建筑材料(如石灰石、水泥),实现 “碳封存 + 资源利用”。 2. 物理吸附法 原理:利用多孔材料(如活性炭、沸石、分子筛)的吸附性,将 CO₂气体吸附在材料表面,实现分离储存。 应用场景:天然气提纯(去除 CO₂杂质)、室内空气净化(小型 CO₂吸附装置)。 优点:操作简单、无化学副产物;缺点:吸附量有限,需要定期再生材料(加热或减压释放 CO₂后重新使用)。 3. 工业固碳技术(前沿应用) 碳捕捉与封存(CCS 技术): 捕捉:从电厂、水泥厂等工业尾气中分离 CO₂(用化学吸收或物理吸附法); 运输:通过管道或高压容器将液态 CO₂运输到储存地点; 封存:将 CO₂注入地下深层岩层(如枯竭油田、盐矿层),使其长期稳定储存,不进入大气。 碳转化技术:将 CO₂与氢气、甲烷等反应,转化为甲醇、乙醇、塑料等化工产品,实现 “变废为宝”(如 CO₂ + 3H₂ 催 化 剂 CH₃OH + H₂O)。 三、低碳行动中的实际应用(知识落地) 个人层面:爱护绿植、参与植树活动(助力自然固碳);减少一次性用品使用(间接减少 CO₂排放,降低固碳压力)。 社会层面: 城市绿化:增加公园、道路绿化带面积,提升城市 “碳汇能力”; 工业减排:推广 NaOH 溶液处理工业尾气、发展 CCS 技术; 新能源替代:减少化石燃料使用(从源头减少 CO₂排放),配合固碳技术形成 “减排 + 固碳” 闭环。 四、易错点辨析 误区:“澄清石灰水可用于大量吸收 CO₂”—— 错误!澄清石灰水 Ca (OH)₂溶解度小,浓度低,仅能检验 CO₂,大量吸收需用 NaOH 溶液。 误区:“植物光合作用吸收 CO₂,所以种树越多越好”—— 不完全正确!植物死亡后若被分解(如腐烂、燃烧),会重新释放 CO₂;只有长期存活的森林(如原始森林)才能实现 “长期固碳”。 关键区分:“吸收 CO₂”vs“减少 CO₂排放”—— 吸收是 “清除已有的 CO₂”,减排是 “减少新增的 CO₂”,二者结合才是完整的低碳行动。
▶
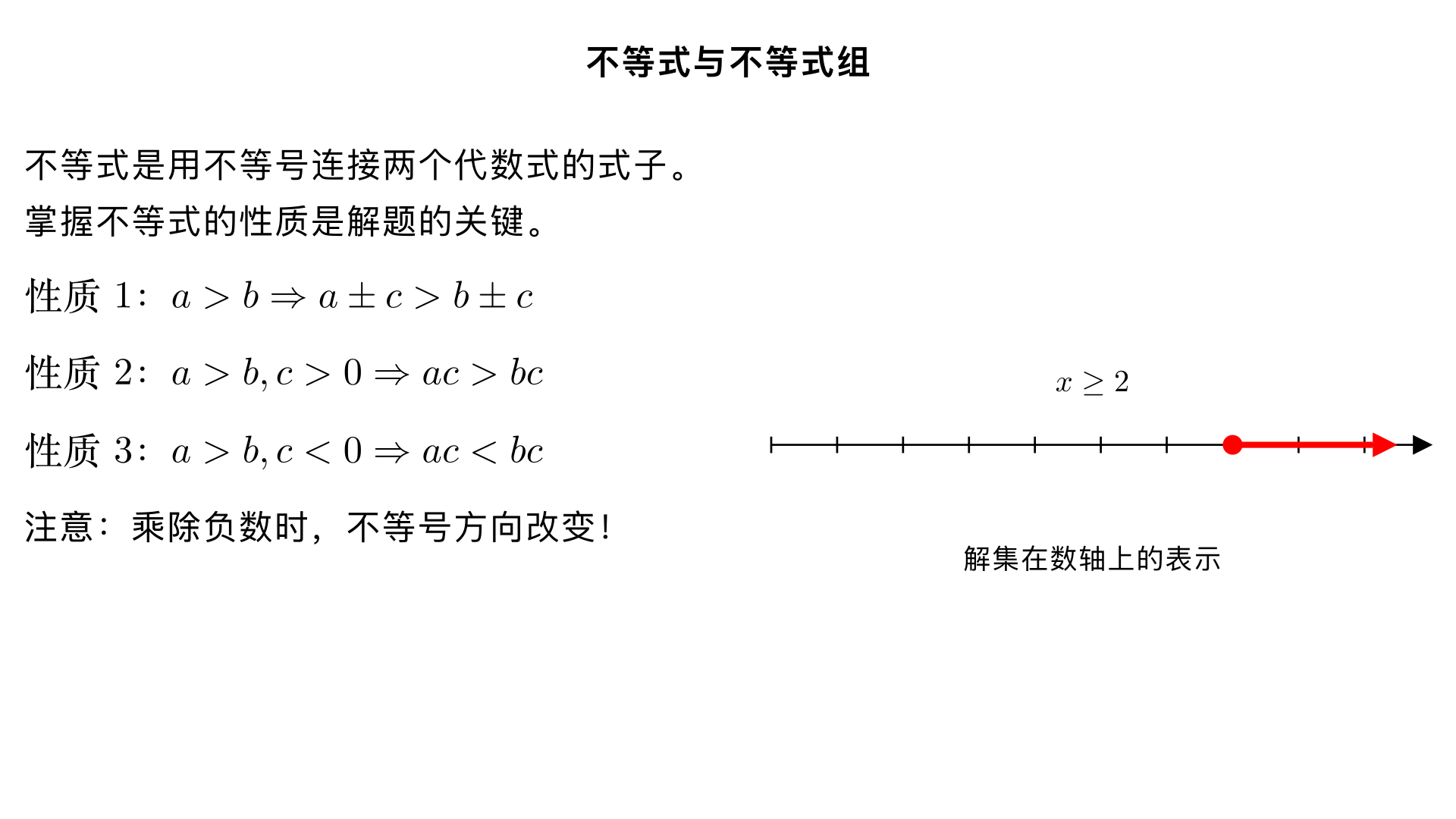
七年级数学 / 不等式与不等式组 / 不等式 一、不等式的定义 用不等号连接两个代数式(或表示数量关系)的式子,叫做不等式。 常见不等号:>(大于)、<(小于)、≥(大于或等于,也叫 “不小于”)、≤(小于或等于,也叫 “不大于”)、≠(不等于) 示例:3>2、x+1≤5、2a≠3b、m-3≥0 二、不等式的基本性质(核心考点) 不等式的性质是变形、求解的依据,共 3 条,重点注意性质 3 的变号规则: 性质 1:同向加减不变号 不等式两边同时加(或减)同一个数(或同一个整式),不等号的方向不变。 字母表示:若 a>b,则 a±c>b±c;若 a<b,则 a±c<b±c 示例:5>3→5+2>3+2(7>5)、5-1>3-1(4>2) 性质 2:同向乘除正数不变号 不等式两边同时乘(或除以)同一个正数,不等号的方向不变。 字母表示:若 a>b、c>0,则 ac>bc、 > ;若 a<b、c>0,则 ac<bc、 < 示例:4>2→4×3>2×3(12>6)、4÷2>2÷2(2>1) 性质 3:同向乘除负数必变号(易错点) 不等式两边同时乘(或除以)同一个负数,不等号的方向必须改变(>变<、<变>、≥变≤、≤变≥)。 字母表示:若 a>b、c<0,则 ac<bc、 < ;若 a<b、c<0,则 ac>bc、 > 示例:6>4→6×(-1)<4×(-1)(-6<-4)、6÷(-2)<4÷(-2)(-3<-2) 三、不等式的解与解集 1. 不等式的解 能使不等式成立的未知数的每一个具体值,叫做不等式的一个解。 示例:不等式 x+2>5,x=4(4+2=6>5)、x=5(5+2=7>5),都是它的解(解有无数个) 2. 不等式的解集 能使不等式成立的所有未知数的值的集合,叫做不等式的解集(解集是 “所有解的整体”,解是解集里的单个值)。 解集表示方法: 文字描述:如 “x 大于 3”“x 小于或等于 2” 符号表示:如 x>3、x≤2、1<x<5(x 大于 1 且小于 5) 数轴表示(直观,必考): 步骤:①画数轴;②找解集对应 “分界点”(如 x>3 的分界点是 3);③定 “空心 / 实心”:解集含分界点(≥、≤)用实心圆点,不含分界点(>、<)用空心圆圈;④定方向:解集是 “大于” 向右画,“小于” 向左画。 示例:x≥2(实心圆点在 2,向右延伸)、x<-1(空心圆圈在 - 1,向左延伸) 四、一元一次不等式(基础题型) 1. 定义 只含一个未知数,且未知数的次数是1,不等号两边都是整式的不等式,叫做一元一次不等式。 特征:①单未知数;②未知数次数 = 1;③无分式(分母不含未知数) 示例:3x+1>0(是)、2x-5≤3(是)、 > (不是,分母含 x)、2x²+3<5(不是,未知数次数 2) 2. 求解步骤(5 步,类比一元一次方程,重点注意变号) 去分母:两边同乘所有分母的最小公倍数,若公倍数是负数,需改变不等号方向;注意 “漏乘常数项”(如 > ,去分母得 x+2>6,别漏乘 1)。 去括号:按去括号法则,括号前是负号,括号内各项要变号。 移项:把含未知数的项移到左边,常数项移到右边,移项时必须改变该项符号(同方程移项规则)。 合并同类项:同类项合并,化为 “ax>b”“ax<b”“ax≥b”“ax≤b”(a≠0)的形式。 系数化为 1:两边同除以未知数的系数 a,若 a<0,需改变不等号方向;a>0,方向不变。 示例:解不等式 2 (x-1)+3≤5x+1 ①去括号:2x-2+3≤5x+1 ②移项:2x-5x≤1+2-3 ③合并同类项:-3x≤0 ④系数化为 1(a=-3<0,变号):x≥0 五、常见易错点 用性质 3 时忘变号:乘除负数后,不等号方向未改(如由 - 2x>4 得 x>-2,错误,正确是 x<-2)。 数轴表示错误:含分界点用空心、不含分界点用实心,或方向画反。 去分母漏乘:只乘含分母的项,漏乘常数项(如 > ,错写为 x-2>3,正确是 x-6>3)。 移项忘变号:如由 3x+5>2x-1,错写为 3x-2x>-1+5,正确是 3x-2x>-1-5。
▶
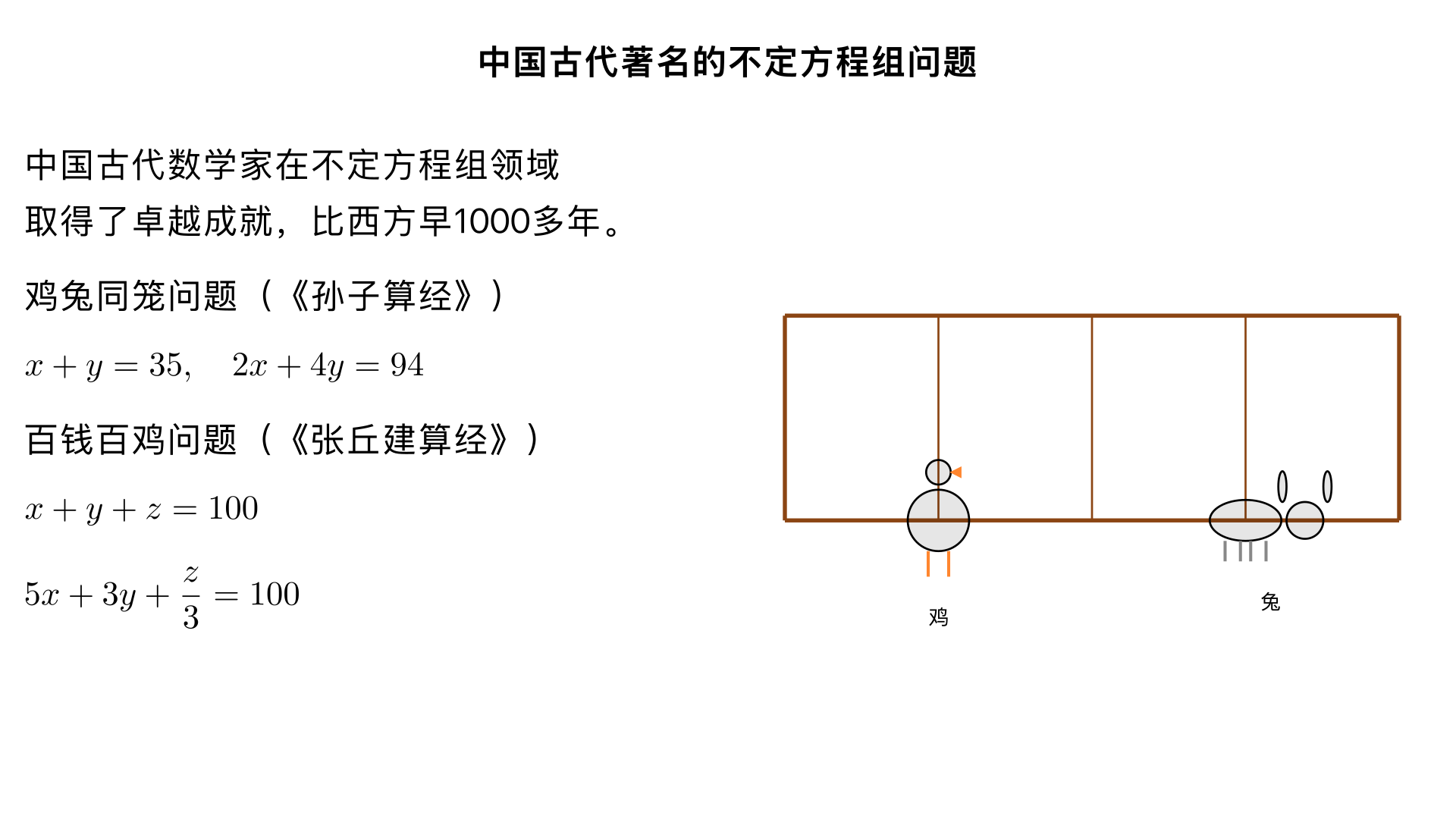
中国古代著名的一次不定方程组问题 一、鸡兔同笼问题(《孙子算经》) 原题:"今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?"(约公元 5 世纪) 题意:鸡兔同笼,共有 35 个头,94 只脚,求鸡兔各多少只。 1. 古代解法:除减法(抬脚法) 将脚数除以 2:94÷2=47 用 47 减去头数 35,得兔数:47-35=12 鸡数:35-12=23 原理:让每只鸡单脚站立(剩 1 脚),每只兔双脚站立(剩 2 脚)。此时脚数 47 比头数 35 多出的 12 即为兔子数(每只兔多 1 脚)。 2. 现代解法:二元一次方程组 设鸡 x 只,兔 y 只: plaintext x + y = 35 (头数) 2x + 4y = 94 (脚数) 解法: 由第一式得:x = 35 - y 代入第二式:2 (35-y) + 4y = 94 → 70 - 2y + 4y = 94 → 2y = 24 → y = 12 则 x = 35 - 12 = 23 解:鸡 23 只,兔 12 只。 二、百钱百鸡问题(《张丘建算经》) 原题:"今有鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一。凡百钱买鸡百只。问鸡翁母雏各几何。"(约公元 5-6 世纪) 题意:公鸡每只 5 钱,母鸡每只 3 钱,小鸡 3 只 1 钱,用 100 钱买 100 只鸡,求三种鸡各多少只。 1. 数学模型 设公鸡 x 只,母鸡 y 只,小鸡 z 只: plaintext x + y + z = 100 (总只数) 5x + 3y + z/3 = 100 (总钱数) 且 x,y,z 均为非负整数,z 是 3 的倍数。 2. 解法:消元法 由第一式得:z = 100 - x - y 代入第二式并化简:7x + 4y = 100 求此方程的非负整数解: 通解: 特解:x=0,y=25,则 z=75 通解公式:x=4t,y=25-7t,z=75+3t(t 为整数) 约束条件:x≥0,y≥0,z≥0 且 z 是 3 的倍数 得 t=0,1,2,3,对应四组解: 四组解: (0, 25, 75):0 只公鸡,25 只母鸡,75 只小鸡 (4, 18, 78):4 只公鸡,18 只母鸡,78 只小鸡 (8, 11, 81):8 只公鸡,11 只母鸡,81 只小鸡 (12, 4, 84):12 只公鸡,4 只母鸡,84 只小鸡 注:《张丘建算经》原书只给出前三组解,因当时无 "0" 的概念。 三、其他经典一次不定方程组问题 1. 五家共井问题(《九章算术》) 原题:五户人家共用一口井,各有井绳。甲家绳 2 条 + 乙家绳 1 条 = 井深;乙家绳 3 条 + 丙家绳 1 条 = 井深;丙家绳 4 条 + 丁家绳 1 条 = 井深;丁家绳 5 条 + 戊家绳 1 条 = 井深;戊家绳 6 条 + 甲家绳 1 条 = 井深。求各家绳长和井深。 数学模型(设各家绳长为 a,b,c,d,e,井深 h): plaintext 2a + b = h 3b + c = h 4c + d = h 5d + e = h 6e + a = h 特点:六元一次不定方程组(5 个方程,6 个未知数),有无数解,《九章算术》给出最小正整数解。 2. 物不知数问题(《孙子算经》,中国剩余定理原型) 原题:"今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?" 题意:一个数除以 3 余 2,除以 5 余 3,除以 7 余 2,求这个数。 解法(宋代秦九韶 "大衍求一术"): 构造三个数: 70(被 5、7 整除,除以 3 余 1) 21(被 3、7 整除,除以 5 余 1) 15(被 3、5 整除,除以 7 余 1) 解:N = 70×2 + 21×3 + 15×2 - 2×105 = 23 通解:N = 23 + 105k(k 为非负整数),最小正整数解为 23。 四、中国古代一次不定方程组问题的历史价值 开创数学新领域:《张丘建算经》的 "百鸡问题" 是世界上最早关于不定方程组的完整表述,比印度早 400 多年,比西方早 1000 多年。 算法创新: 《九章算术》的 "方程术"(直除法)是现代矩阵消元法的雏形 秦九韶的 "大衍求一术" 解决了一次同余方程组问题,被称为 "中国剩余定理" 数学思想: 体现了 "化繁为简" 的转化思想(如鸡兔同笼的抬脚法) 展示了 "枚举 - 验证" 的解题策略(百钱百鸡的多解求解) 反映了中国古代数学注重实用性的特点 五、一次不定方程组的现代应用 数学教育:作为培养方程思维的经典例题,帮助理解 "多元变量" 和 "约束条件" 概念 计算机算法: 枚举法→计算机暴力搜索 消元法→线性方程组求解程序 同余问题→密码学中的 RSA 算法基础 实际问题建模: 资源分配(如生产计划安排) 组合优化(如采购方案设计) 数字游戏和谜题设计 总结 中国古代一次不定方程组问题(鸡兔同笼、百钱百鸡等)不仅展示了古人的数学智慧,也为现代数学教育和应用提供了丰富素材。这些问题的解决思路(消元法、枚举法、同余理论等)与现代二元一次方程组解法一脉相承,体现了数学思想的永恒魅力。 思考:你能尝试用二元一次方程组解决 "鸡兔同笼" 的变式问题吗?如 "鸡与兔共有 100 只,鸡脚比兔脚多 80 只,求鸡兔各多少只?"

▶
七年级数学 / 二元一次方程组 / 中国古代数学的光辉成就 一、引言:古代中国的 "方程智慧" 中国是世界古代数学的发源地之一,早在两千多年前,我国古代数学家就已经系统研究了多元一次方程组的解法,其成果被收录在经典数学著作中,不仅是中国数学的瑰宝,也对世界数学发展产生了深远影响。在七年级学习的二元一次方程组,其核心思想和解法就可以追溯到中国古代的 "方程术",体现了古人卓越的逻辑思维和解题智慧。 二、核心成就:《九章算术》中的 "方程术" 1. 著作背景 《九章算术》是中国古代最重要的数学专著之一,成书于东汉时期(约公元 1 世纪),汇总了战国至秦汉时期的数学成果。书中第九章专门名为 "方程",这是世界数学史上最早对多元一次方程组进行系统论述的篇章,其中的 "方程术" 就是求解二元、三元甚至四元一次方程组的方法。 2. "方程" 的含义 古代的 "方程" 与现代的 "方程" 概念略有不同:古人将若干个含未知数的等式并列,用算筹(古代计算工具)摆出它们的系数和常数项,形成一个矩形的 "算筹方阵",这就是 "方程" 的本意。例如,求解二元一次方程组时,古人会用算筹分别表示两个方程的系数和常数项,再通过特定步骤消元求解。 3. 核心解法:"直除法"(古代版 "加减消元法") 《九章算术》中求解二元一次方程组的核心方法是 "直除法",其原理与现代的 "加减消元法" 完全一致,步骤如下: 第一步:将两个方程的系数和常数项用算筹按固定顺序排列(竖排,未知数系数在前,常数项在后); 第二步:通过 "直除"(即连续相减)的方式,消去其中一个未知数的系数,将二元一次方程组转化为一元一次方程; 第三步:求解一元一次方程,再代入原方程求出另一个未知数。 示例:《九章算术》中的经典问题(改编为现代二元一次方程组) 问题:今有上禾三秉("秉" 是古代容量单位),中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗。问上、中、下禾一秉各几何?(此为三元一次方程组,简化为二元示例如下) 简化二元问题:今有上禾 3 秉,下禾 1 秉,实 39 斗;上禾 2 秉,下禾 1 秉,实 34 斗。问上禾、下禾一秉各几斗? 现代解法:设上禾一秉 x 斗,下禾一秉 y 斗,列方程组: plaintext 3x + y = 39 ① 2x + y = 34 ② ① - ②得:x = 5,代入②得 y = 24,即上禾一秉 5 斗,下禾一秉 24 斗。 古代 "直除法":用算筹摆出两个方程的系数(上禾系数、下禾系数、常数项):第一行(算筹):3 1 39第二行(算筹):2 1 34用第一行连续减去第二行("直除"),直到第一行第一个系数变为 1:第一行 - 第二行:1 0 5(即 x = 5)再将 x = 5 代入第二行,求得 y = 24,与现代解法结果一致。 4. 历史地位 《九章算术》的 "方程术" 是世界数学史上最早的多元一次方程组系统解法,比西方同类成果早了一千多年(西方直到 17 世纪才由法国数学家笛卡尔系统提出线性方程组的解法)。这一成就充分体现了中国古代数学的实用性和逻辑性,是中国古代科技文明的重要标志。 三、其他古代经典问题(二元一次方程组应用) 除了《九章算术》,中国古代还有许多著名的数学问题,本质上都是二元一次方程组的应用,至今仍被收录在初中数学教材中: 1. 鸡兔同笼(出自《孙子算经》) 问题:今有雉(鸡)兔同笼,上有三十五头,下有九十四足。问雉兔各几何? 现代解法:设鸡 x 只,兔 y 只,列方程组: plaintext x + y = 35 (头数之和) 2x + 4y = 94 (足数之和) 用加减消元法解得:x = 23,y = 12,即鸡 23 只,兔 12 只。 古代解法:采用 "抬腿法"(本质是消元思想),让鸡和兔各抬起一半的足,此时足数为 47,头数仍为 35,足数 - 头数 = 兔的只数(47 - 35 = 12),再求鸡的只数。 2. 牛羊直金(出自《九章算术》) 问题:今有牛五、羊二,直金十两;牛二、羊五,直金八两。问牛、羊各直金几何? 现代解法:设牛直金 x 两,羊直金 y 两,列方程组: plaintext 5x + 2y = 10 ① 2x + 5y = 8 ② ①×2 得:10x + 4y = 20 ③;②×5 得:10x + 25y = 40 ④;④ - ③得:21y = 20,y = 20/21,代入①得 x = 34/21。 古代 "直除法":通过算筹排列系数,先消去 x 的系数(5 和 2 的最小公倍数 10),再求解 y,步骤与现代加减消元法一致。 四、古代数学成就的现代意义 1. 数学思想的传承 中国古代的 "方程术" 和消元思想,是现代线性代数的基础。七年级学习的二元一次方程组解法,本质上是对古代 "直除法" 的传承和简化,让我们体会到数学知识的连续性和发展性。 2. 文化自信的培养 了解中国古代数学的光辉成就,能让我们感受到中华优秀传统文化的魅力,认识到中国古代科技的领先地位,增强文化自信和民族自豪感。 3. 解题思路的启发 古代数学家从实际问题出发,通过构建 "方程"(算筹方阵)解决问题的思路,启示我们:数学源于生活,解决数学问题要注重逻辑推理和方法创新,同时要学会将复杂问题转化为简单问题(如消元法将二元转化为一元)。 五、应试考点与常见题型 1. 考点梳理 结合古代数学问题列二元一次方程组; 对比古代 "直除法" 与现代加减消元法的异同; 理解《九章算术》中 "方程术" 的历史地位。 2. 典型例题 例题:《九章算术》中有一道题:"今有共买物,人出八,盈三;人出七,不足四。问人数、物价各几何?"(意思是:几个人一起买一件物品,每人出 8 钱,还多 3 钱;每人出 7 钱,还少 4 钱。问人数和物价各是多少?) 解:设人数为 x,物价为 y 钱,列方程组: plaintext 8x - y = 3 y - 7x = 4 两式相加得:x = 7,代入得 y = 53。 答:人数为 7 人,物价为 53 钱。 六、总结 中国古代数学在二元一次方程组领域的成就,以《九章算术》的 "方程术" 为代表,不仅开创了世界多元一次方程组解法的先河,更蕴含着 "消元转化"" 数形结合 " 的重要数学思想。这些成就不仅是历史的光辉,更是我们学习数学的宝贵资源 —— 通过了解古代数学问题,我们既能巩固二元一次方程组的知识,又能感受数学的文化底蕴,培养逻辑思维和创新意识。 正如古代数学家通过算筹摆出方程组的智慧,今天的我们也能通过数学知识解决生活中的问题,传承这份跨越千年的 "方程智慧"。

▶
详细讲述 解卦——雷雨作解:脱险之道与善后智慧 一、卦序逻辑:从艰难到缓解 1. 《序卦传》的必然转化 “蹇者,难也。物不可以终难,故受之以解。解者,缓也。” 蹇卦(水山蹇)象征艰难险阻 → 但事物不会永远处于艰难中 → 解卦(雷水解)象征缓解、解除 金景芳指出:这体现了《周易》“穷则变,变则通”的辩证思想 2. 蹇卦与解卦的综卦关系 蹇卦(䷦):上坎下艮,山上有水,险阻在前 解卦(䷧):上震下坎,雷雨作,百果草木皆甲坼(生机勃发) 二卦互为综卦(将蹇卦上下颠倒即得解卦),表明险难与解除是同一过程的不同阶段 二、解卦(雷水解)卦象的解放之象 1. “雷雨作”的生机勃发 基本卦象:上震雷,下坎水 → 雷雨大作,滋润万物 自然象征: 冬季(坎为水,为冬)过后,春雷(震为雷,为春)震动,雨水降临,冰消雪融 万物解除束缚,破壳而出(“百果草木皆甲坼”) 金景芳引申:此象喻示政治严苛(坎险)之后,仁政施行(震动),万民获得新生 2. 卦德分析与行动原则 下坎为险,上震为动 → 动而出险 《彖传》:“解,险以动,动而免乎险,解。” 核心智慧:在险境中积极行动,通过行动脱离险境 3. 爻位结构中的隐患 六三阴柔失正,上六无应 → 提示解难后可能产生新的问题 九二、九四阳刚有力,为解难主力 金景芳提醒:解卦不是一劳永逸,需防“致寇至” 三、彖传精解:解困之道 “解,险以动,动而免乎险,解。 解利西南,往得众也。 其来复吉,乃得中也。 有攸往夙吉,往有功也。 天地解而雷雨作,雷雨作而百果草木皆甲坼。 解之时大矣哉!” 1. “险以动,动而免乎险”的行动哲学 辩证关系:险境中行动(险以动),行动才能脱险(动而免乎险) 历史例证:刘邦被围荥阳,用陈平计突围(动),终免于险 反面教材:宋襄公“不鼓不成列”,坐失战机,未“动而免乎险” 2. “解利西南,往得众也”的民心指向 西南象征:坤方,平地,众庶(坤为众) “往得众”:前往西南可得民众支持 与蹇卦呼应:蹇卦“利西南”为避险,解卦“利西南”为得众 政治智慧:解难后需争取民心,如武王克商后“释箕子囚,封比干墓” 3. “其来复吉,乃得中也”的回归原则 “来复”:回归常态,恢复秩序 “得中”:符合中道(指九二居中) 政策启示:动乱平息后,应休养生息,恢复常规 历史例证:汉初萧何“与民休息”,是“其来复吉” 4. “有攸往夙吉,往有功也”的时效原则 “夙吉”:及早行动则吉(夙,早也) “往有功”:前往可建功业 战术要求:解决遗留问题要迅速,如周公东征速平管蔡之乱 5. “天地解而雷雨作…”的自然意象升华 将人事解脱与天地生化相联系 寓意:政治解困如雷雨滋润万物,带来生机 金景芳阐发:解卦蕴含“革命解放”的正当性,如汤武革命“顺乎天而应乎人” 6. “解之时大矣哉!”的赞叹 解卦的时义太重大了! 强调:把握解难时机的重要性,早则不及,迟则生变 四、大象传:“赦过宥罪”的宽恕精神 “雷雨作,解。君子以赦过宥罪。” 1. “赦过宥罪”的政治智慧 赦过:赦免无心过失 宥罪:宽恕有意罪过(但非免除惩罚,是减刑) 与《尚书》互证:“眚灾肆赦,怙终贼刑”(过失犯罪可赦,惯犯严惩) 2. 历史应用 汉文帝废肉刑:体现“宥罪”精神 唐太宗纵囚:风险之举,但收服人心 现代意义:战后和解、转型正义中的宽恕政策 3. 金景芳提醒:“赦过宥罪”不是无原则宽大,而是“解”后争取人心的策略 五、爻辞精析:解难的六个要点 解卦六爻侧重解难之后如何巩固成果、防止反复,是一套“善后指南”。 1. 初六:无咎。 简短爻辞,深意存焉:初六阴柔居解始,与九四正应 “无咎”条件:解难之初,低调顺从(上应九四),不争功,故无咎 象征:普通民众在解放后安分守己,可得无咎 历史情景:商民在周克商后,服从新朝,得保平安 2. 九二:田获三狐,得黄矢,贞吉。 “田获三狐”:田猎获得多只狐狸(狐象征小人、隐患) “得黄矢”:得到黄色箭矢(黄为中色,矢为直,象征中直之道) 爻象:九二阳刚居中,为解难主力 含义: 解难后需肃清余孽(三狐) 方法要中正(黄矢) 历史例证:周公诛管叔、放蔡叔、囚霍叔(三狐),但存中道(不滥杀) 3. 六三:负且乘,致寇至,贞吝。 全卦核心警示,源自孔子在《系辞传》中的重点阐发 生动画面: “负且乘”:背着财物坐在车上(小人得志,炫耀富贵) “致寇至”:招致强盗来抢 爻象:六三阴柔失正,居下卦之上,象征才德不配位的小人 孔子阐发(《系辞上》第八章): “作《易》者其知盗乎?…小人而乘君子之器,盗思夺之矣。” 揭示:德不配位,必招灾祸 现实意义:企业危机后,管理者若炫耀成功,可能引发新的危机 4. 九四:解而拇,朋至斯孚。 “解而拇”:解开你大脚趾的束缚(拇,足大趾,指初六) “朋至斯孚”:朋友到来,以诚信相待 爻象:九四阳居阴位,刚柔相济,下应初六 策略:解脱基层束缚(解而拇),则民众(朋)诚心归附(斯孚) 政策对应:汉高祖“约法三章”,解秦苛法,得关中民心 5. 六五:君子维有解,吉。有孚于小人。 “君子维有解”:君子被捆绑又得解脱(维,系也) “吉”:吉祥 “有孚于小人”:以诚信感化小人 爻象:六五柔中居尊,下应九二,处震卦中位 领袖之道: 自身曾受困(维),终得解 掌权后不报复,以诚信待小人(包括曾经的敌人) 历史典范:齐桓公不记管仲射钩之仇,任用为相,终成霸业 6. 上六:公用射隼于高墉之上,获之,无不利。 生动比喻: “公用射隼”:王公射杀凶鸟(隼,猛禽,象征残存的恶势力) “于高墉之上”:在高墙上(墉,城墙,象征险要位置) 爻象:上六处解之终,仍有隐患(隼)居高墉,需彻底清除 “获之,无不利”:擒获它,无所不利 历史例证:汉武帝彻底解决诸侯王问题(推恩令),巩固统一 金景芳总结:解卦以“射隼”作结,强调解难的彻底性 六、解卦的解难智慧总论 1. 行动原则:“险以动,动而免乎险” 积极行动,脱出险境 2. 政治方向:“利西南,往得众” 解难后争取民心,稳定大局 3. 善后要务: 肃清余孽(田获三狐) 防止炫耀(负且乘) 解脱民困(解而拇) 感化小人(有孚于小人) 清除顽敌(射隼高墉) 4. 宽恕精神:“赦过宥罪” 但宽恕有度,不是无限赦免 5. 金景芳总结:解卦是儒家“拨乱反正”思想的体现,强调解难要彻底,善后要谨慎,治国要以德服人。
▶
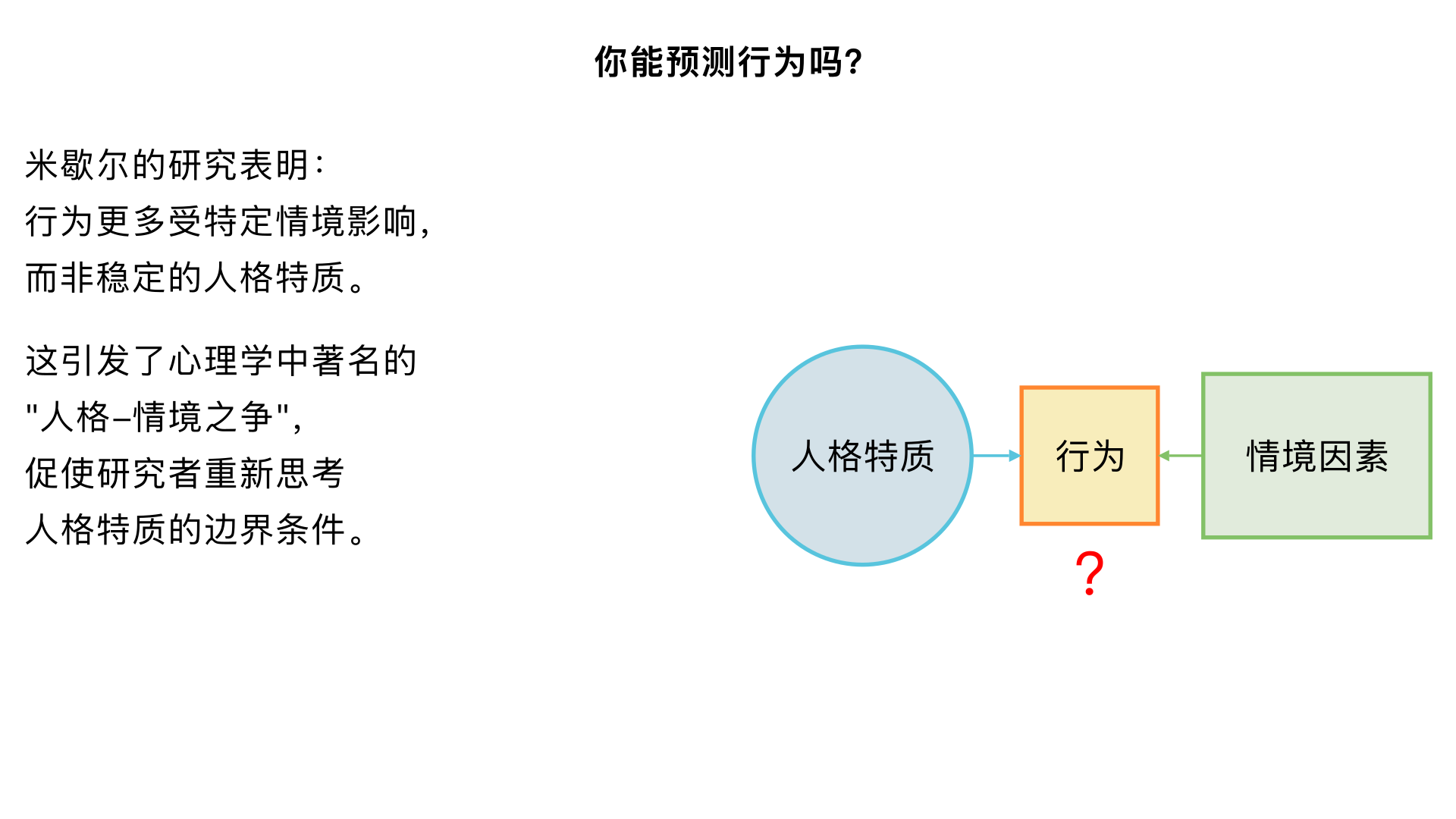
你能预测行为吗? (米歇尔的“人格与情境”之争) 主要内容:通过对大量研究的回顾,提出行为更多地受到特定情境的影响,而非稳定的人格特质。这一观点引发了人格心理学中著名的“人-情境之争”,促使研究者更深入地思考特质的边界条件。
▶
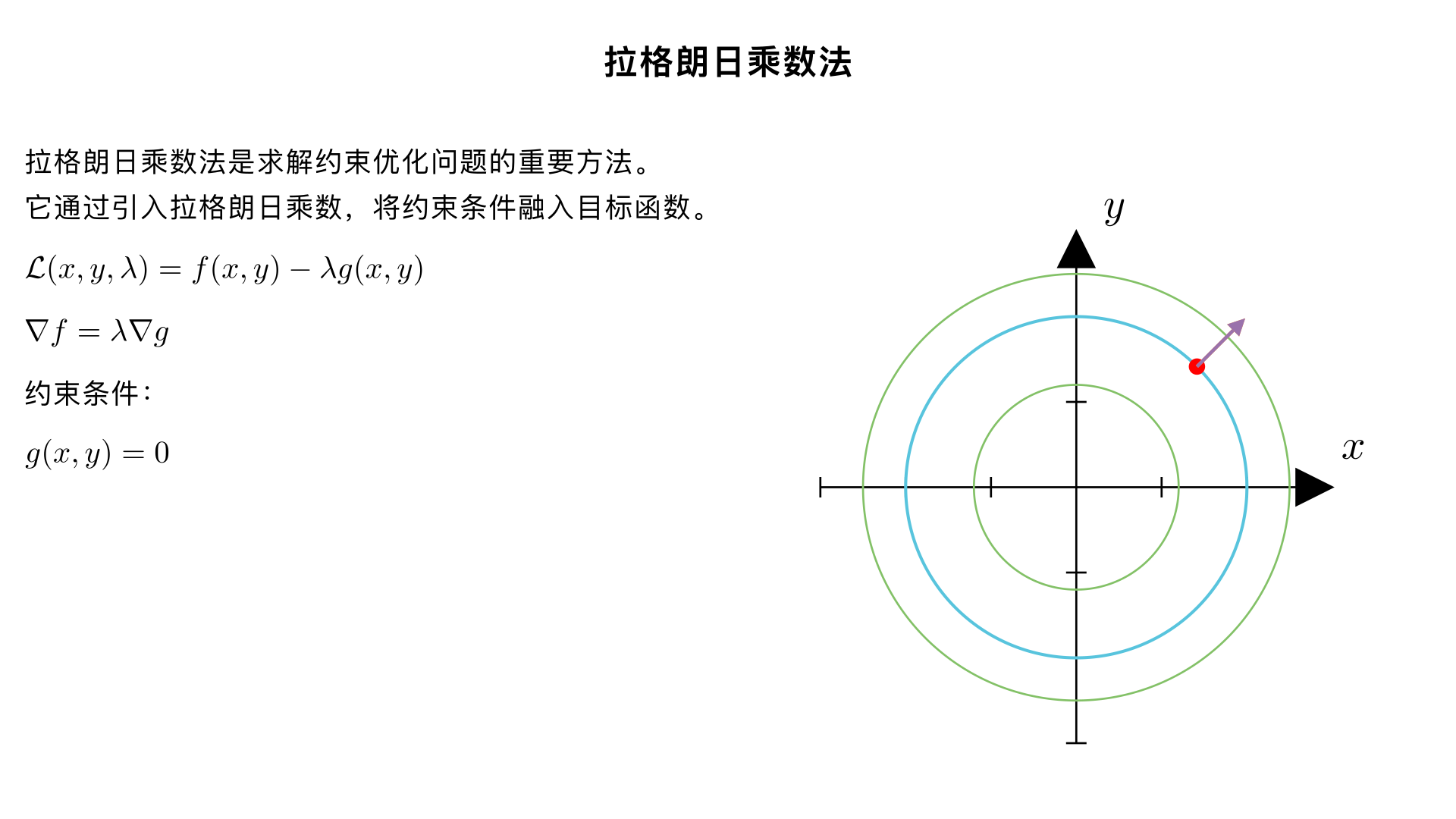
解释拉格朗日乘数法

▶
解释拉格朗日乘数法
▶
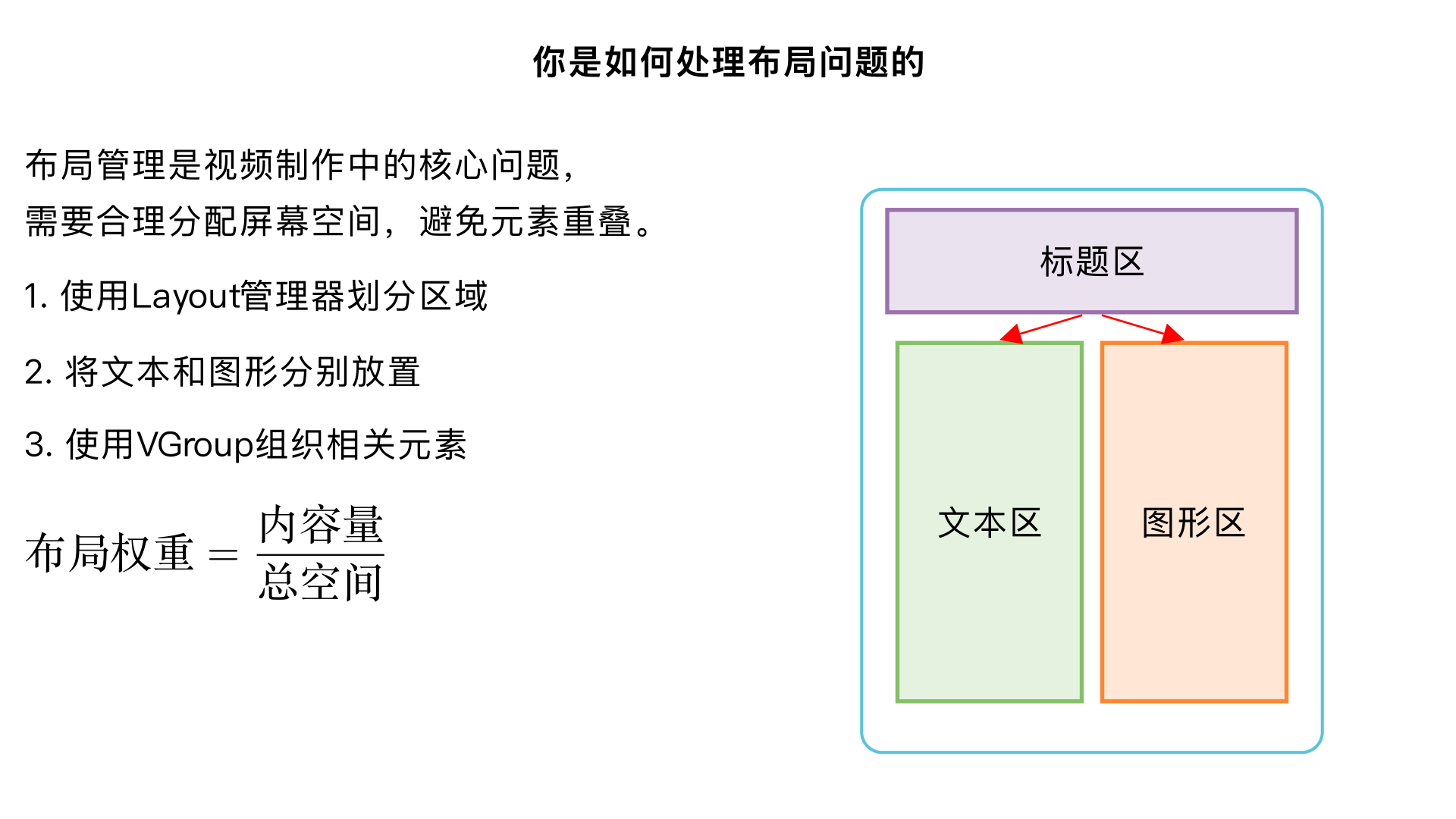
你是如何处理布局问题的
▶
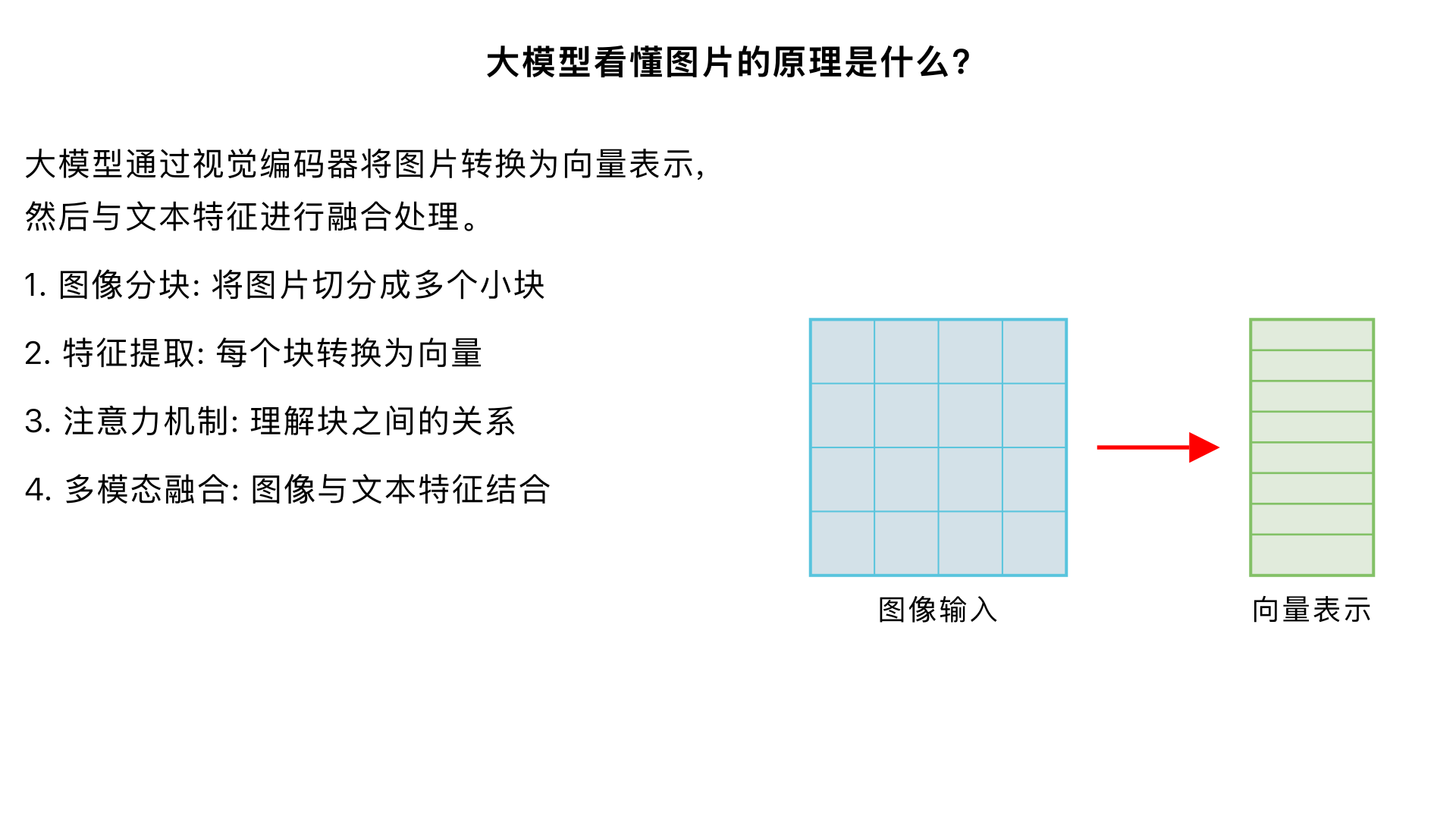
大模型看懂图片的原理是什么?

▶
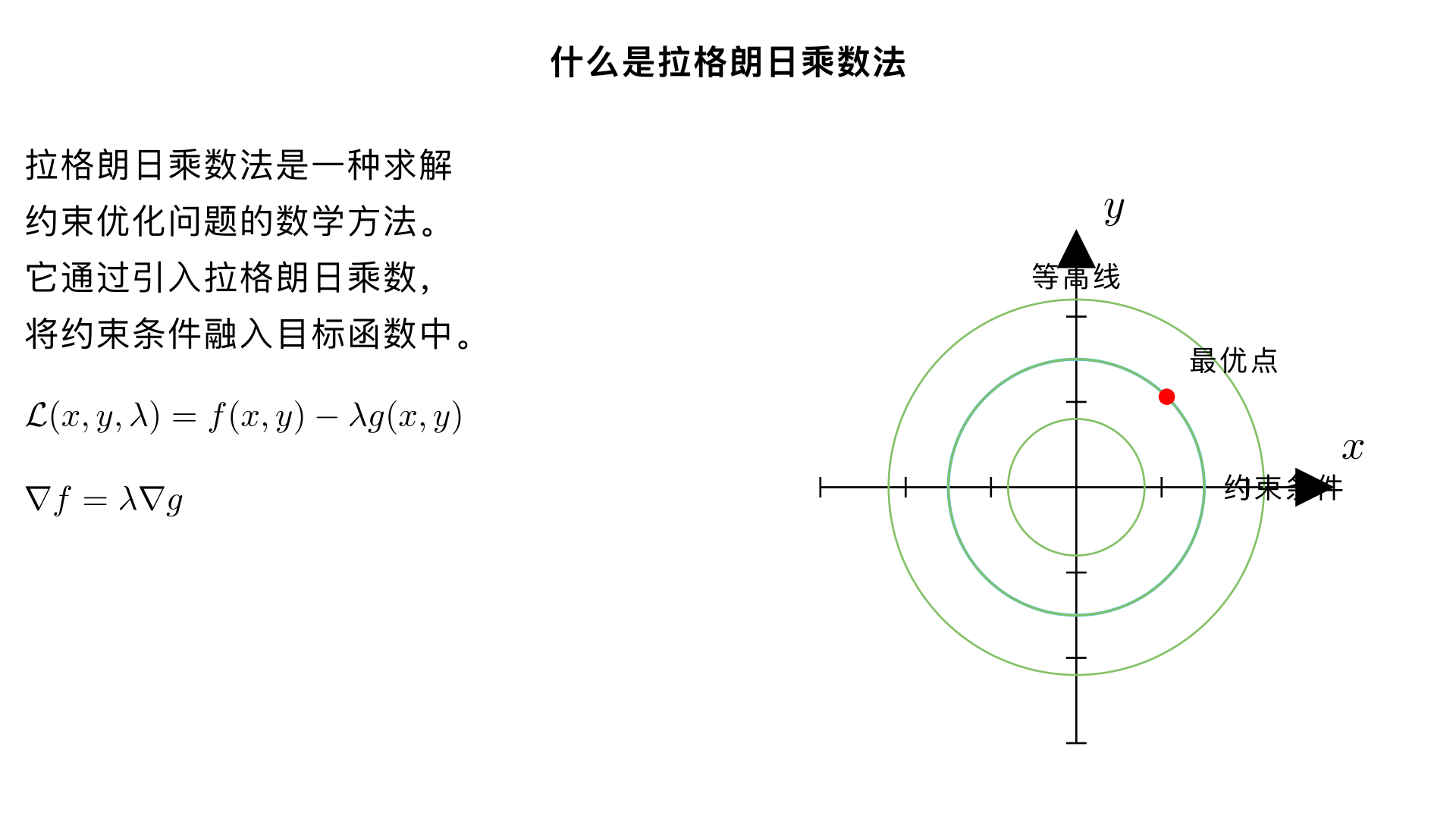
解释拉格朗日乘数法
▶