T
Teach Me AnythingTMA
Video History
Page 30 / 43![**Discuss the continuity of the function**
[
f(x, y, z) = \frac{61}{\sqrt{x^2 + y^2 + z^2}}
]
**Options:**
* ○ continuous everywhere
* ○ continuous except where (x^2 + y^2 + z^2 < 1)
* ○ continuous except where (x^2 + y^2 + z^2 > 1)
* ○ continuous except where (x^2 + y^2 + z^2 > 0)
* ○ continuous except at ((0, 0, 0))](https://manimvideo.explanation.fun/video/cover/578588523731120129.png)
▶
**Discuss the continuity of the function** [ f(x, y, z) = \frac{61}{\sqrt{x^2 + y^2 + z^2}} ] **Options:** * ○ continuous everywhere * ○ continuous except where (x^2 + y^2 + z^2 < 1) * ○ continuous except where (x^2 + y^2 + z^2 > 1) * ○ continuous except where (x^2 + y^2 + z^2 > 0) * ○ continuous except at ((0, 0, 0))

▶
Match the graph of the surface with one of the contour maps. f(x, y) = e^(1 − x^2 + y^2)

▶
10:占卜的后续步骤——变卦与解卦主要内容:根据三个数字确定“本卦”、“互卦”和“变卦”。确定“动爻”(变爻)的位置。 解卦的核心:以本卦的卦辞和变爻的爻辞为主,互卦和变卦为辅。

▶
第10课:占卜的后续步骤——变卦与解卦 主要内容: 如何根据三个数字确定“本卦”、“互卦”和“变卦”。 确定“动爻”(变爻)的位置。 解卦的核心:以本卦的卦辞和变爻的爻辞为主,互卦和变卦为辅。

▶
Home 9:《易经》的运用——占卜的原则与方法 主要内容: 占卜的哲学基础:“寂然不动,感而遂通”。 占卜的三原则:不诚不占、不义不占、不疑不占。 介绍傅佩荣老师推荐的“数字占卜法”(简单、易行、无需道具)。

▶
第5课、所见即所学? (哈伯和托伦的“感觉剥夺与图形识别”研究) 主要内容:让被试长时间佩戴特制的 distorting 眼镜,发现其知觉逐渐适应并恢复正常。但当摘掉眼镜后,其知觉又需要重新适应。这证明知觉不仅由感觉输入决定,更深受过去经验和学习的影响。
![Here’s the full markdown version of your provided images:
---
### (a) Adjacency List Representation
**Graph:**
Vertices: a, b, c, d
**Adjacency List:**
| Vertex | Adjacent Vertices |
| :----: | :---------------: |
| a | c |
| b | d |
| c | b, d |
| d | b |
---
### (b) Adjacency Matrix Representation
**Graph:**
Vertices: a, b, c, d
**Adjacency Matrix:**
[
M_b =
\begin{pmatrix}
& a & b & c & d \
a & 0 & 1 & 0 & 1 \
b & 1 & 0 & 1 & 1 \
c & 0 & 1 & 0 & 1 \
d & 1 & 1 & 1 & 0
\end{pmatrix}
]
---
### (c) Adjacency Matrix Representation
**Graph:**
Vertices: a, b, c, d
**Adjacency Matrix:**
[
M_c =
\begin{pmatrix}
& a & b & c & d \
a & 1 & 0 & 1 & 1 \
b & 0 & 1 & 0 & 1 \
c & 1 & 1 & 1 & 0 \
d & 0 & 1 & 0 & 1
\end{pmatrix}
]
---
注意使用 mathtex 显示公式
中文输出](https://manimvideo.explanation.fun/video/cover/578443240306839553.png)
▶
Here’s the full markdown version of your provided images: --- ### (a) Adjacency List Representation **Graph:** Vertices: a, b, c, d **Adjacency List:** | Vertex | Adjacent Vertices | | :----: | :---------------: | | a | c | | b | d | | c | b, d | | d | b | --- ### (b) Adjacency Matrix Representation **Graph:** Vertices: a, b, c, d **Adjacency Matrix:** [ M_b = \begin{pmatrix} & a & b & c & d \ a & 0 & 1 & 0 & 1 \ b & 1 & 0 & 1 & 1 \ c & 0 & 1 & 0 & 1 \ d & 1 & 1 & 1 & 0 \end{pmatrix} ] --- ### (c) Adjacency Matrix Representation **Graph:** Vertices: a, b, c, d **Adjacency Matrix:** [ M_c = \begin{pmatrix} & a & b & c & d \ a & 1 & 0 & 1 & 1 \ b & 0 & 1 & 0 & 1 \ c & 1 & 1 & 1 & 0 \ d & 0 & 1 & 0 & 1 \end{pmatrix} ] --- 注意使用 mathtex 显示公式 中文输出
![### 5. Verify that the following program segment is correct with respect to the initial assertion *T* and the final assertion: [ (x \le y \land \text{max} = y) \lor (x > y \land \text{max} = x) ] ```plaintext if x <= y then max := y else max := x ``` --- **Solution:** Initial assertion *T* means this segment will always run and everything is always correct at the beginning of the segment. If ( x < y ) initially, *max* is set equal to *y*, so the left side of the final assertion ∨: ((x \le y \land \text{max} = y)) is true. If ( x = y ) initially, *max* is set equal to *y*, so ((x \le y \land \text{max} = y)) is again true. If ( x > y ), *max* is set equal to *x*, so the right side of the final assertion ∨: ((x > y \land \text{max} = x)) is true. Since ∨ is true whenever one or the other or both sides are true, the final assertion is always true and the program segment is correct. 注意使用 mathtex 显示公式
中文解题](https://manimvideo.explanation.fun/video/cover/578435076945432577.png)
▶
### 5. Verify that the following program segment is correct with respect to the initial assertion *T* and the final assertion: [ (x \le y \land \text{max} = y) \lor (x > y \land \text{max} = x) ] ```plaintext if x <= y then max := y else max := x ``` --- **Solution:** Initial assertion *T* means this segment will always run and everything is always correct at the beginning of the segment. If ( x < y ) initially, *max* is set equal to *y*, so the left side of the final assertion ∨: ((x \le y \land \text{max} = y)) is true. If ( x = y ) initially, *max* is set equal to *y*, so ((x \le y \land \text{max} = y)) is again true. If ( x > y ), *max* is set equal to *x*, so the right side of the final assertion ∨: ((x > y \land \text{max} = x)) is true. Since ∨ is true whenever one or the other or both sides are true, the final assertion is always true and the program segment is correct. 注意使用 mathtex 显示公式 中文解题
![### 5. Verify that the following program segment is correct with respect to the initial assertion *T* and the final assertion:
[
(x \le y \land \text{max} = y) \lor (x > y \land \text{max} = x)
]
```plaintext
if x <= y then
max := y
else
max := x
```
---
**Solution:**
Initial assertion *T* means this segment will always run and everything is always correct at the beginning of the segment.
If ( x < y ) initially, *max* is set equal to *y*, so the left side of the final assertion ∨:
((x \le y \land \text{max} = y)) is true.
If ( x = y ) initially, *max* is set equal to *y*, so ((x \le y \land \text{max} = y)) is again true.
If ( x > y ), *max* is set equal to *x*, so the right side of the final assertion ∨:
((x > y \land \text{max} = x)) is true.
Since ∨ is true whenever one or the other or both sides are true, the final assertion is always true and the program segment is correct.
注意使用 mathtex 显示公式](https://manimvideo.explanation.fun/video/cover/578434488337780737.png)
▶
### 5. Verify that the following program segment is correct with respect to the initial assertion *T* and the final assertion: [ (x \le y \land \text{max} = y) \lor (x > y \land \text{max} = x) ] ```plaintext if x <= y then max := y else max := x ``` --- **Solution:** Initial assertion *T* means this segment will always run and everything is always correct at the beginning of the segment. If ( x < y ) initially, *max* is set equal to *y*, so the left side of the final assertion ∨: ((x \le y \land \text{max} = y)) is true. If ( x = y ) initially, *max* is set equal to *y*, so ((x \le y \land \text{max} = y)) is again true. If ( x > y ), *max* is set equal to *x*, so the right side of the final assertion ∨: ((x > y \land \text{max} = x)) is true. Since ∨ is true whenever one or the other or both sides are true, the final assertion is always true and the program segment is correct. 注意使用 mathtex 显示公式

▶
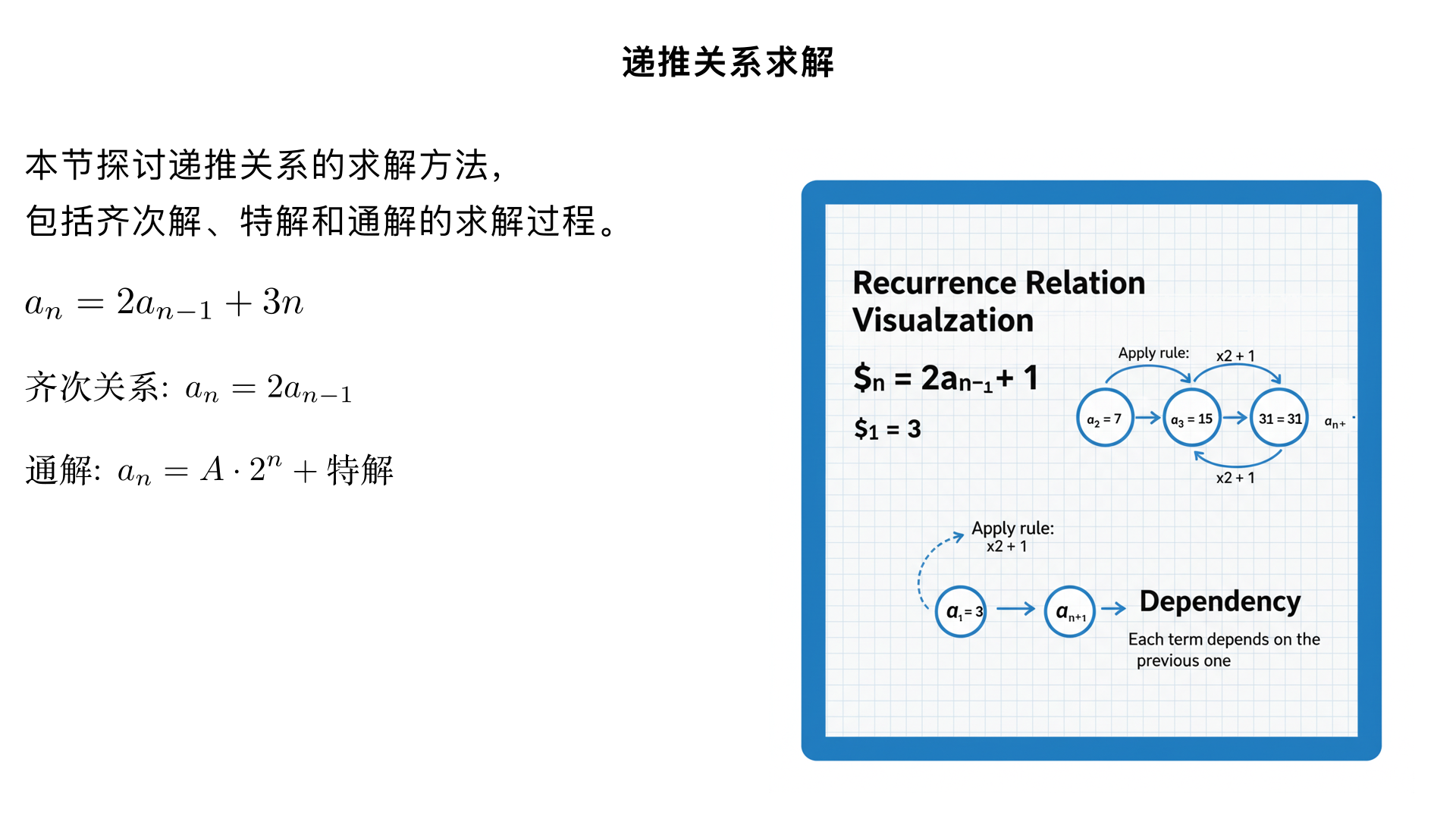
Set up a generating function and use it to find the number of ways in which nine identical blocks can be given to four children if each child gets at least one block.
![3. Solve the recurrence relation
\[
a_n = 2a_{n-1}
\]
using generating functions. Where \( a_0 = 1 \)
*Note:* *I won’t ask a harder one than this if specifically requesting generating functions to solve a recurrence.*
注意公式使用 mathtex](https://manimvideo.explanation.fun/video/cover/578398786136838145.png)
▶
3. Solve the recurrence relation \[ a_n = 2a_{n-1} \] using generating functions. Where \( a_0 = 1 \) *Note:* *I won’t ask a harder one than this if specifically requesting generating functions to solve a recurrence.* 注意公式使用 mathtex
▶