T
Teach Me AnythingTMA
Video History
Page 26 / 43
▶
感谢记忆! (奈瑟的“自传体记忆”研究) 主要内容:研究了人们对个人生活中重大事件的记忆(“闪光灯记忆”),发现尽管当事人对这类记忆的信心很高,但它们同样会随着时间推移而扭曲和遗忘,并非我们想象的那么精确。
▶
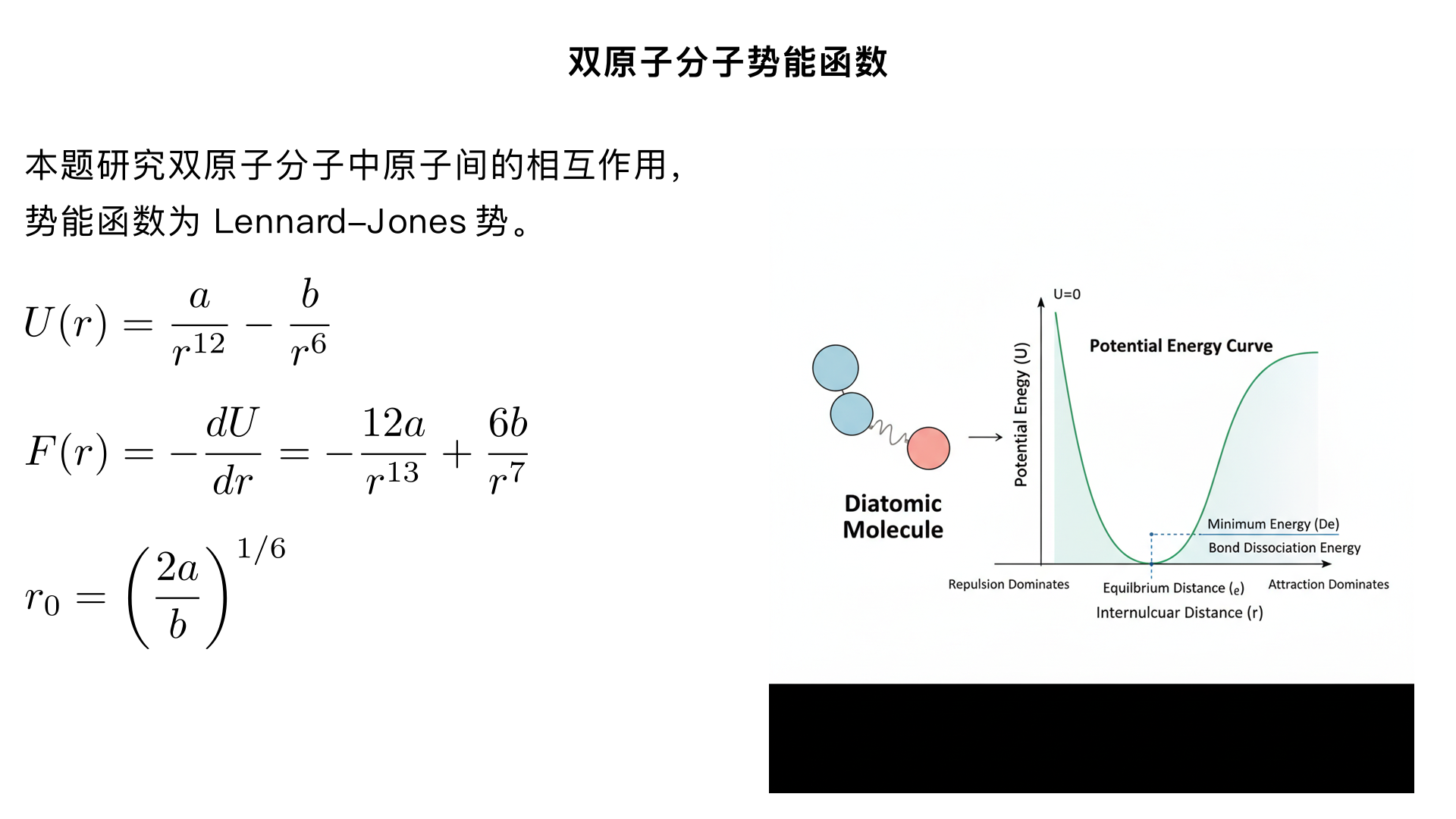
7. (15 pts) The potential energy function for either one of the two atoms in a diatomic molecule can be approximated by \(U(r) = a / r^{12} - b / r^{6}\) , where \(a\) and \(b\) are constants and \(r\) is the distance between the atoms. (a) Derive an expression for the force on an atom as a function of \(r\) , \(a\) , and \(b\) . (b) At what distance \(r\) does the potential energy have a local minimum (not at \(r = \infty\) )? (c) What is the force on the atom for this value of \(r\) ? 讲题 解题
▶
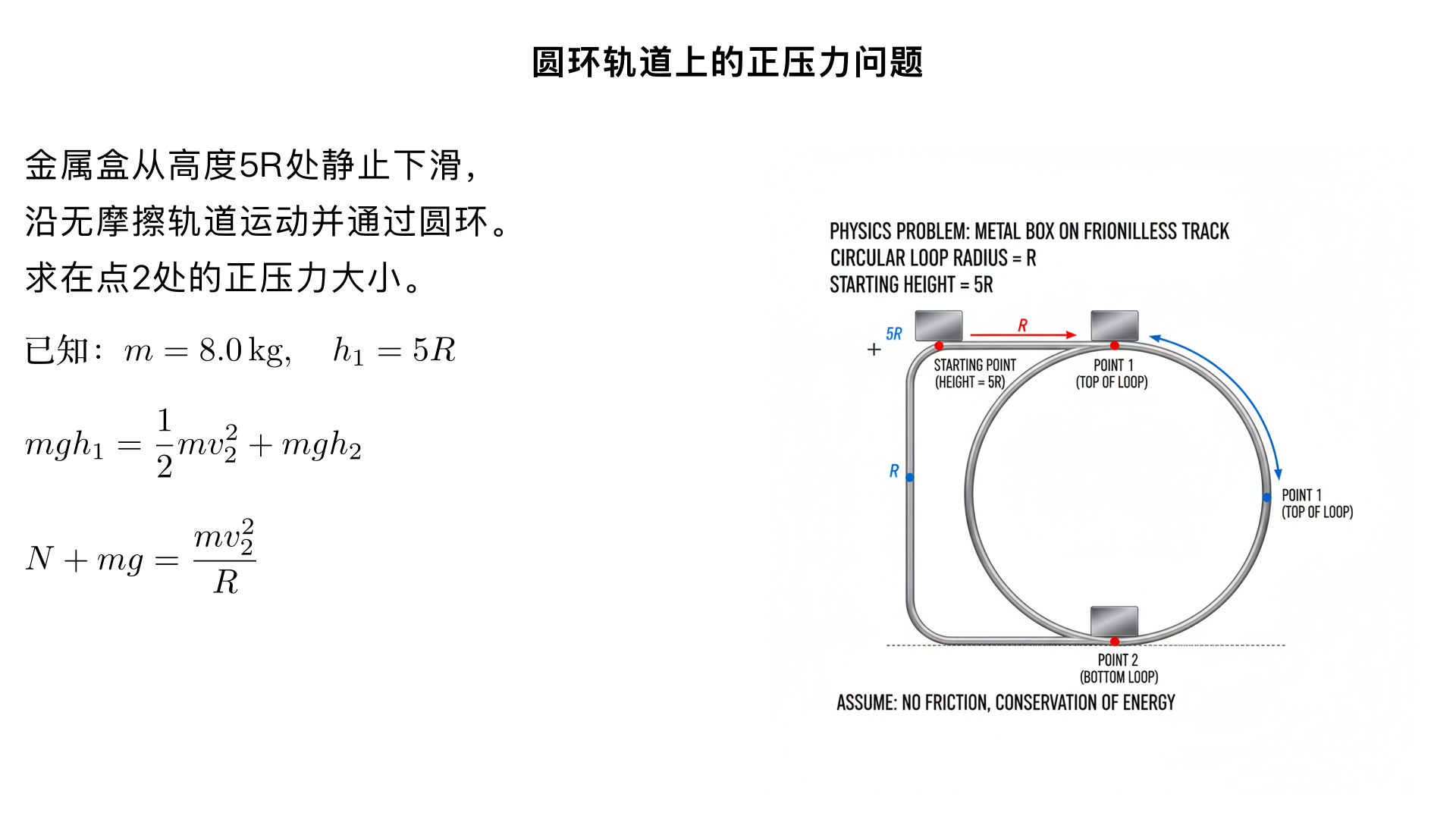
6. (12 pts) A metallic box begins at rest at point 1 at a height of \(5R\) , where \(R\) is the radius of the circular part of the track. The box slides down the frictionless track and around the loop. If the box has a mass of \(8.0 \mathrm{kg}\) , what is the magnitude of the normal force acting on the box at point 2? 讲题 解题
▶
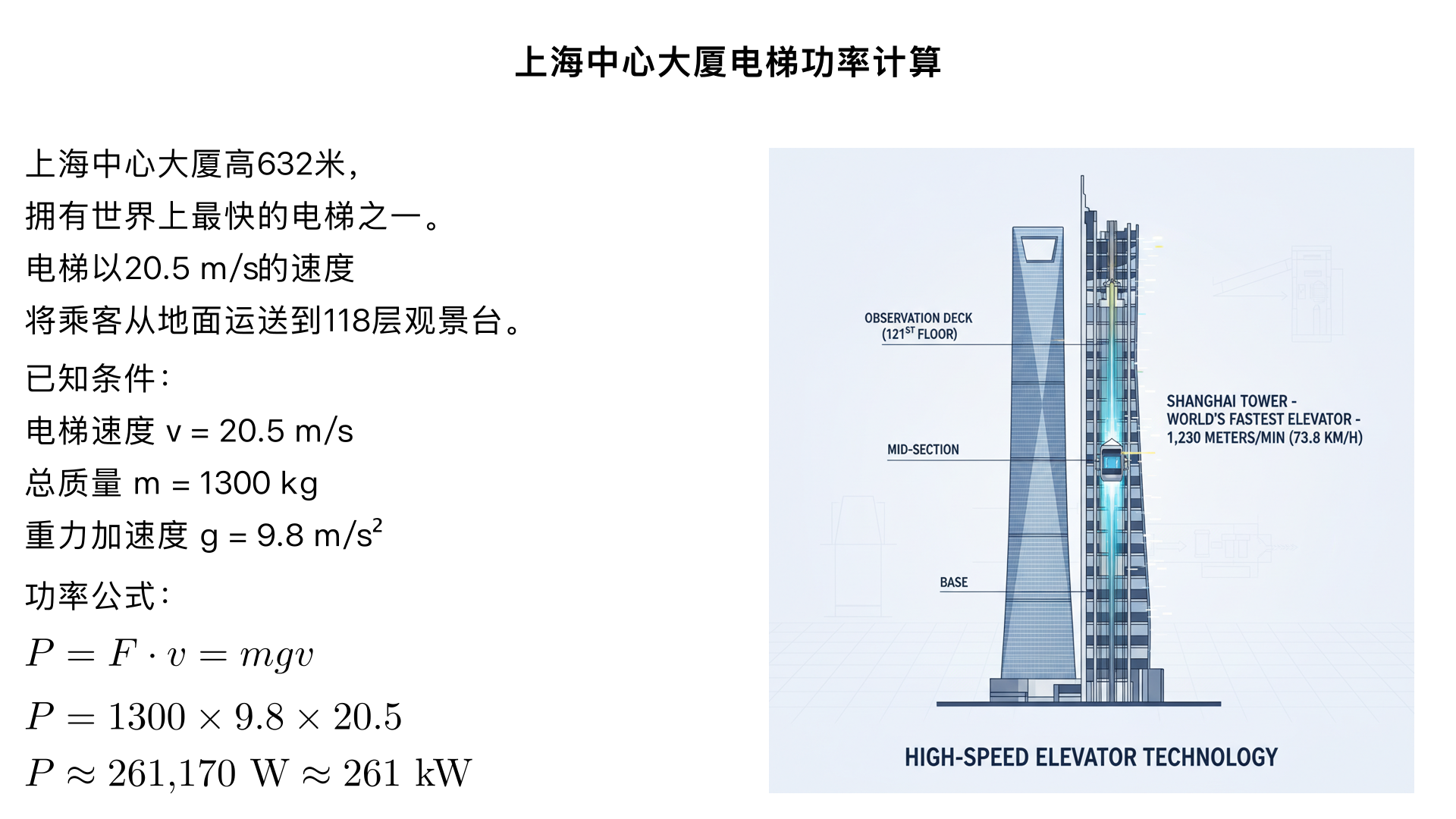
5. (12 pts) The Shanghai Tower in China is a skyscraper measuring 632 meters high. It is home to one of the world's fastest elevators. The elevators transport visitors from the ground floor to the observation deck on the 118th floor at speeds up to 20.5 m/s. Determine the power delivered by the motor to lift 10 passengers at this (constant) speed. Assume that the combined mass of the passengers and elevator cabin is 1300 kg. 讲题 解题
![4. (18 pts) A 1.0 kg particle is released from rest at the origin \(\vec{\mathbf{r}}_{0} = (0 \hat{\mathbf{i}} + 0 \hat{\mathbf{j}}) \mathrm{m}\) , and is then subject to a position-dependent force given in Newtons by \[\vec{\mathbf{F}} (x,y) = (y \hat{\mathbf{i}} -x \hat{\mathbf{j}}).\] Furthermore, the particle is constrained to a parabolic curve so that it only moves along the path \[y = 10x - x^{2}\] where both \(x\) and \(y\) are measured in meters. (a) Is this force conservative? How can you tell? (b) Calculate the work done by the force on the particle as it moves along the parabolic path to a final position \(\vec{\mathbf{r}}_{f} = (10 \hat{\mathbf{i}} + 0 \hat{\mathbf{j}}) \mathrm{m}\) . (c) What is the speed of the particle after this displacement? 解题 讲题 注意 使用 MathTex 显示公式](https://manimvideo.explanation.fun/video/cover/581332909771198465.png)
▶
4. (18 pts) A 1.0 kg particle is released from rest at the origin \(\vec{\mathbf{r}}_{0} = (0 \hat{\mathbf{i}} + 0 \hat{\mathbf{j}}) \mathrm{m}\) , and is then subject to a position-dependent force given in Newtons by \[\vec{\mathbf{F}} (x,y) = (y \hat{\mathbf{i}} -x \hat{\mathbf{j}}).\] Furthermore, the particle is constrained to a parabolic curve so that it only moves along the path \[y = 10x - x^{2}\] where both \(x\) and \(y\) are measured in meters. (a) Is this force conservative? How can you tell? (b) Calculate the work done by the force on the particle as it moves along the parabolic path to a final position \(\vec{\mathbf{r}}_{f} = (10 \hat{\mathbf{i}} + 0 \hat{\mathbf{j}}) \mathrm{m}\) . (c) What is the speed of the particle after this displacement? 解题 讲题 注意 使用 MathTex 显示公式

▶
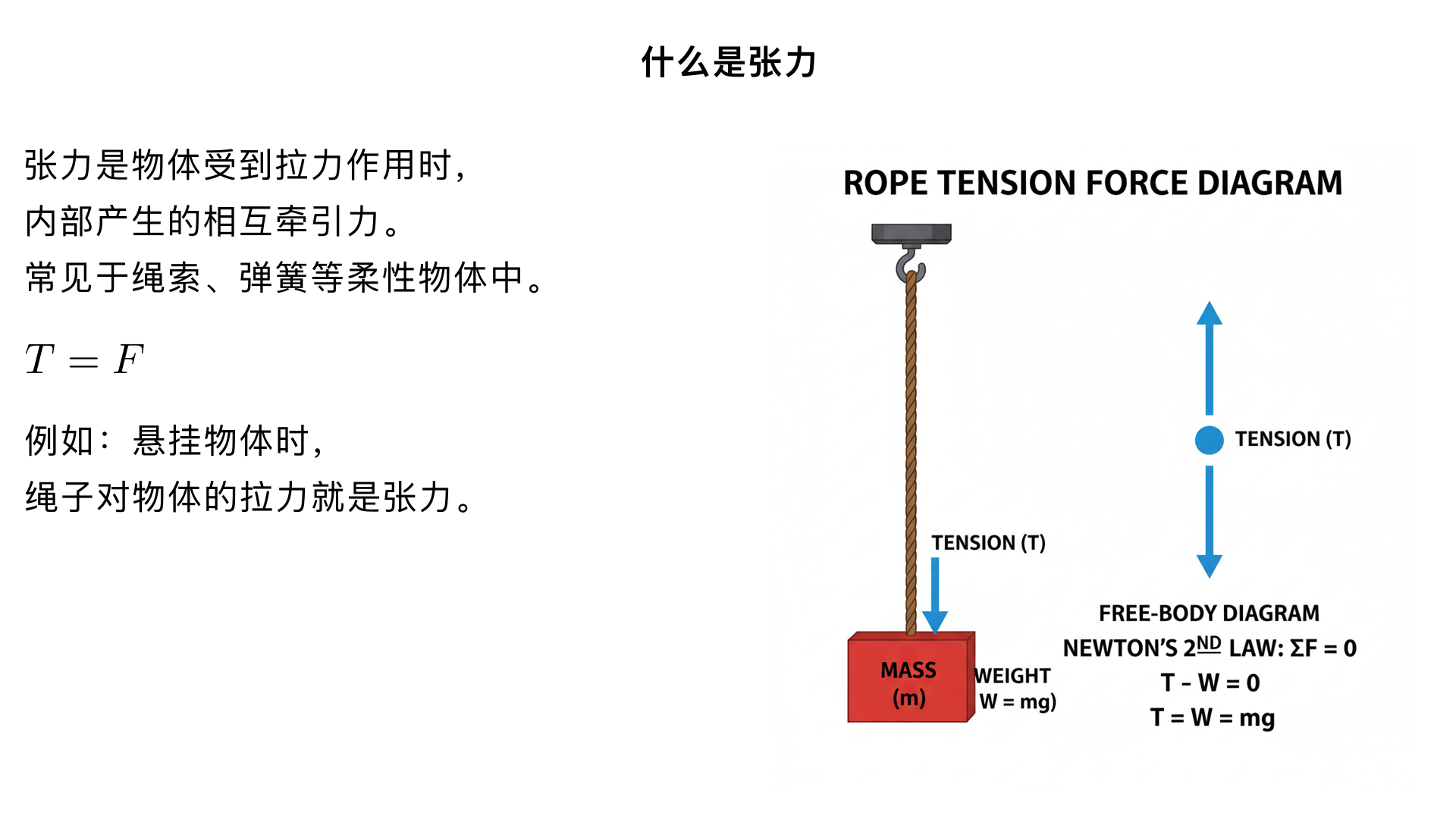
什么是保守力
▶
4. (18 pts) A 1.0 kg particle is released from rest at the origin \(\vec{\mathbf{r}}_{0} = (0 \hat{\mathbf{i}} + 0 \hat{\mathbf{j}}) \mathrm{m}\) , and is then subject to a position-dependent force given in Newtons by \[\vec{\mathbf{F}} (x,y) = (y \hat{\mathbf{i}} -x \hat{\mathbf{j}}).\] Furthermore, the particle is constrained to a parabolic curve so that it only moves along the path \[y = 10x - x^{2}\] where both \(x\) and \(y\) are measured in meters. (a) Is this force conservative? How can you tell? (b) Calculate the work done by the force on the particle as it moves along the parabolic path to a final position \(\vec{\mathbf{r}}_{f} = (10 \hat{\mathbf{i}} + 0 \hat{\mathbf{j}}) \mathrm{m}\) . (c) What is the speed of the particle after this displacement? 解题 讲题 使用 MathTex 显示公式
▶
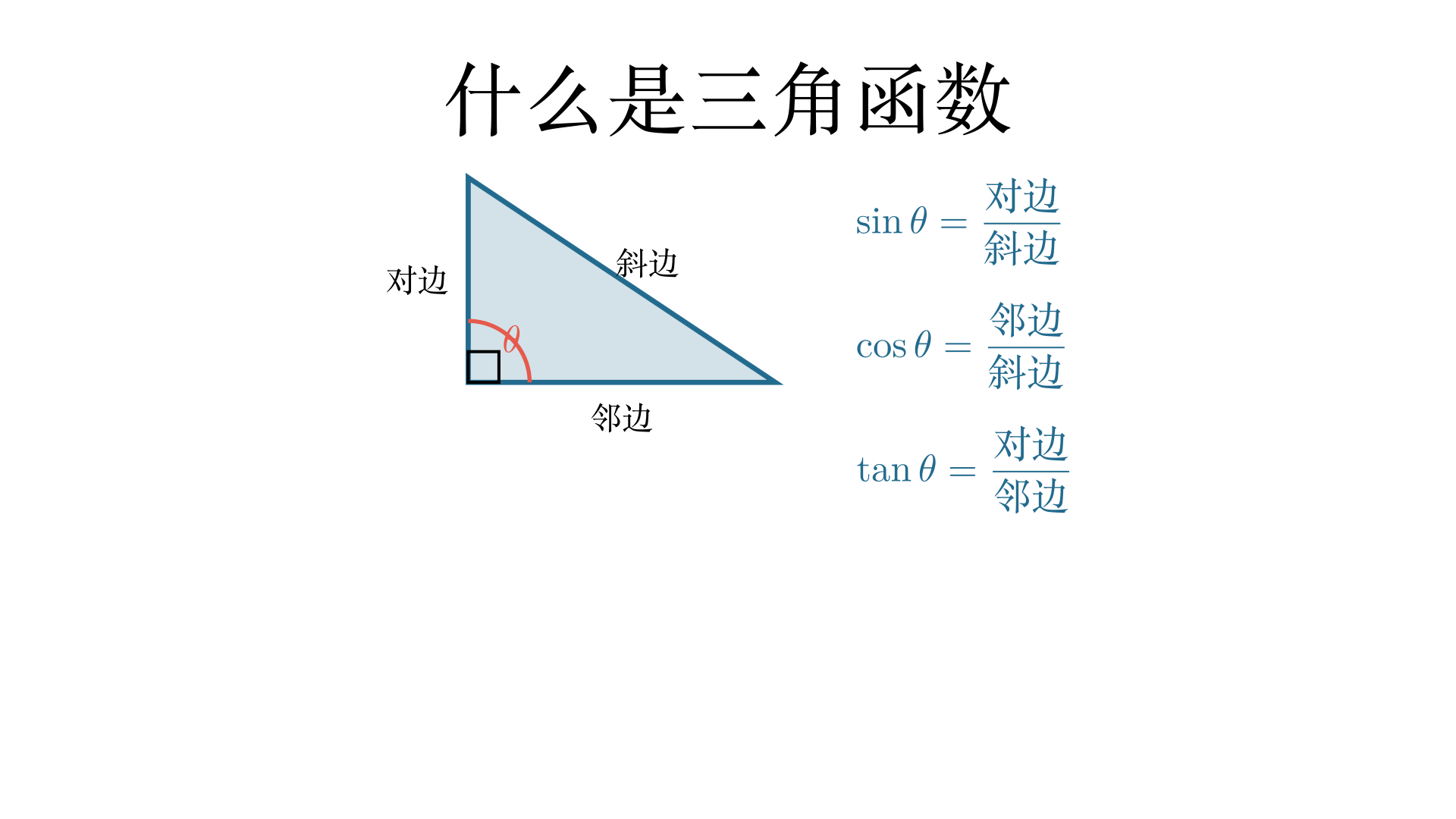
什么是三角函数
▶
4. (18 pts) A 1.0 kg particle is released from rest at the origin \(\vec{\mathbf{r}}_{0} = (0 \hat{\mathbf{i}} + 0 \hat{\mathbf{j}}) \mathrm{m}\) , and is then subject to a position-dependent force given in Newtons by \[\vec{\mathbf{F}} (x,y) = (y \hat{\mathbf{i}} -x \hat{\mathbf{j}}).\] Furthermore, the particle is constrained to a parabolic curve so that it only moves along the path \[y = 10x - x^{2}\] where both \(x\) and \(y\) are measured in meters. (a) Is this force conservative? How can you tell? (b) Calculate the work done by the force on the particle as it moves along the parabolic path to a final position \(\vec{\mathbf{r}}_{f} = (10 \hat{\mathbf{i}} + 0 \hat{\mathbf{j}}) \mathrm{m}\) . (c) What is the speed of the particle after this displacement? 解题 讲题
▶
A \(0.25 \mathrm{kg}\) block is released from rest on a frictionless ramp from a height of \(1.40 \mathrm{m}\) above the ground. At the bottom of the ramp at ground level the block runs into and compresses a spring with spring constant \(k = 2.0 \mathrm{N / cm}\) . (a) How far does the spring compress upon the block's collision? (b) How far would the spring compress if instead the block were to lose \(40\%\) of its original mechanical energy due to friction with the ramp? 使用 mathtex 显示公式
▶
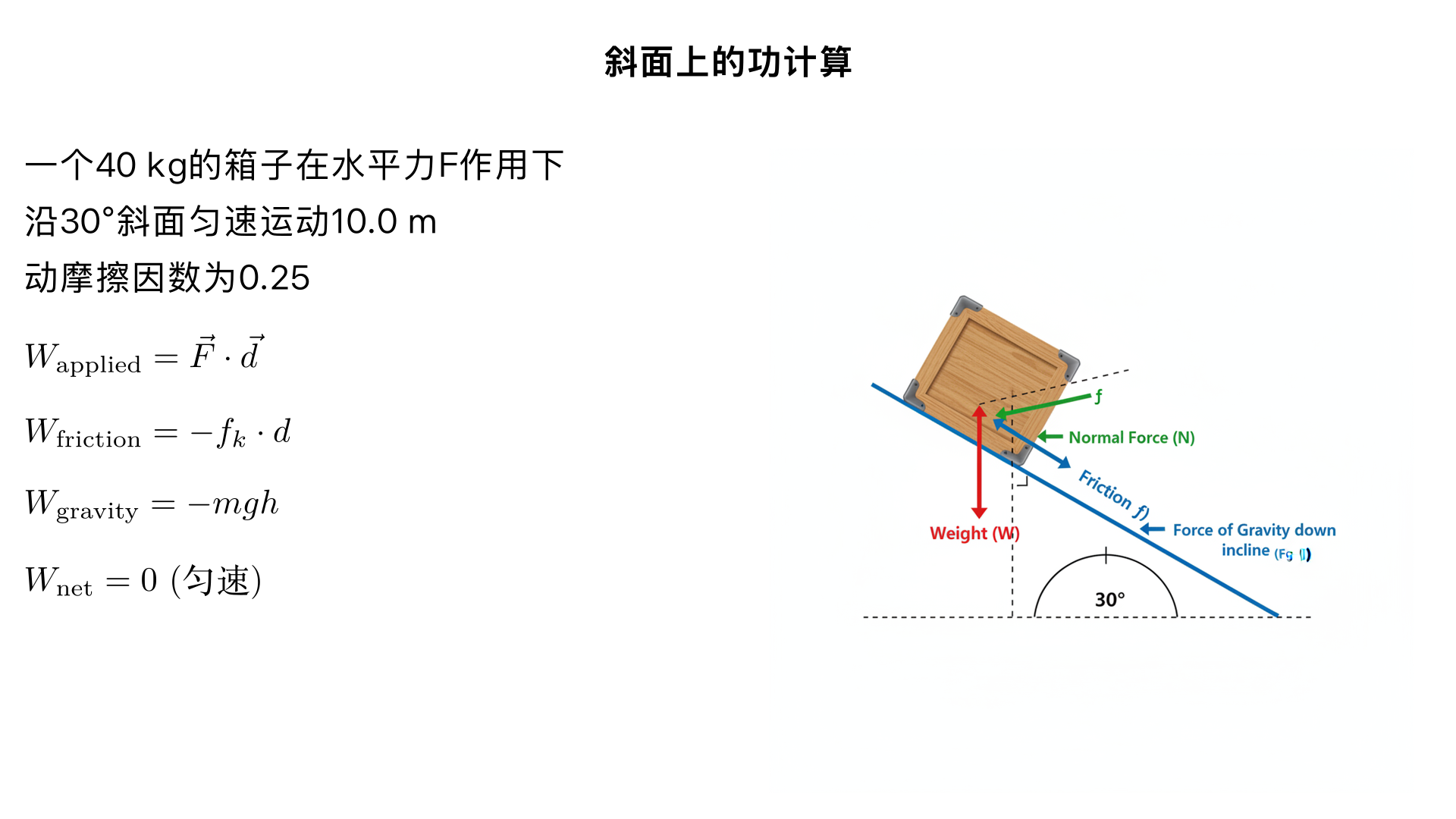
A \(40 \mathrm{kg}\) crate is pushed at constant velocity a distance \(10.0 \mathrm{m}\) along a \(30^{\circ}\) incline by the horizontal force \(\bar{\mathbf{F}}\) . The coefficient of kinetic friction between the crate and the incline is \(\mu_{k} = 0.25\) . Calculate the work done by (a) the applied force, (b) the frictional force, (c) the gravitational force, and (d) the net force.
▶