T
Teach Me AnythingTMA
Video History
Page 1 / 47
▶
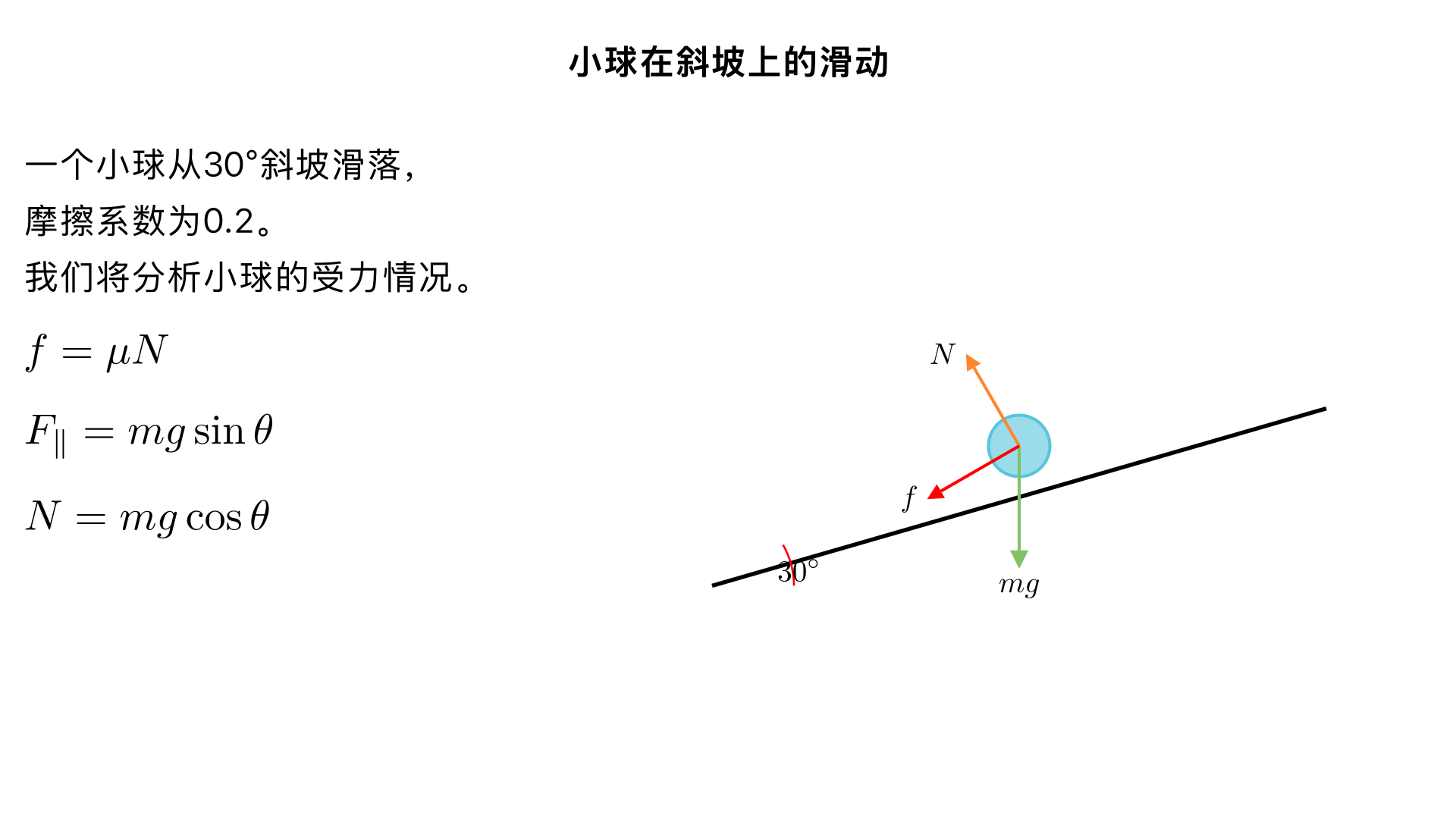
圆锥展开
▶
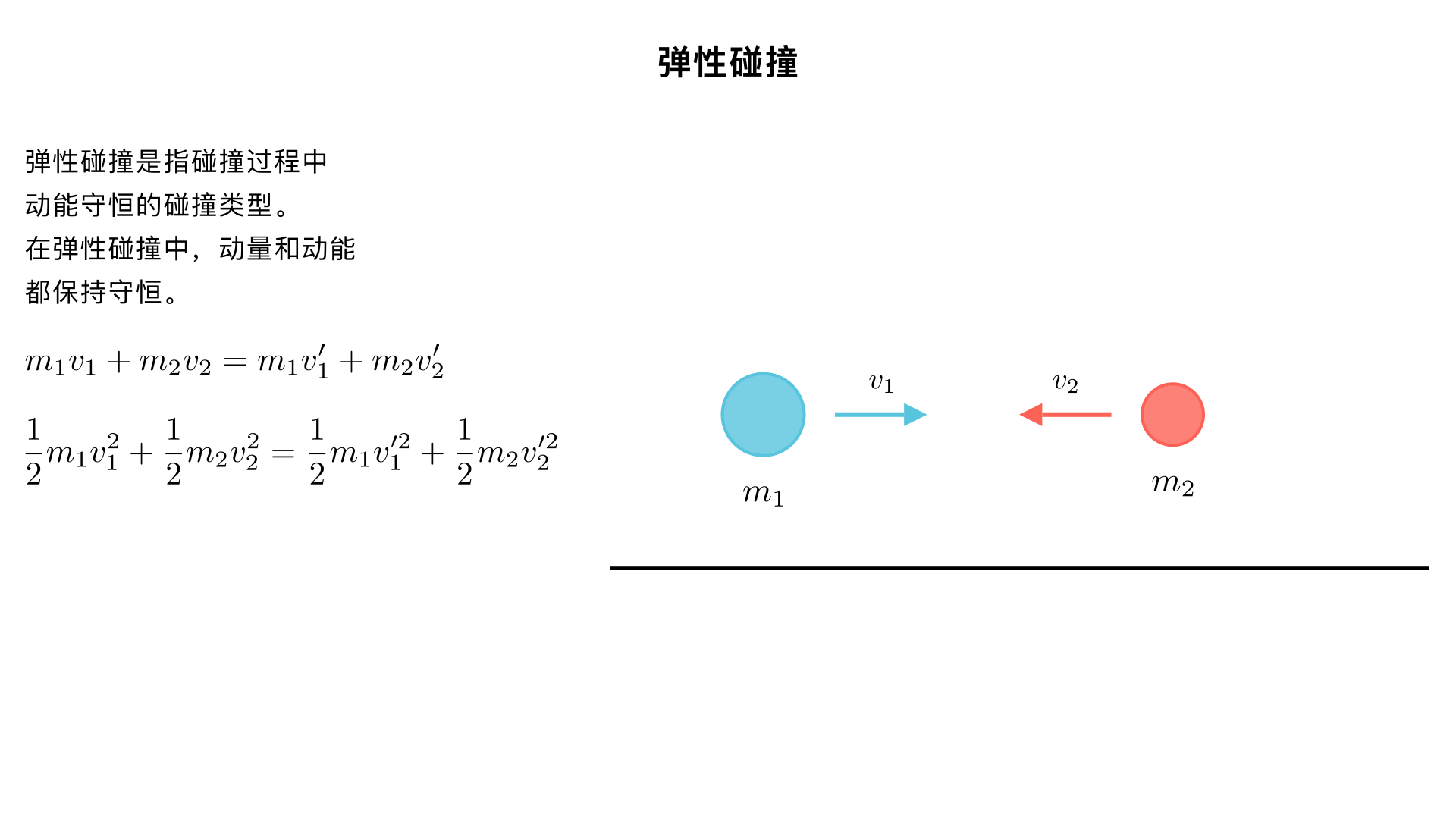
一个小球从30°斜坡滑落,摩擦系数0.2
▶
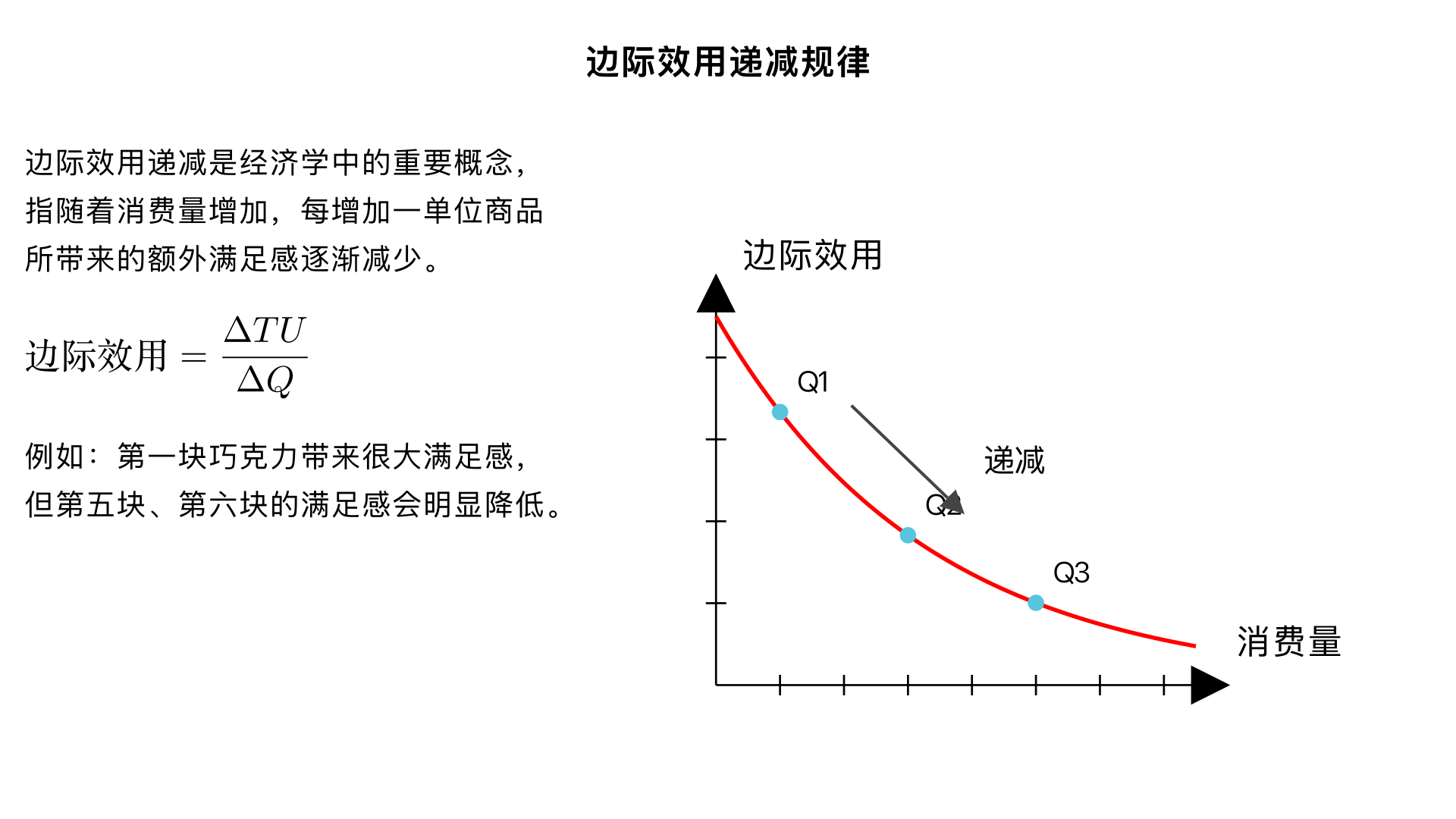
弹性碰撞
▶
解释一下 爱德思经济中的的边际效用递减
▶
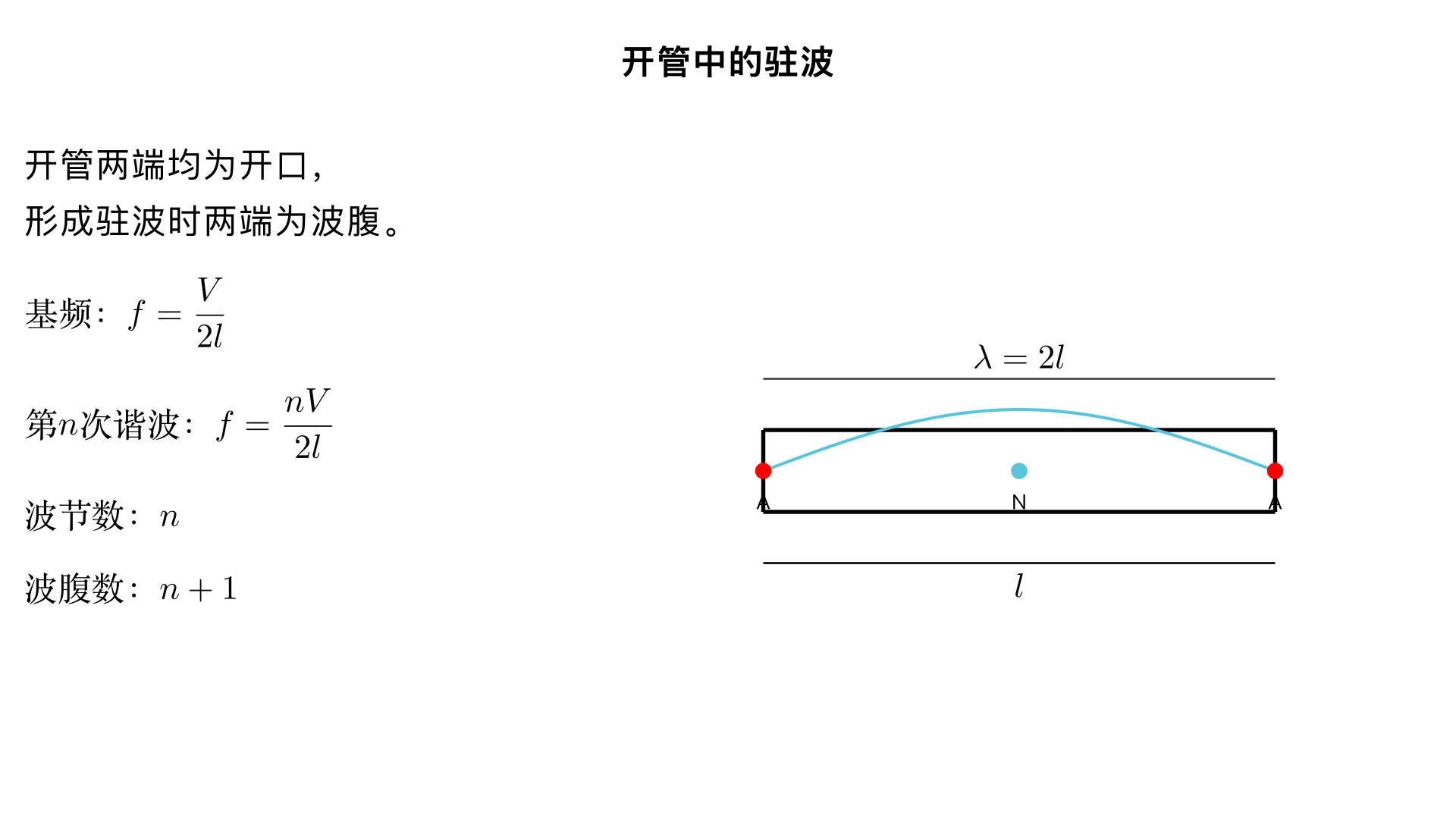
EXTRACTED_TEXT: open Organ Pipe : Standing wave form in sound A N A l = λ/2 λ = 2l f = V/λ = V/2l fundamental or wire at fixed end A N A N A λ' = l f' = V/l nᵗʰ harmonic f = nV / 2l No of Node = n No of Antinode = n+1 n = 1, 2, 3, 4, ... ... first harmonic 3rd harmonic second harmonic or first overtone MAIN_QUESTION: There is no explicit question being asked. The image serves as an explanatory slide detailing concepts related to standing waves in an open organ pipe, including definitions, formulas for frequency and harmonics, and node/antinode counts. KEY_INFORMATION: * **Topic:** Open Organ Pipe and Standing Waves. * **Fundamental mode in open organ pipe:** length l = λ/2, wavelength λ = 2l, fundamental frequency f = V/λ = V/2l. * **General formula for nᵗʰ harmonic (open organ pipe):** f = nV / 2l * **Number of Nodes for nᵗʰ harmonic:** No of Node = n * **Number of Antinodes for nᵗʰ harmonic:** No of Antinode = n+1 * **Harmonic series:** * n = 1: first harmonic * n = 2: second harmonic or first overtone * n = 3: 3rd harmonic * n = 4: ... (and so on) * **Alternative case (or wire at fixed end):** For λ' = l, frequency f' = V/l. * **Labels in diagrams:** A (Antinode), N (Node). * **Symbols:** f (frequency), V (wave speed), λ (wavelength), l (length), n (harmonic number).
▶
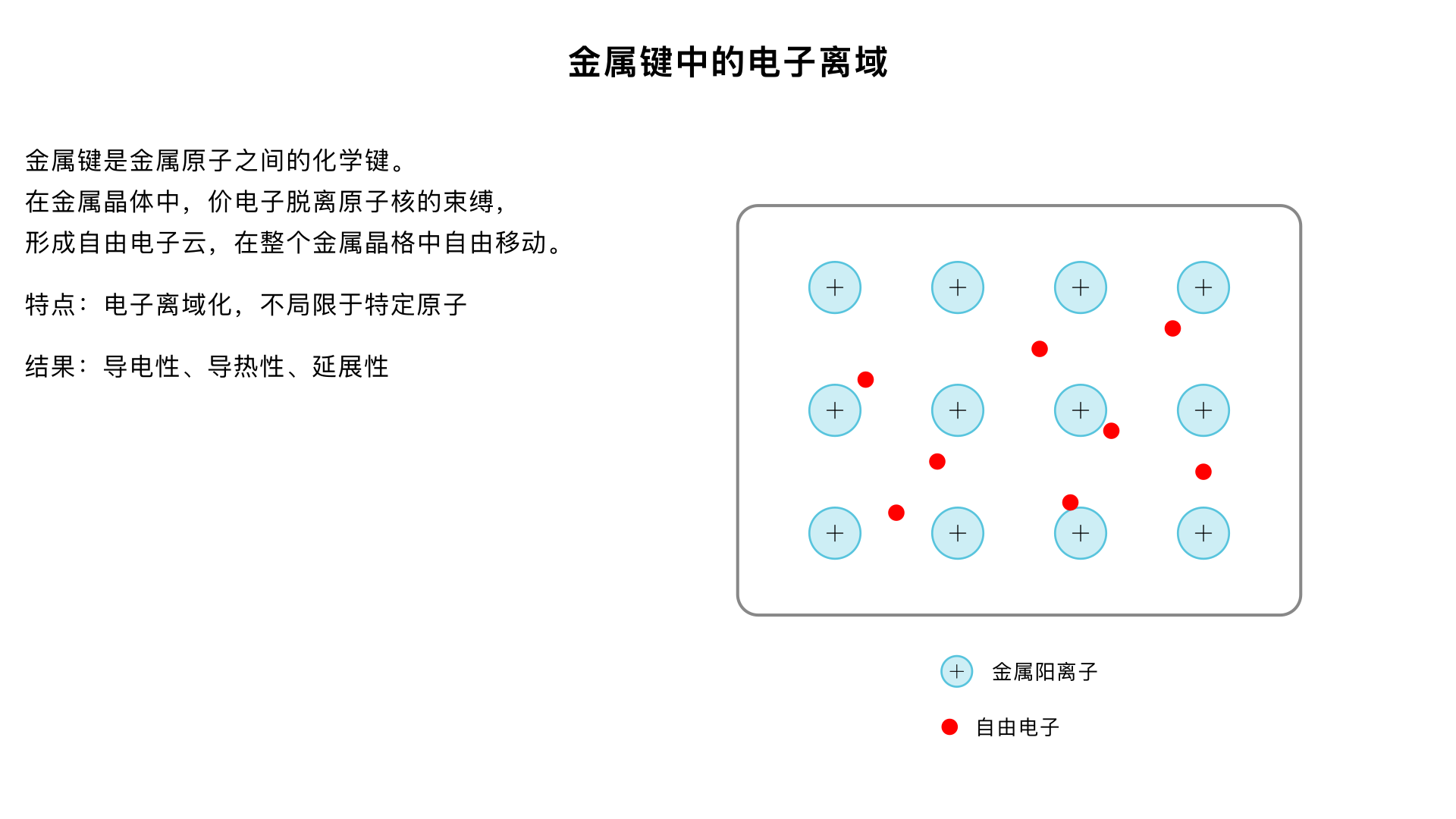
animation of delocalisation of electrons in metallic bonding
▶
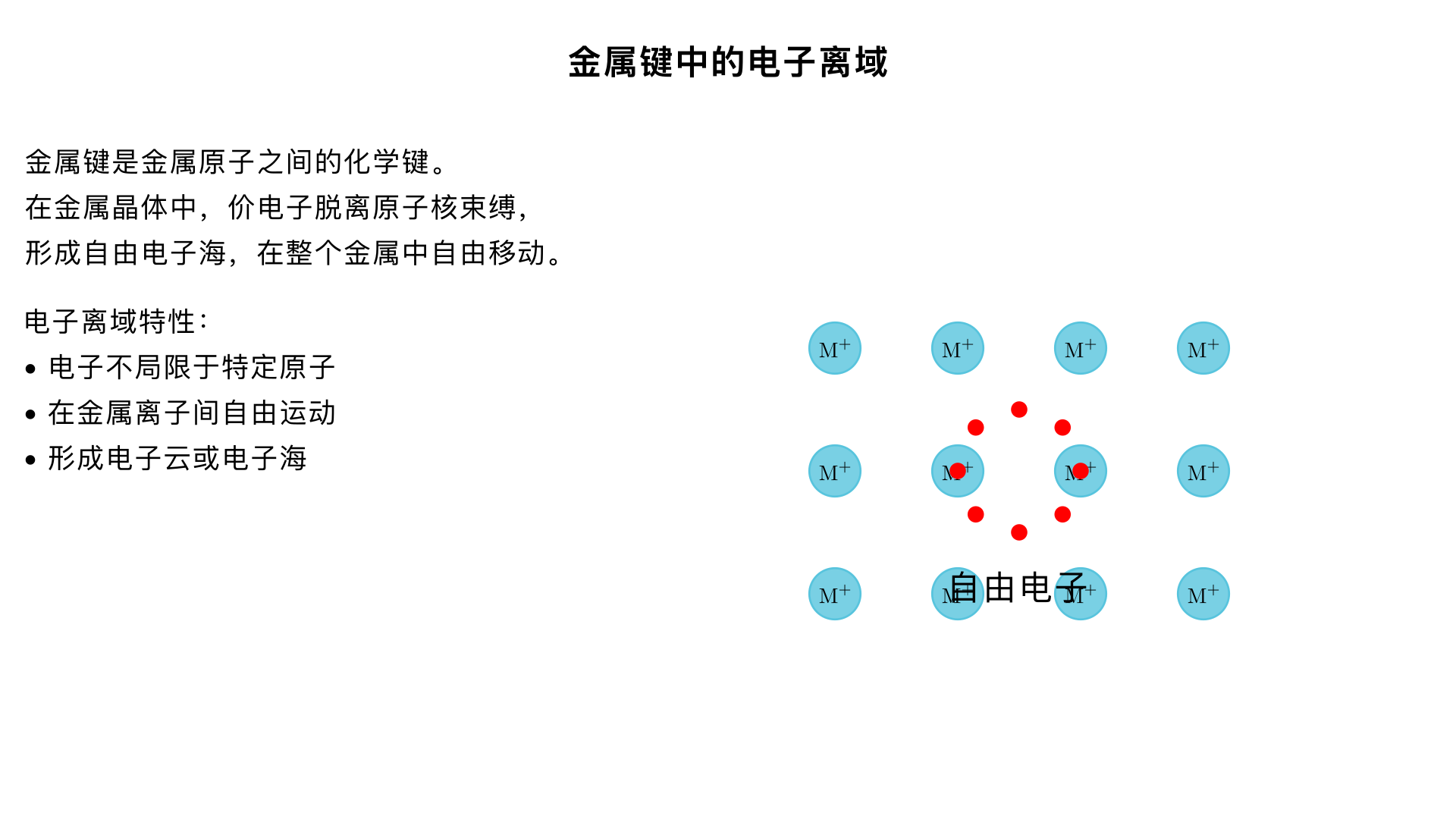
animation of delocalisation of electrons in metallic bonding
▶
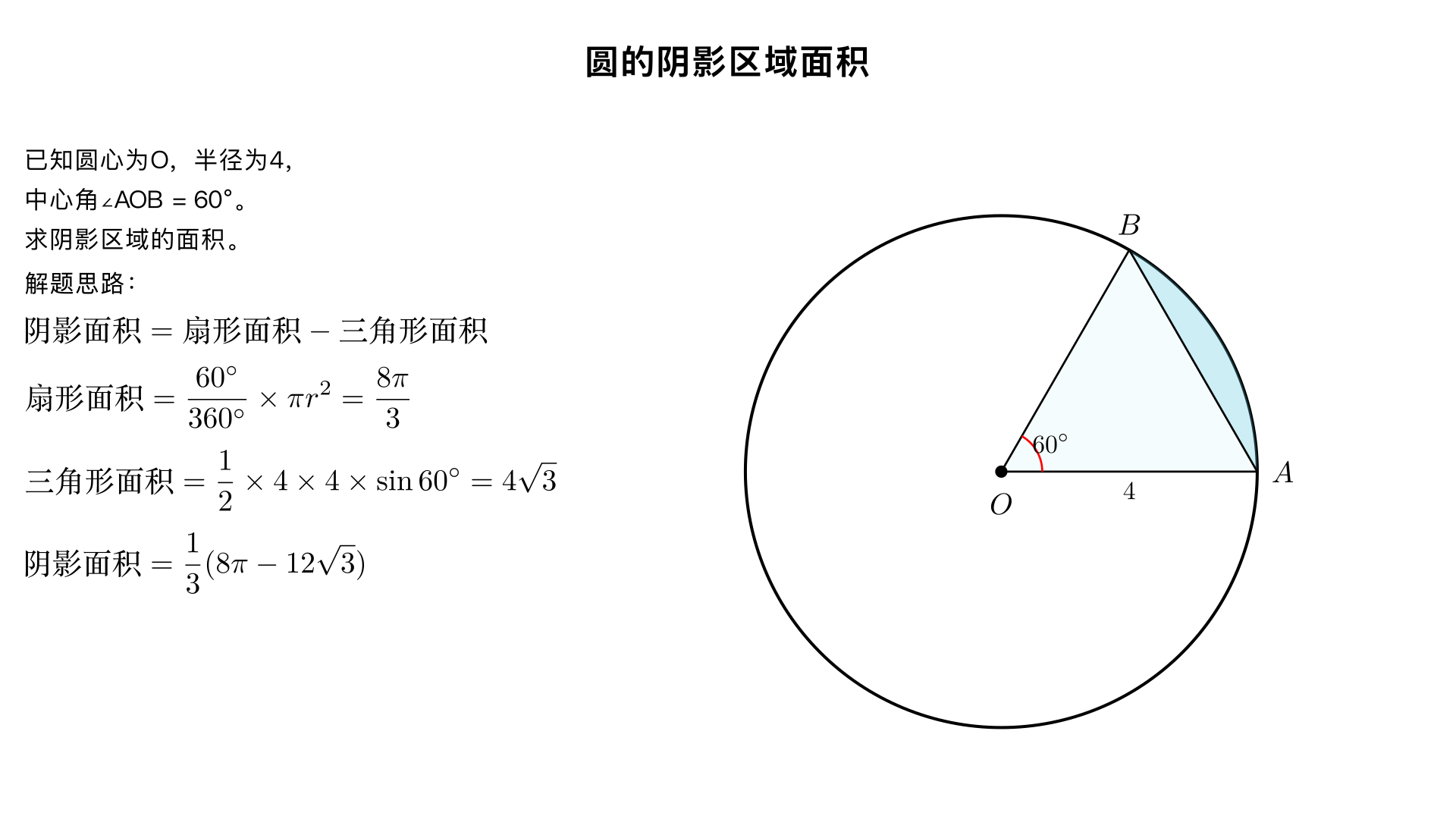
EXTRACTED_TEXT: A B 60° 4 O In the figure above, the circle has center O. What is the area of the shaded region? A) 8π/3 B) 1/3 (12√3 - 4π) C) 1/3 (8π - 8√3) D) 1/3 (8π - 12√3) MAIN_QUESTION: What is the area of the shaded region? KEY_INFORMATION: The figure contains a circle with center O. An angle at the center O is given as 60°. This angle is ∠AOB. A segment from O to B (OB) has a length of 4. The shaded region is segment of the circle, bounded by arc AB and chord AB. There are four answer choices provided: A) 8π/3 B) 1/3 (12√3 - 4π) C) 1/3 (8π - 8√3) D) 1/3 (8π - 12√3)
▶
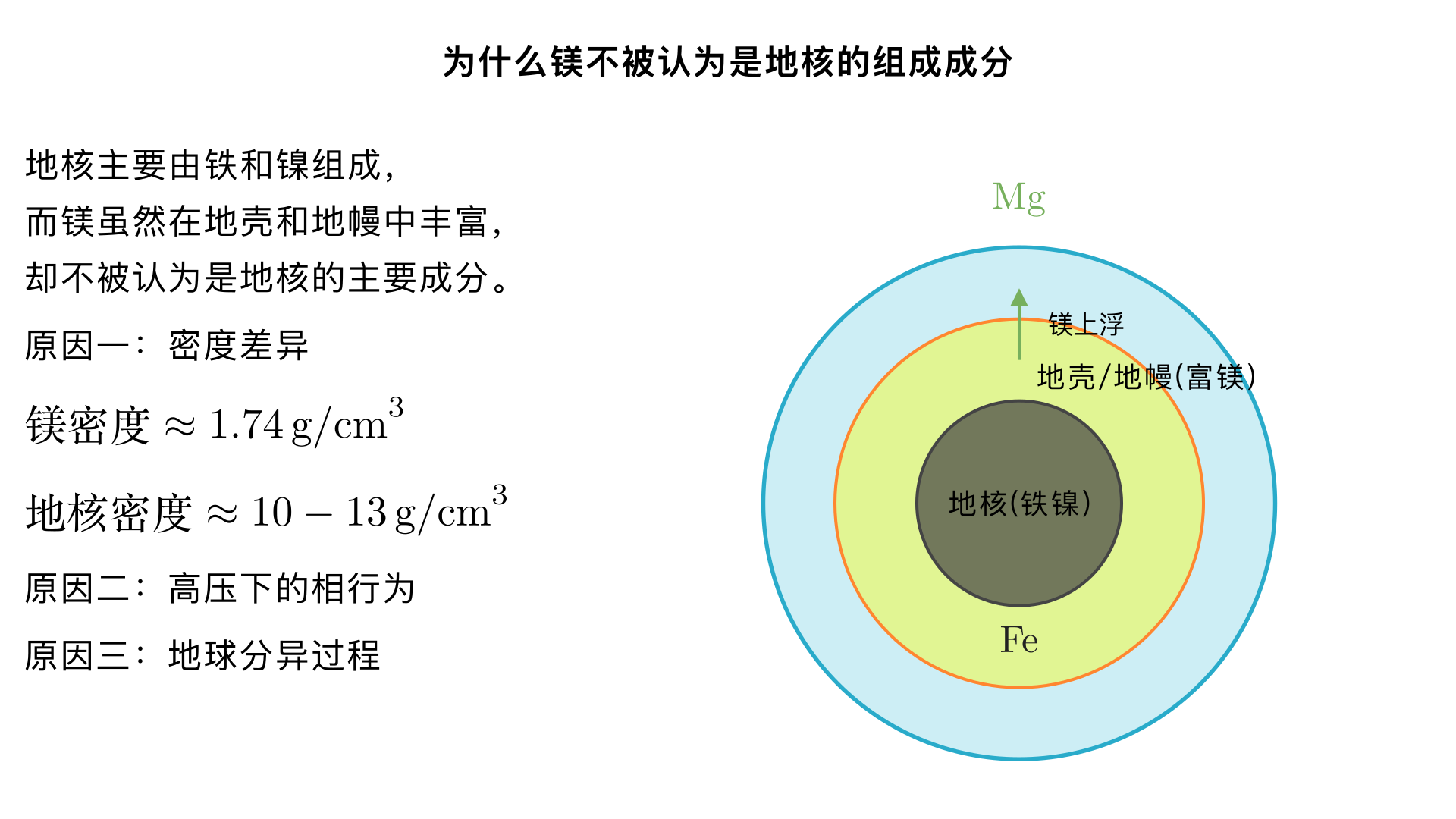
Why magnesium is not consider for earth core composition
▶
11 卦的“人际关系” II:互卦与变卦 互卦:掌握由二、三、四爻与三、四、五爻构成的新卦,洞察事物内部隐藏的动因。变卦:理解因爻动产生的卦,代表发展的最终趋势。 特色:将互卦比作“卦中卦”或“幕后故事”,将变卦视为“结果预览”。建议:以一个卦例(如“水火既济”)综合演示如何找出其互卦。
▶
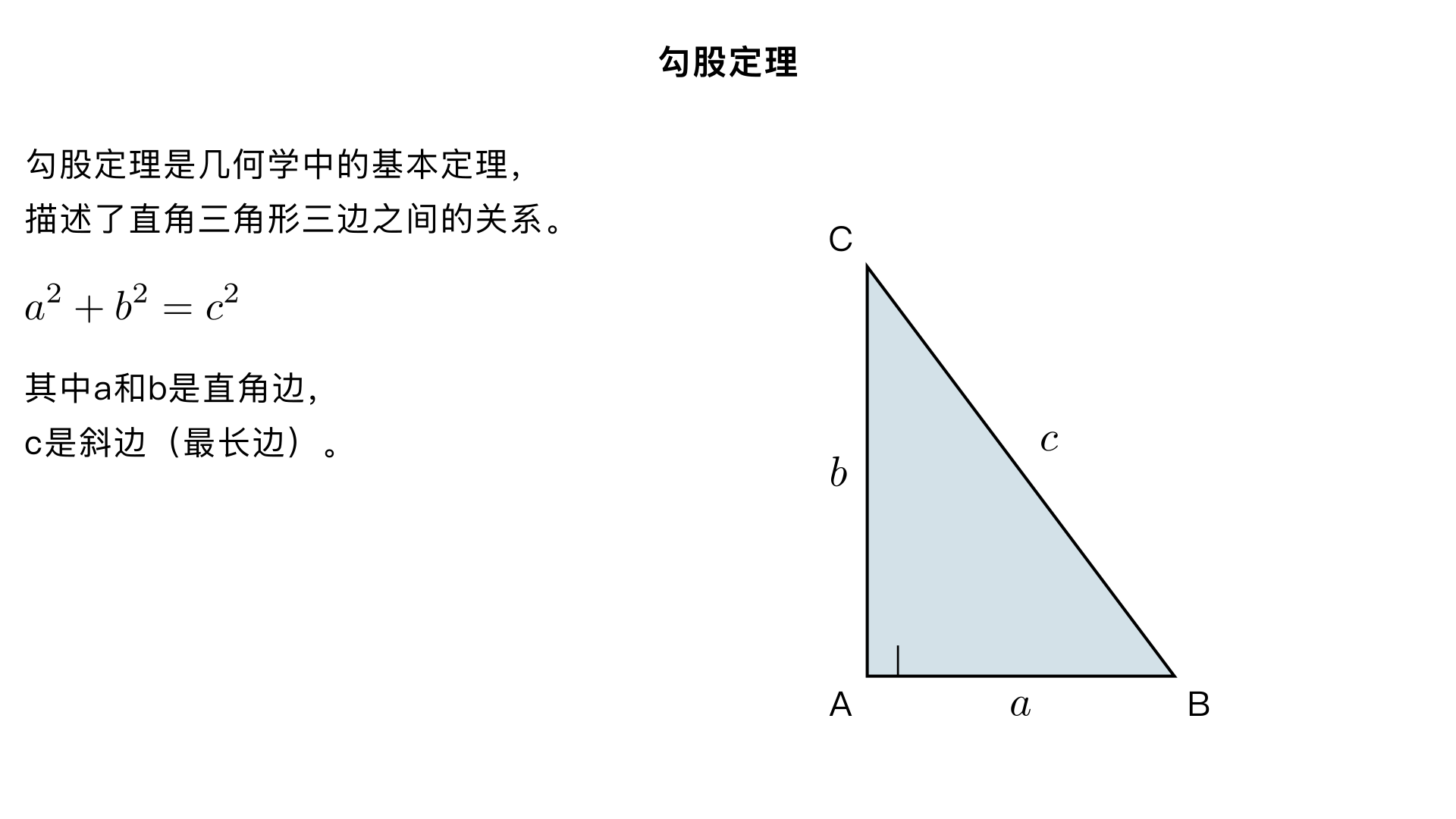
Explain pythagorean theorm
▶