T
Teach Me AnythingTMA
Video History
Page 39 / 43
▶
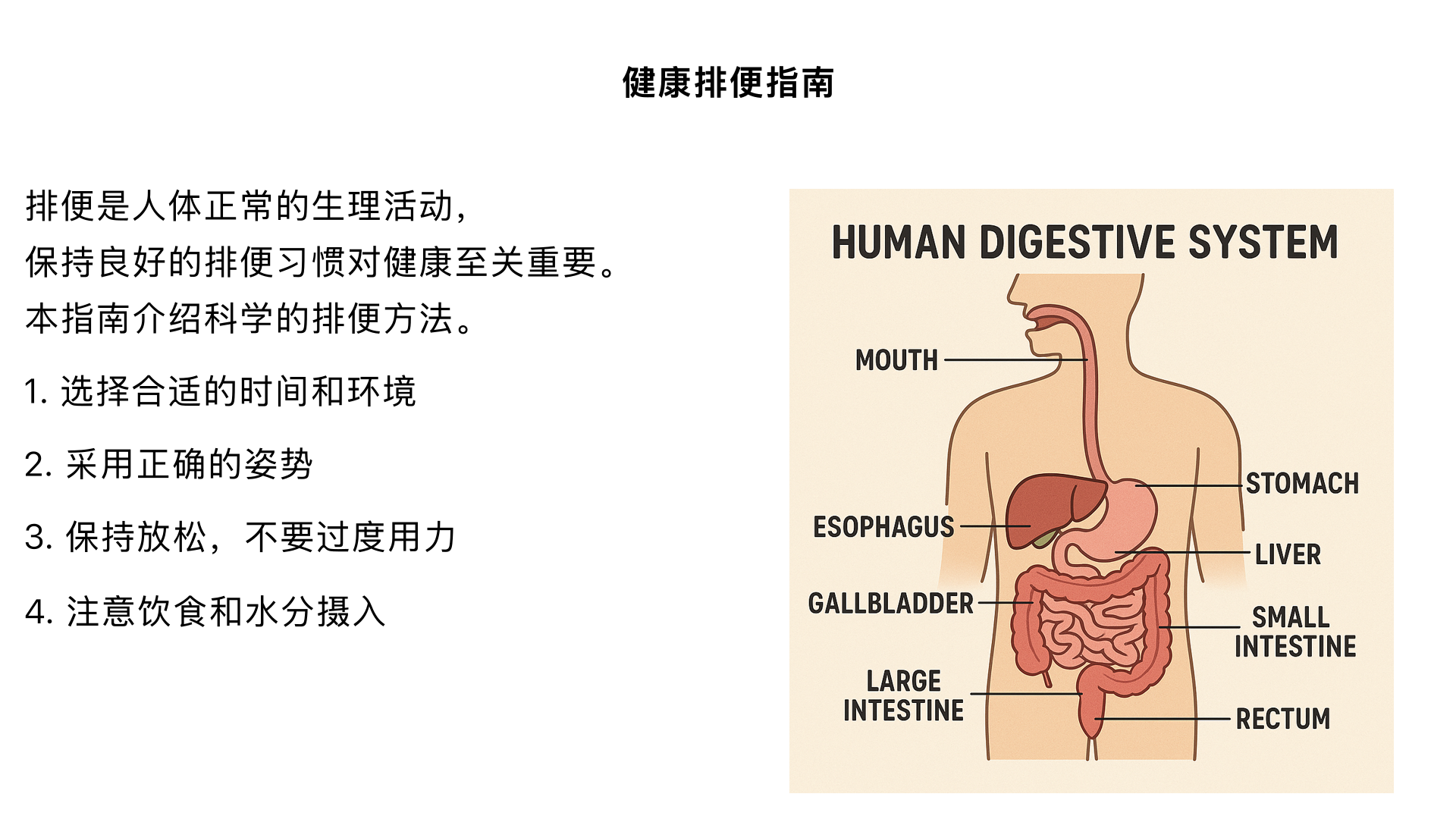
什么是RNA

▶
牛顿的知识体系有那些
▶
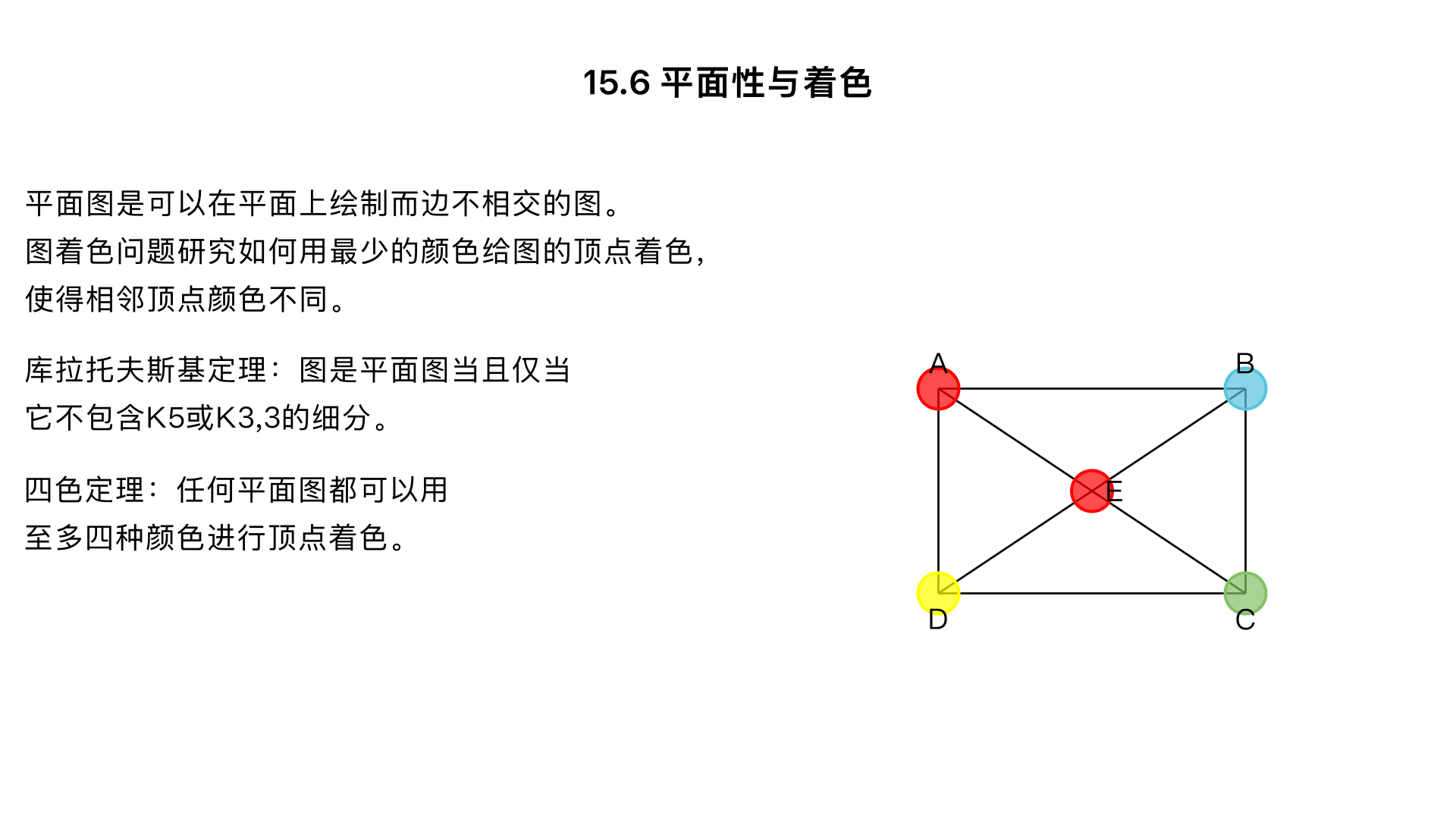
怎样拉屎

▶
怎样拉屎
▶
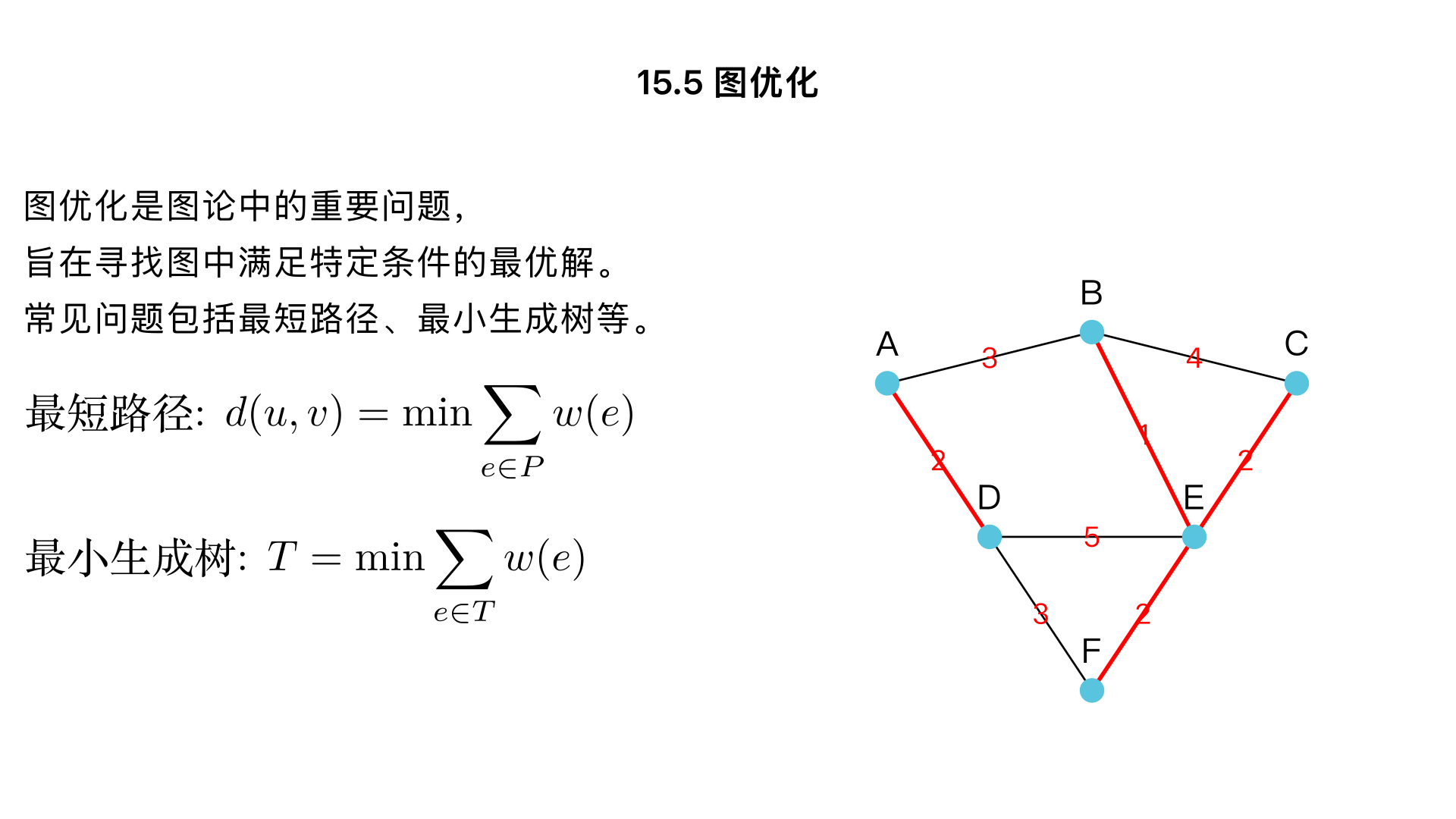
15.6 Planarity and Colorings
▶
15.5 Graph Optimization
▶
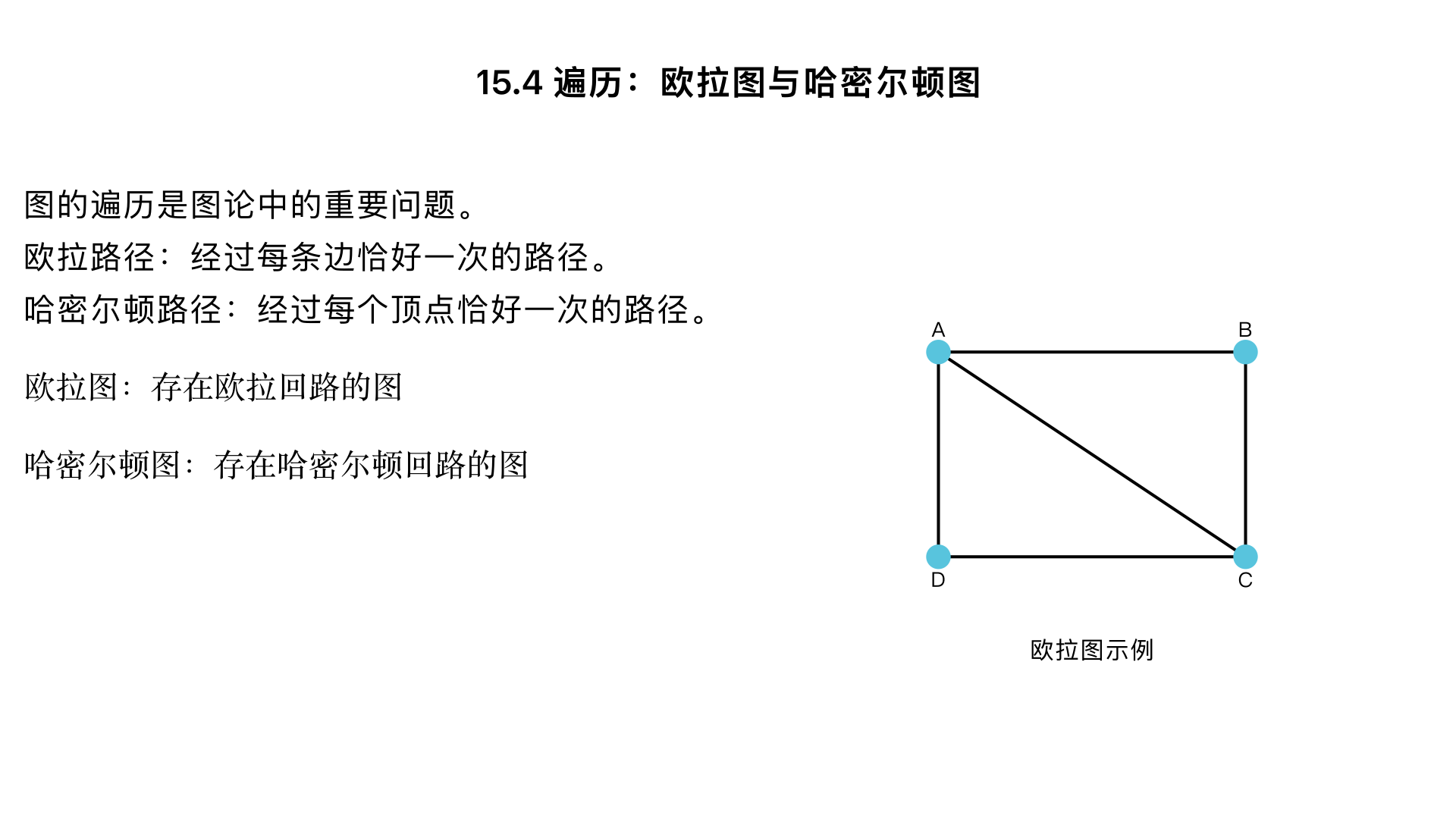
15.4 Traversals: Eulerian and Hamiltonian Graphs
▶
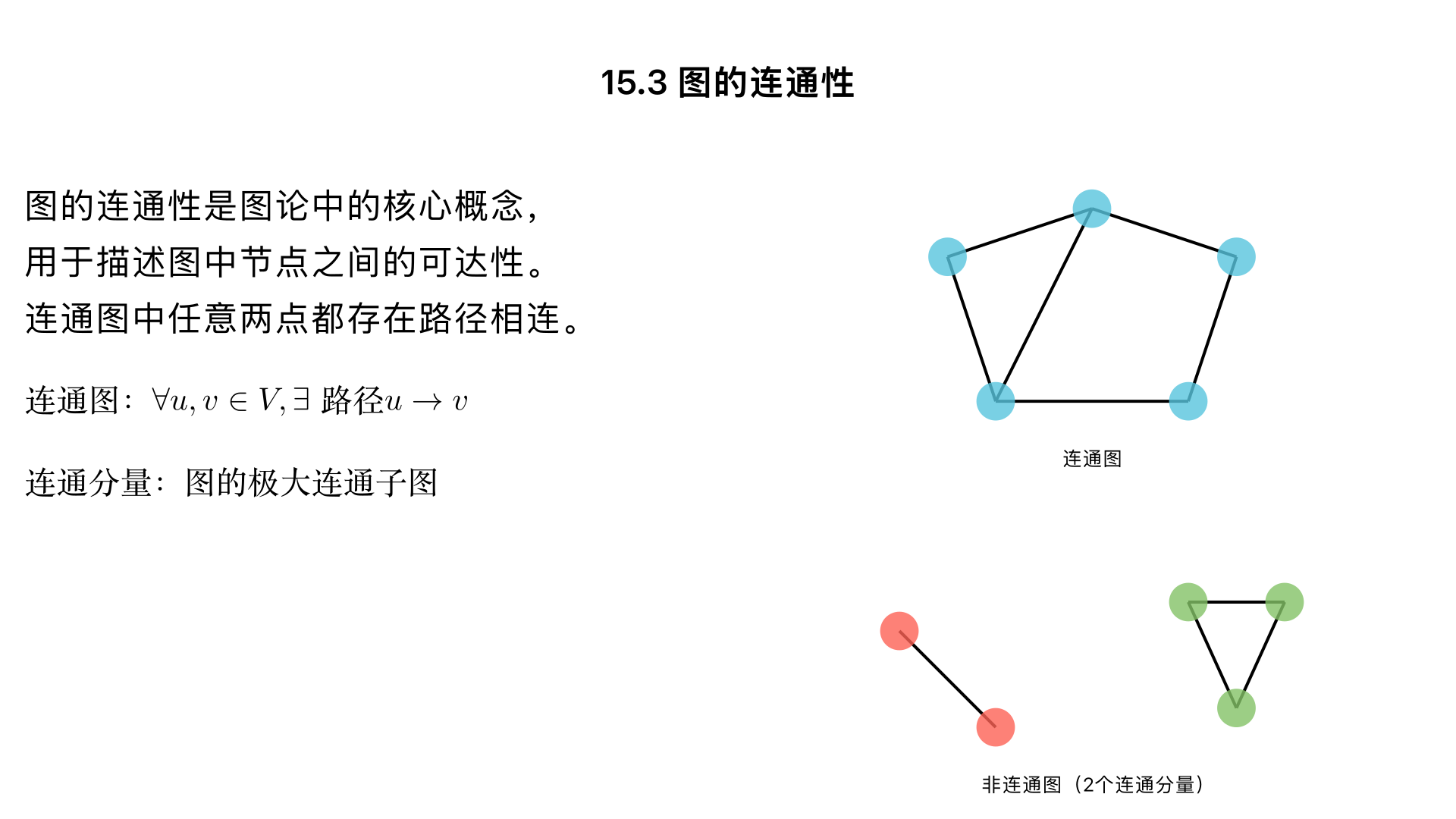
15.3 Graph Connectivity

▶
15.2 Data Structures for Graphs
▶
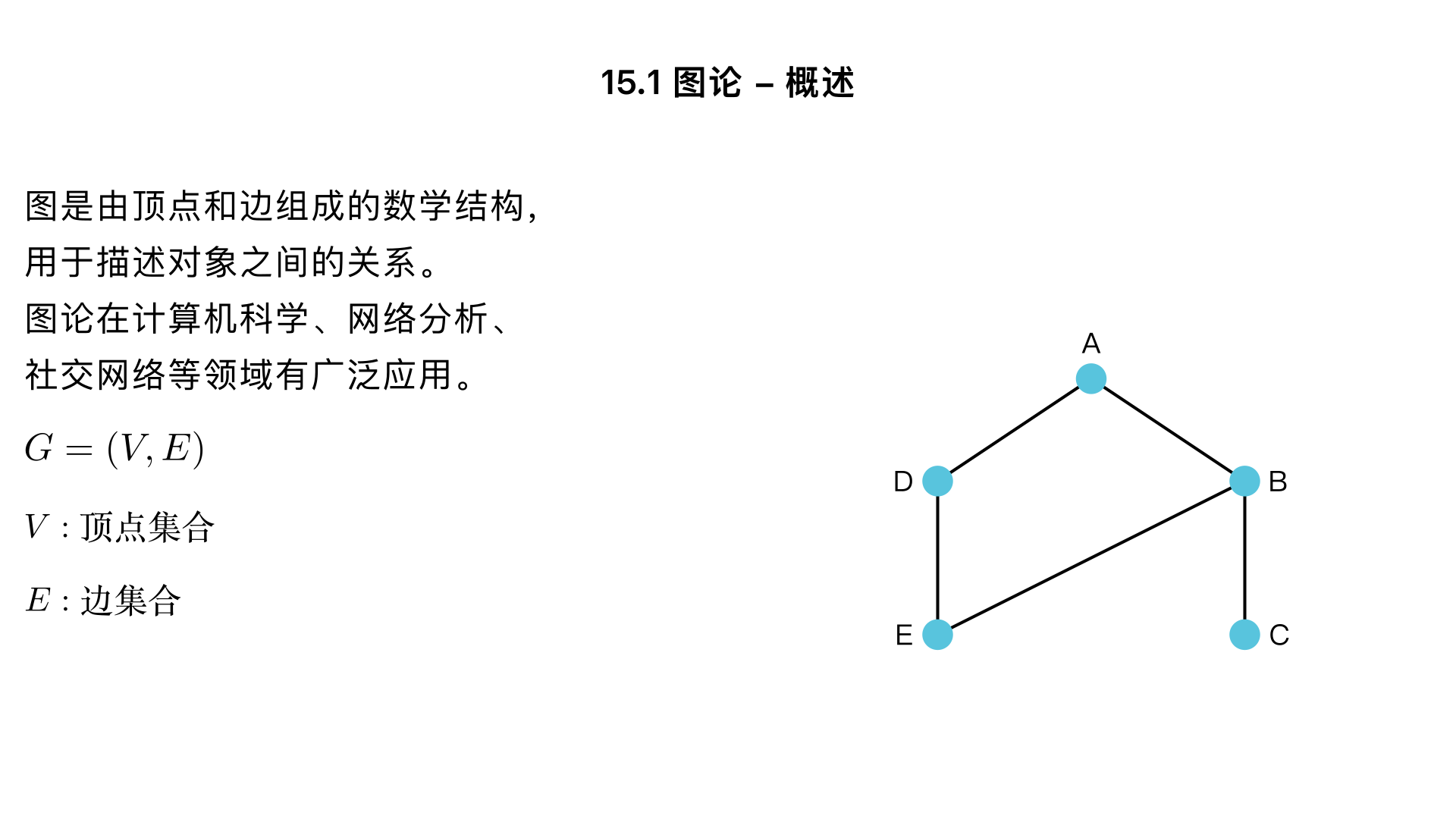
15.1 Graphs - General Introduction

▶
name:第七部分:综合实例:验证乘法程序 scene1 title:一个更复杂的例子:乘法程序 scene1 content:现在,我们将运用之前学到的所有知识,来验证一个计算两个整数乘积的程序。这个程序包含了条件判断和循环,是一个很好的综合练习。 scene2 title:验证策略:分段与组合 scene2 content:我们的策略是将整个程序分解为四个逻辑片段S1, S2, S3, S4。然后,我们逐一证明每个片段的正确性,最后使用组合规则将它们串联起来,证明整个程序的正确性。 scene3 title:验证S1:处理负数 scene3 content:第一段S1是一个if-else语句,它计算n的绝对值并存入变量a。我们可以证明,在S1执行后,断言 q: 'a = |n|' 成立。这与我们之前验证if-then-else的例子类似。 scene4 title:验证S2:初始化 scene4 content:第二段S2是初始化语句,k:=0, x:=0。在S2执行后,我们可以得到新的断言 r: 'q ∧ (k=0) ∧ (x=0)' 成立。 scene5 title:验证S3:核心循环 scene5 content:第三段S3是while循环。我们需要找到它的循环不变量。这里的循环不变量是 v: 'x = m*k ∧ k ≤ a'。我们需要证明v确实是不变量,并且循环会终止。 scene6 title:证明S3的循环不变量和终止性 scene6 content:首先,在循环开始前,k=0, x=0,满足x=m*k。其次,在循环体内,x增加m,k增加1,不变量关系'x=m*k'得以维持。最后,因为k从0开始每次加1,它最终会等于a,导致循环终止。 scene7 title:S3循环结束后的状态 scene7 content:根据迭代规则,当循环结束时,循环条件k<a为假,且不变量v为真。这意味着 k=a 且 x=m*k,所以我们得到 x = m*a。结合之前的a=|n|,我们得到 x = m*|n|。 scene8 title:验证S4:最终结果调整 scene8 content:第四段S4根据n的符号来确定最终结果。如果n<0,product=-x;否则product=x。我们可以证明,无论哪种情况,最终的product都等于m*n。 scene9 title:最终结论:组合所有证明 scene9 content:我们已经证明了从p{S1}q, q{S2}r, r{S3}s, 到s{S4}t的每一步都是正确的。根据组合规则,我们可以得出最终结论 p{S}t,即整个程序对于任意整数输入m和n,都能正确计算出它们的乘积m*n。课程到此结束,谢谢大家!

▶