T
Teach Me AnythingTMA
Video History
Page 20 / 43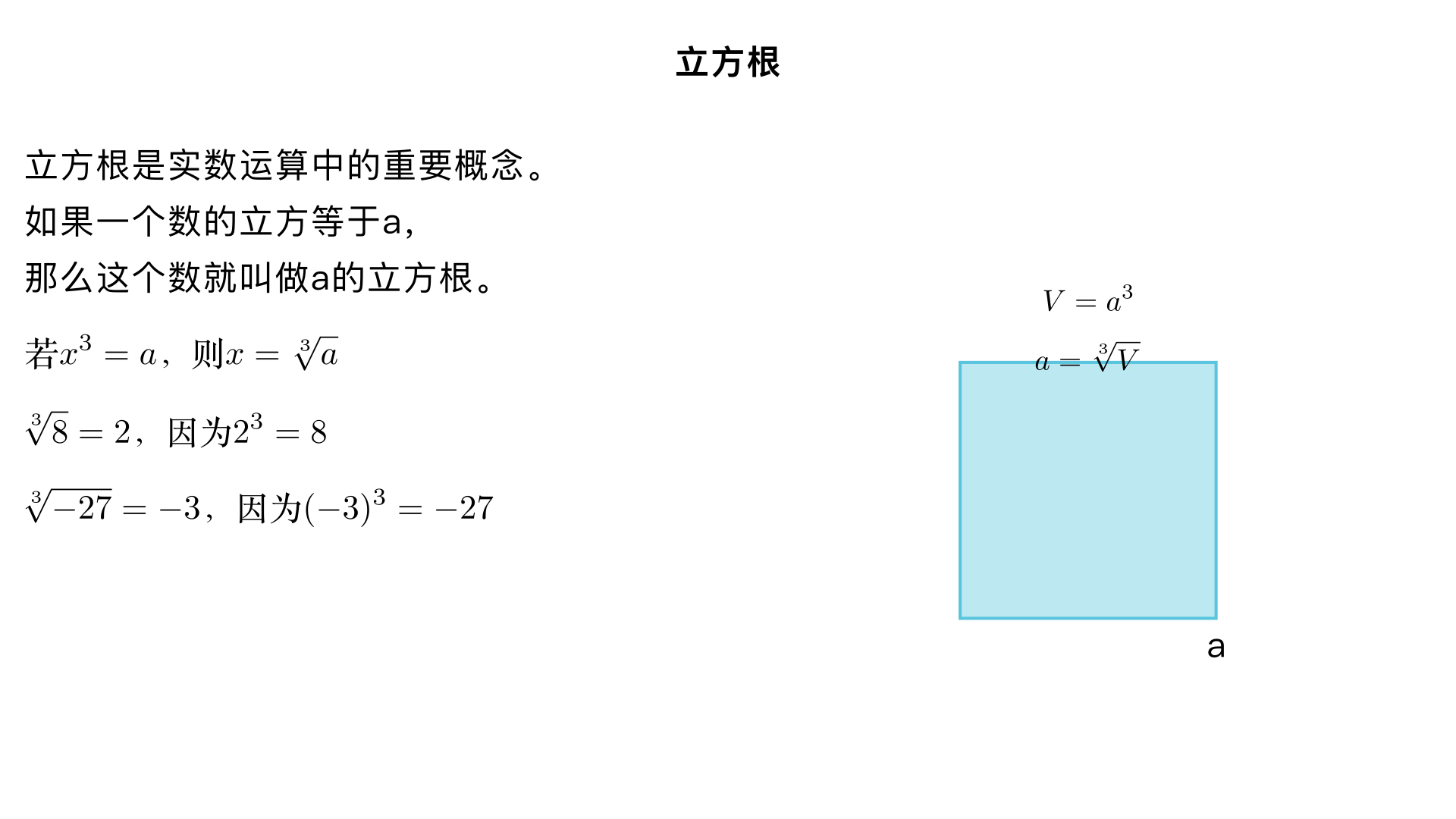
▶
七年级数学 / 实数 / 立方根 一、立方根的基本定义 如果一个数的立方等于 a ,那么这个数就叫做 a 的立方根,也叫做 a 的三次方根。 数学表达式:若 x 3 =a ,则 x 叫做 a 的立方根,记作 x= 3 a ,其中符号 “ 3 ” 称为三次根号, a 是被开方数,根指数 3 不能省略(平方根的根指数 2 可省略)。 示例:因为 2 3 =8 ,所以 8 的立方根是 2 ,即 3 8 =2 ;因为 (−2) 3 =−8 ,所以 −8 的立方根是 −2 ,即 3 −8 =−2 。 二、立方根的核心性质 唯一性:任何实数都有且只有一个立方根。 与平方根不同(负数没有平方根),正数、负数、 0 都能找到唯一的立方根。 符号性: 正数的立方根是正数,例如 3 27 =3 ; 负数的立方根是负数,例如 3 −64 =−4 ; 0 的立方根是 0 ,即 3 0 =0 。 特殊等式: 3 −a =− 3 a ,即负数的立方根可转化为其相反数的立方根的相反数,比如 3 −125 =− 3 125 =−5 。 三、立方根的计算方法 开立方与立方互为逆运算:求一个数的立方根,可通过找哪个数的立方等于被开方数来确定。 示例:求 3 64 ,因为 4 3 =64 ,所以 3 64 =4 ;求 3 − 8 1 ,因为 (− 2 1 ) 3 =− 8 1 ,所以 3 − 8 1 =− 2 1 。 常见立方根数值(需熟记): 被开方数 a 3 a 被开方数 a 3 a 0 0 −1 −1 1 1 −8 −2 8 2 −27 −3 27 3 −64 −4 64 4 −125 −5 四、立方根与平方根的区别 对比维度 平方根 立方根 存在范围 非负数才有平方根 全体实数都有立方根 个数 正数有两个互为相反数的平方根, 0 的平方根是 0 任何实数都只有一个立方根 符号 正数的平方根一正一负 正数立方根为正,负数立方根为负 根指数 根指数 2 可省略 根指数 3 不可省略 五、立方根的简单应用 利用立方根可解决与体积相关的实际问题,比如求正方体的棱长。 示例:一个正方体的体积为 216 立方厘米,求其棱长。设棱长为 x 厘米,则 x 3 =216 ,解得 x= 3 216 =6 ,即棱长为 6 厘米。
▶
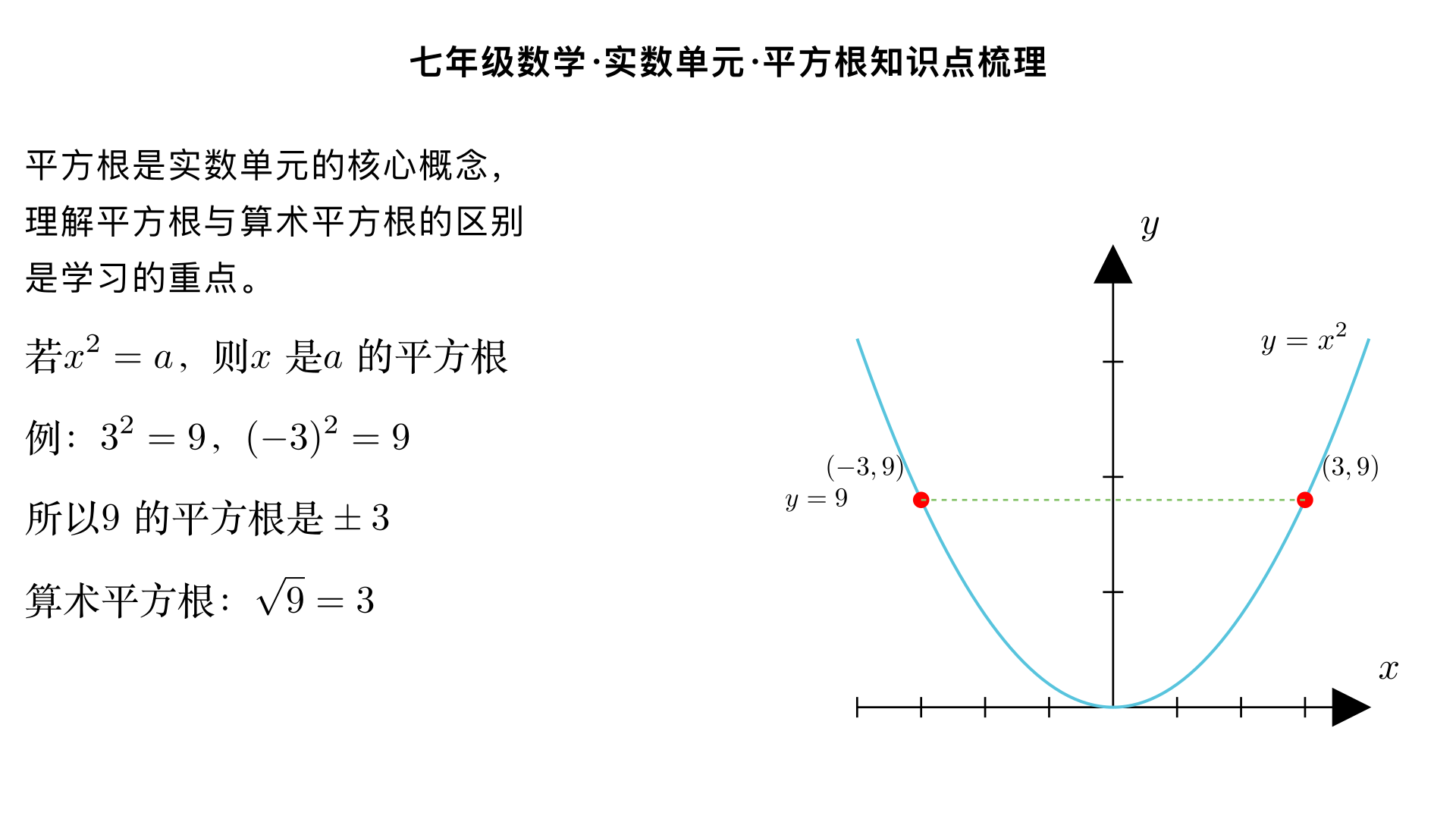
七年级数学・实数单元・平方根知识点梳理 一、平方根的基础定义 如果一个数 x 的平方等于 a (即 x 2 =a ),那么这个数 x 就叫做 a 的平方根,也叫做二次方根。 示例:因为 3 2 =9 , (−3) 2 =9 ,所以 9 的平方根是 3 和 −3 ,记作 ± 9 =±3 。 符号说明: 称为根号, a 称为被开方数,且被开方数 a 必须满足 a≥0 (因为任何实数的平方都非负,负数没有平方根)。 二、算术平方根 1. 定义 正数 a 的正的平方根叫做 a 的算术平方根,记作 a ;特别地, 0 的平方根和算术平方根都是 0 (即 0 =0 )。 示例: 9 的算术平方根是 9 =3 ,而 −3 是 9 的平方根但不是算术平方根。 2. 算术平方根的非负性 算术平方根 a 具有双重非负性: 被开方数非负: a≥0 ; 算术平方根本身非负: a ≥0 。 常见题型:若 x−2 + y+3 =0 ,则 x−2=0 且 y+3=0 ,即 x=2 , y=−3 。 三、平方根的性质 正数的性质:一个正数有两个平方根,它们互为相反数(如 16 的平方根为 ±4 )。 0 的性质: 0 的平方根只有一个,就是 0 本身。 负数的性质:负数没有平方根(因为实数范围内,任何数的平方都不可能是负数)。 四、平方根的计算方法 完全平方数的平方根:直接根据平方逆运算求解,如 25 =5 , ± 49 =±7 。 非完全平方数的平方根:结果为无理数,可保留根号形式或求近似值,如 2 ≈1.414 , 3 ≈1.732 (七年级阶段通常要求保留根号或记住常用近似值)。 五、易错点辨析 混淆平方根和算术平方根:如 16 =4 (算术平方根,只有正根),而 16 的平方根是 ±4 (两个根)。 忽略被开方数的非负性:如误认为 −4 有意义,实际负数无平方根。 错误计算带分数平方根:如 1 16 9 需先化为假分数 16 25 = 4 5 ,而非直接拆分计算。
▶
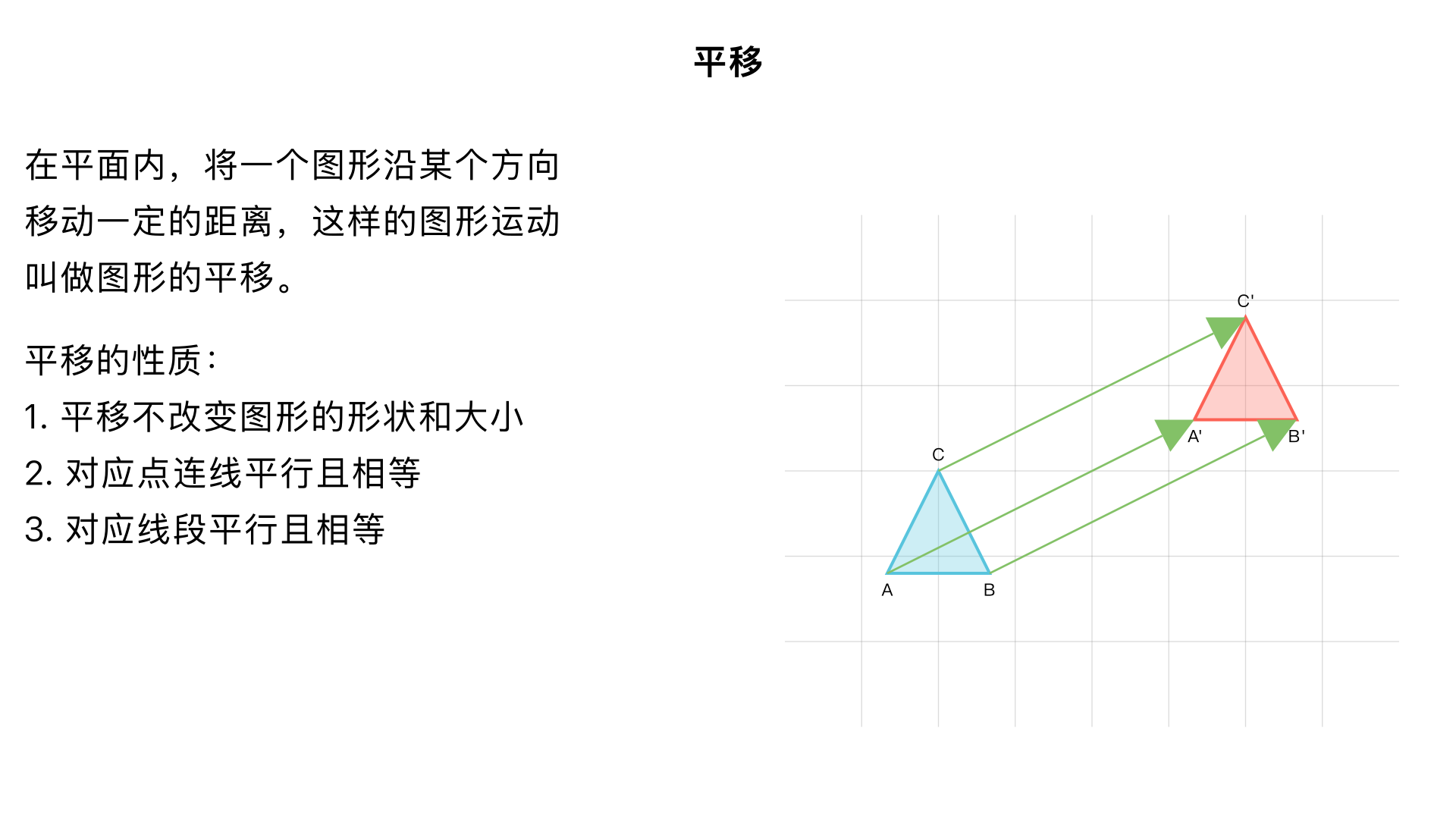
七年级数学・相交线与平行线・平移 一、平移的定义 在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动叫做图形的平移,简称平移。 需要注意的是: 平移的两大要素:平移方向(如水平向左、竖直向上、斜向右下等)和平移距离(图形上任意一点移动的路程); 平移只改变图形的位置,不改变图形的形状、大小和方向。 示例:在方格纸中把一个三角形向右移动 5 个单位长度,就是典型的平移运动。 二、平移的性质 平移前后的两个图形是全等图形,对应边相等、对应角相等; 连接各组对应点的线段平行(或在同一条直线上)且相等; 对应线段平行(或在同一条直线上)且相等,对应角相等。 示例:将线段 AB 平移得到线段 A'B',则 AB∥A'B'(或共线)且 AB=A'B',连接 AA' 和 BB',有 AA'∥BB'(或共线)且 AA'=BB'。 三、平移的作图步骤 以平移三角形 ABC,使点 A 移到点 A' 为例,步骤如下: 确定平移方向和距离:方向为从 A 到 A' 的方向,距离为线段 AA' 的长度; 作对应点: 过点 B 作线段 BB'∥AA',且 BB'=AA',得到点 B 的对应点 B'; 过点 C 作线段 CC'∥AA',且 CC'=AA',得到点 C 的对应点 C'; 连接对应点:顺次连接 A'B'、B'C'、C'A',得到平移后的三角形 A'B'C'。 四、平移与平行线的关联 平移的本质是利用了平行线的性质,因为平移过程中对应点连线和对应线段都保持平行; 反过来,也可以借助平行线来验证图形是否为平移得到(若对应点连线都平行且相等,则是平移变换)。 五、平移的实际应用 生活中的平移现象:电梯的升降、传送带上物品的移动、窗户的推拉等; 数学解题中的应用:通过平移线段或图形,将分散的线段集中到一起,方便计算长度或角度(如求不规则图形的周长、面积)。
▶
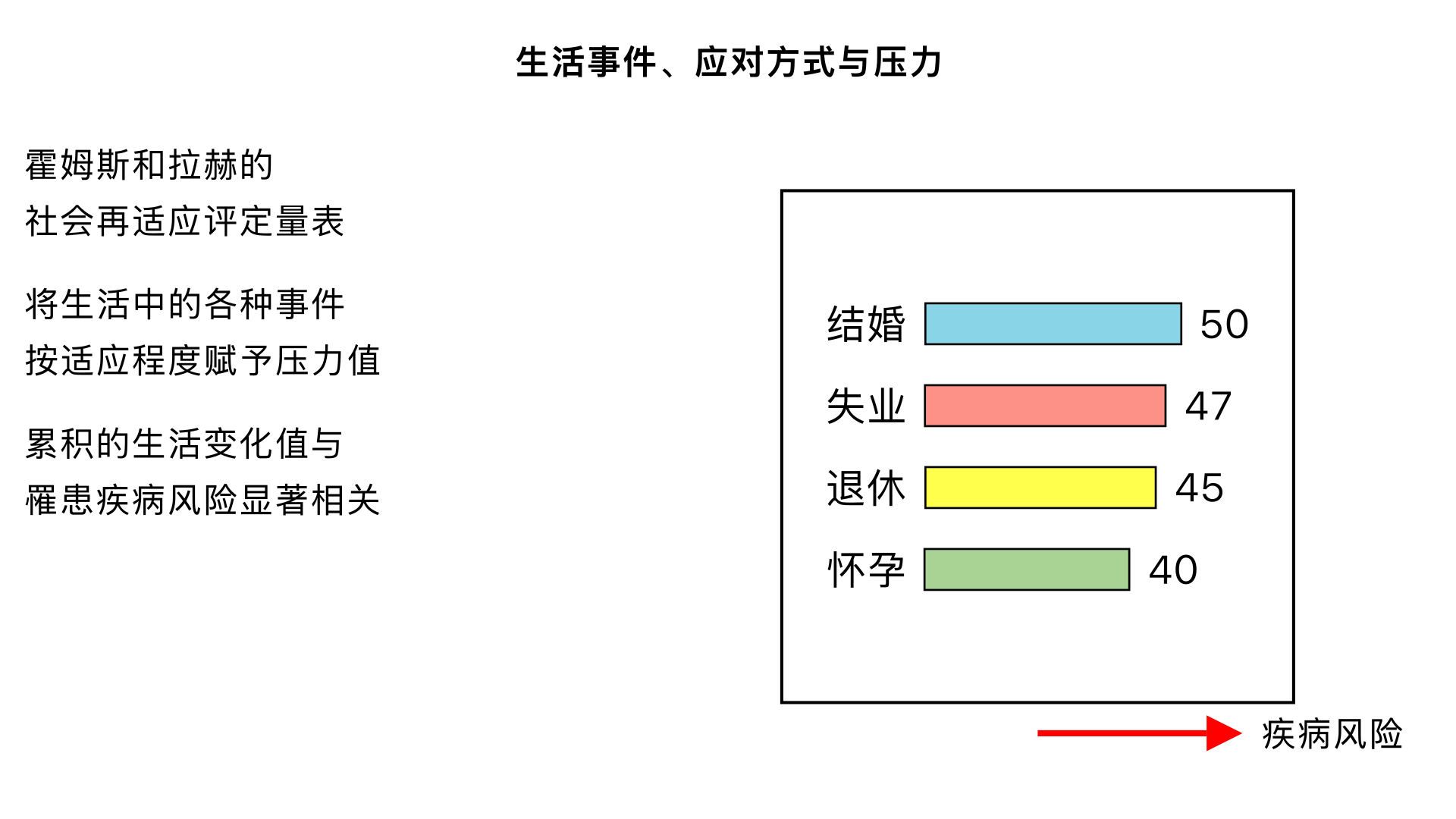
生活事件、应对方式与压力 (霍姆斯和拉赫的“社会再适应评定量表”) 主要内容:编制了一个量表,将生活中的各种事件(无论是正面的如结婚,还是负面的如失业)按其所需的适应程度赋予压力值。发现累积的生活变化值与罹患疾病的风险存在显著相关。

▶
测试实验21、我知你心(埃克曼的“面部表情”研究)主要内容:通过对不同文化(包括与世界呼吸的某些部落)人群的研究,发现对于基本情绪(如愤怒、恐惧、快乐、悲伤、惊讶),其面部表情具有跨文化的一致性,支持了情绪表达的生物学基础。
▶
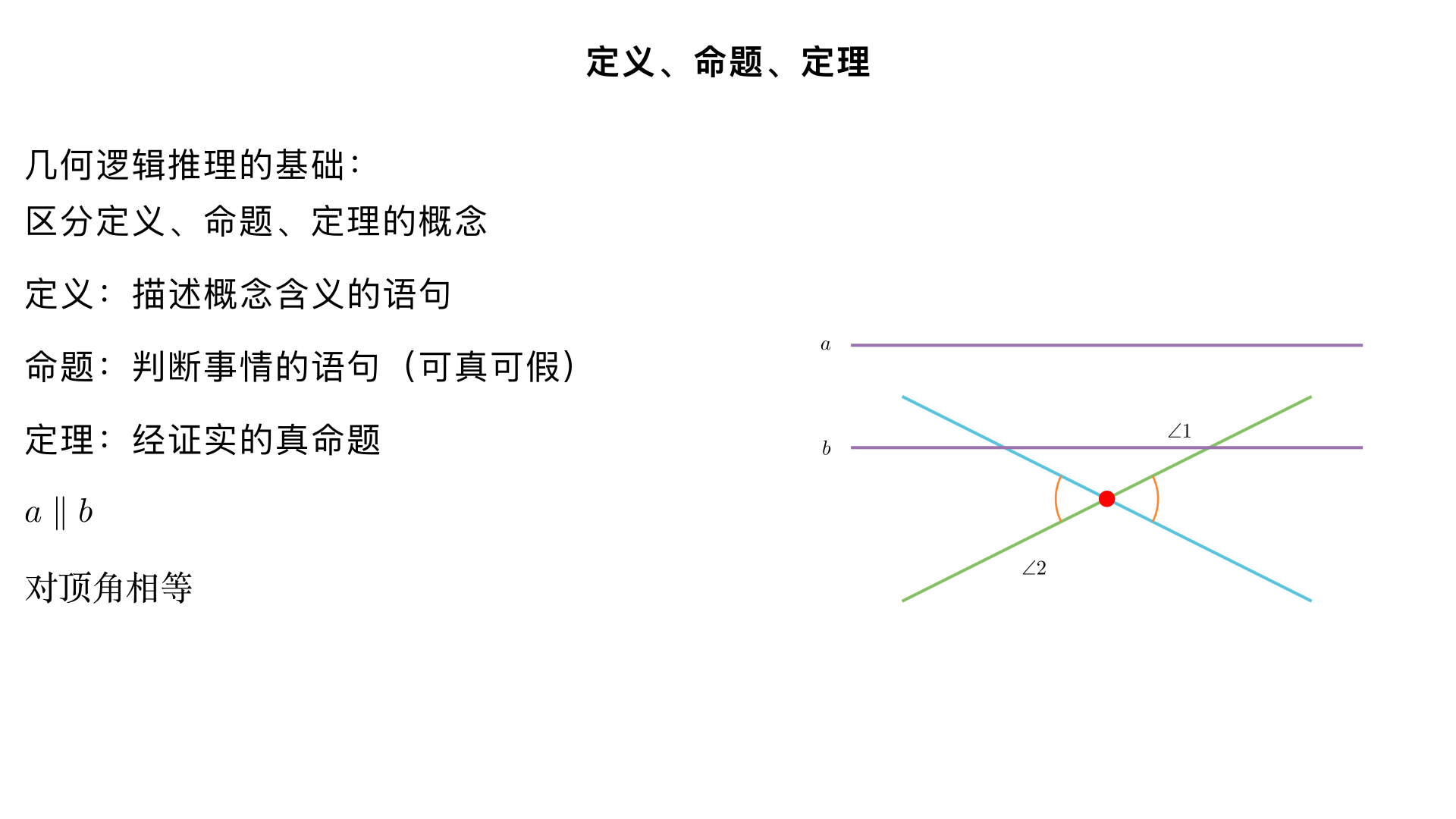
七年级数学・相交线与平行线・定义、命题、定理 本小节知识是几何逻辑推理的基础,核心是区分定义命题定理的概念,掌握命题的结构与真假判断,为后续平行线的推理证明铺垫。 一、核心定义 1. 相交线与平行线相关基础定义 相交线:在同一平面内,有且只有一个公共点的两条直线叫做相交线,这个公共点称为交点。 平行线:在同一平面内,不相交的两条直线叫做平行线,记作 a∥b ,读作 “a 平行于 b”。 对顶角:如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角叫做对顶角。 邻补角:两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角叫做邻补角。 2. 定义的本质 定义是对一个概念的含义进行准确描述的语句,它既可以作为判定依据,也可以作为性质使用。例如 “平行线的定义”,既可以用 “不相交” 判定两直线平行,也可以由 “两直线平行” 得出 “它们不相交” 的性质。 二、命题 1. 命题的定义 判断一件事情的语句叫做命题,命题必须是一个完整的陈述句,且能明确判断 “真” 或 “假”。 示例:“对顶角相等” 是命题;“画一条直线” 不是命题(未进行判断);“你好吗” 不是命题(不是陈述句)。 2. 命题的结构 任何命题都可以拆分为题设和结论两部分: 题设:命题中已知的事项(条件),通常用 “如果” 引导; 结论:由题设推出的事项(结果),通常用 “那么” 引导。 改写示例:将 “对顶角相等” 改写为 “如果两个角是对顶角,那么这两个角相等”,其中题设是 “两个角是对顶角”,结论是 “这两个角相等”。 3. 命题的分类 真命题:题设成立时,结论一定成立的命题,例如 “邻补角之和为 180°”; 假命题:题设成立时,结论不一定成立的命题,例如 “相等的角是对顶角”(反例:两直线平行时的同位角相等,但不是对顶角)。 三、定理 1. 定理的定义 经过推理证实的真命题叫做定理,定理可以作为后续推理证明的依据。 2. 相交线与平行线相关核心定理 (1)相交线相关定理 对顶角相等:如果两个角是对顶角,那么这两个角的度数相等。 邻补角互补:如果两个角是邻补角,那么它们的和为 180°。 (2)平行线相关定理 平行线的判定定理 同位角相等,两直线平行; 内错角相等,两直线平行; 同旁内角互补,两直线平行; 平行于同一条直线的两条直线互相平行。 平行线的性质定理 两直线平行,同位角相等; 两直线平行,内错角相等; 两直线平行,同旁内角互补。 四、定义、命题、定理的区别与联系 类别 核心特征 能否作为推理依据 定义 描述概念含义 能 命题 判断事情的语句(可真可假) 假命题不能,真命题未证实时也不能 定理 经证实的真命题 能
▶
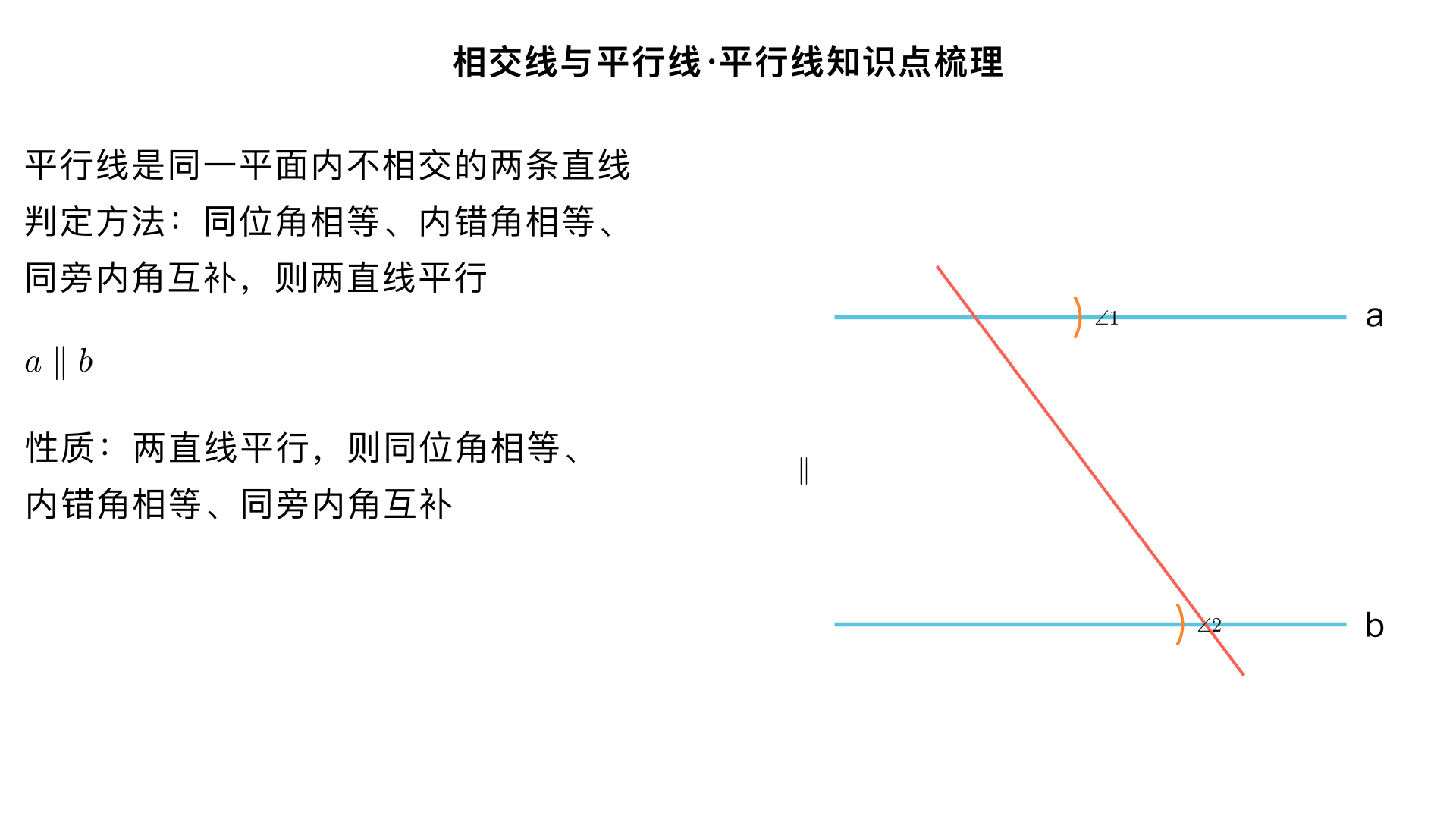
七年级数学・相交线与平行线・平行线知识点梳理 一、平行线的基本定义 在同一平面内,不相交的两条直线叫做平行线,记作 a∥b ,读作 “ a 平行于 b ”。 关键注意点 前提条件是同一平面内,若不在同一平面,不相交的直线不一定是平行线(如异面直线,七年级暂不涉及); 平行线是针对直线而言的,线段或射线的平行,是指它们所在的直线平行。 二、平行公理及推论 平行公理:经过直线外一点,有且只有一条直线与这条直线平行。 例:过直线 l 外一点 P ,只能画出一条直线与 l 平行。 平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。 符号语言:若 a∥c , b∥c ,则 a∥b 。 三、平行线的判定方法 判定平行线的核心是通过角的数量关系推导直线的位置关系,具体有以下 4 种判定方式: 同位角相等,两直线平行 定义:两条直线被第三条直线所截,若同位角相等,则这两条直线平行。 符号语言:若 ∠1=∠2 (同位角),则 a∥b 。 内错角相等,两直线平行 定义:两条直线被第三条直线所截,若内错角相等,则这两条直线平行。 符号语言:若 ∠3=∠4 (内错角),则 a∥b 。 同旁内角互补,两直线平行 定义:两条直线被第三条直线所截,若同旁内角之和为 180 ∘ ,则这两条直线平行。 符号语言:若 ∠5+∠6=180 ∘ (同旁内角),则 a∥b 。 平行公理推论的拓展判定:平行于同一直线的两直线平行(即上述平行公理推论)。 四、平行线的性质 平行线的性质与判定是互逆的,核心是通过直线的位置关系推导角的数量关系,具体有 3 条性质: 两直线平行,同位角相等 符号语言:若 a∥b ,则 ∠1=∠2 。 两直线平行,内错角相等 符号语言:若 a∥b ,则 ∠3=∠4 。 两直线平行,同旁内角互补 符号语言:若 a∥b ,则 ∠5+∠6=180 ∘ 。 五、平行线判定与性质的区别与联系 类别 判定 性质 逻辑关系 由角的关系推直线平行 由直线平行推角的关系 因果关系 因:角相等 / 互补;果:线平行 因:线平行;果:角相等 / 互补 核心用途 判断两条直线是否平行 计算角的度数或证明角的关系
▶
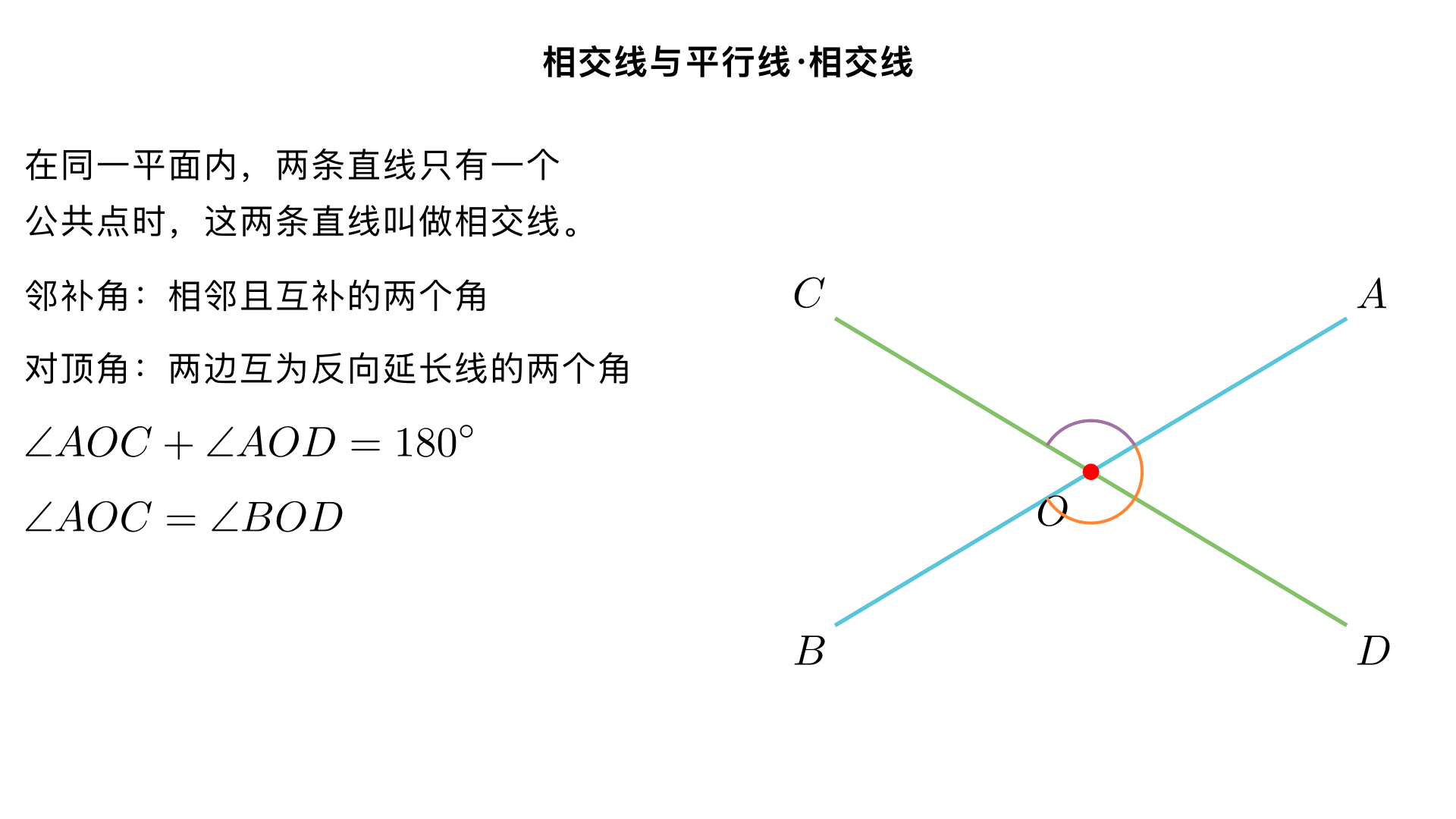
七年级数学・相交线与平行线・相交线 一、相交线的基本概念 相交线的定义在同一平面内,两条直线只有一个公共点时,这两条直线叫做相交线,这个公共点叫做交点。例如:直线 AB 和直线 CD 相交于点 O,点 O 就是它们的交点。 邻补角 定义:两条直线相交时,相邻且互补的两个角叫做邻补角。 特征:① 有一条公共边;② 另一边互为反向延长线;③ 两个角的和为 180°。 示例:直线 AB 与 CD 相交于 O,∠AOC 和∠AOD 是邻补角,∠AOC+∠AOD=180°。 对顶角 定义:两条直线相交时,一个角的两边分别是另一个角两边的反向延长线,这两个角叫做对顶角。 特征:① 顶点相同;② 两边互为反向延长线;③ 对顶角相等。 示例:直线 AB 与 CD 相交于 O,∠AOC 和∠BOD 是对顶角,则∠AOC=∠BOD;∠AOD 和∠BOC 是对顶角,则∠AOD=∠BOC。 二、垂线 垂线的定义如果两条直线相交所成的四个角中有一个角是直角(90°),那么这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。符号表示:若直线 AB⊥CD 于点 O,则∠AOC=90°。 垂线的性质 性质 1:在同一平面内,过一点有且只有一条直线与已知直线垂直。(“一点” 可以在直线上,也可以在直线外) 性质 2:连接直线外一点与直线上各点的所有线段中,垂线段最短,简称垂线段最短。 点到直线的距离从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。注意距离是 “长度”,是一个数值,而非线段本身。 三、相交线中的角度计算 核心依据 邻补角之和为 180°; 对顶角相等; 垂直的两条直线夹角为 90°。 典型例题已知直线 AB 和 CD 相交于点 O,OE⊥AB,∠EOD=65°,求∠AOC 的度数。解:∵OE⊥AB,∴∠AOE=90°∵∠AOE=∠AOD+∠EOD,∠EOD=65°∴∠AOD=90°-65°=25°又∵∠AOC 与∠AOD 是邻补角∴∠AOC=180°-25°=155°(或利用对顶角,若有其他条件也可灵活转换)
▶
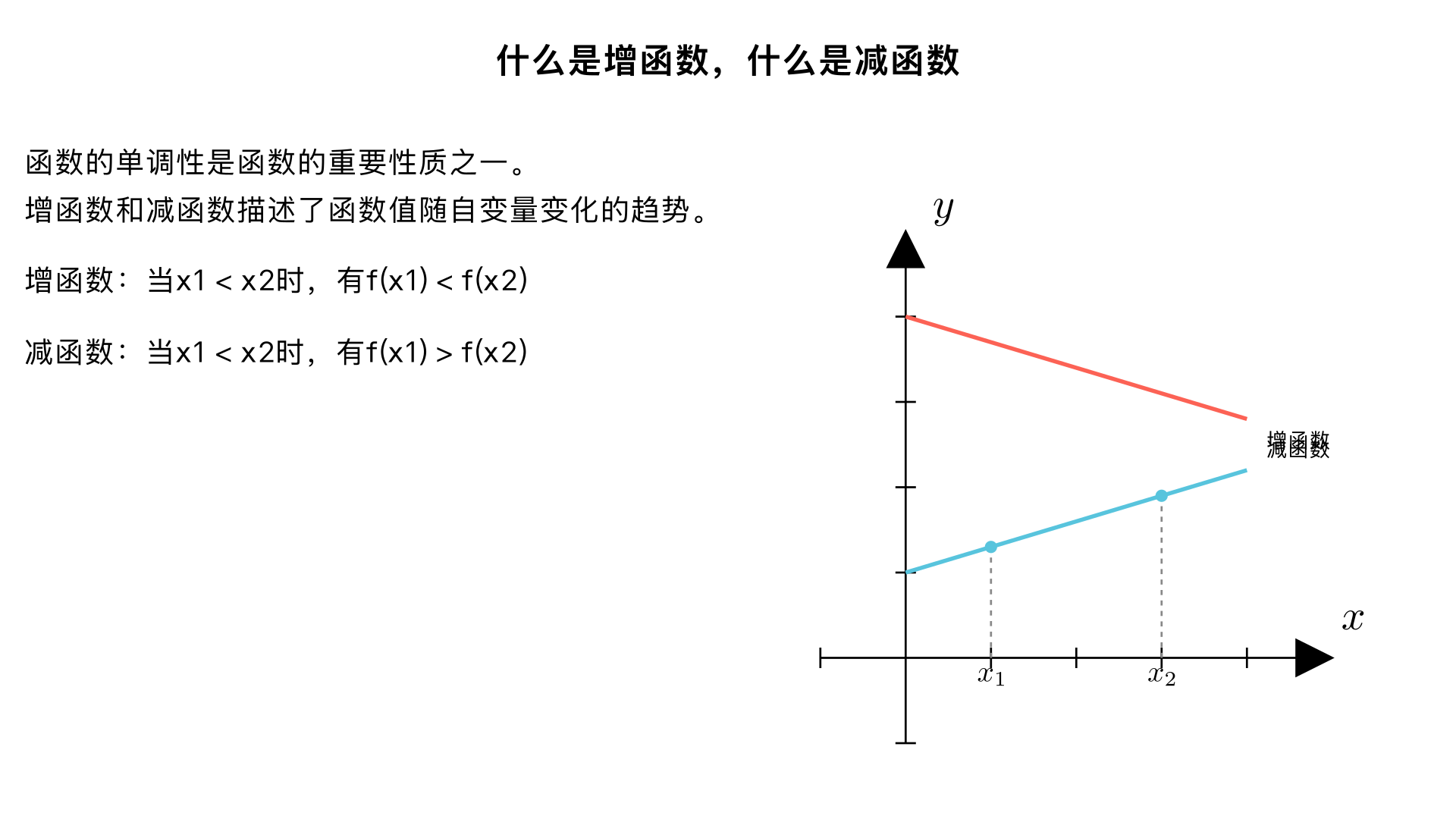
什么是增函数,什么是减函数
▶
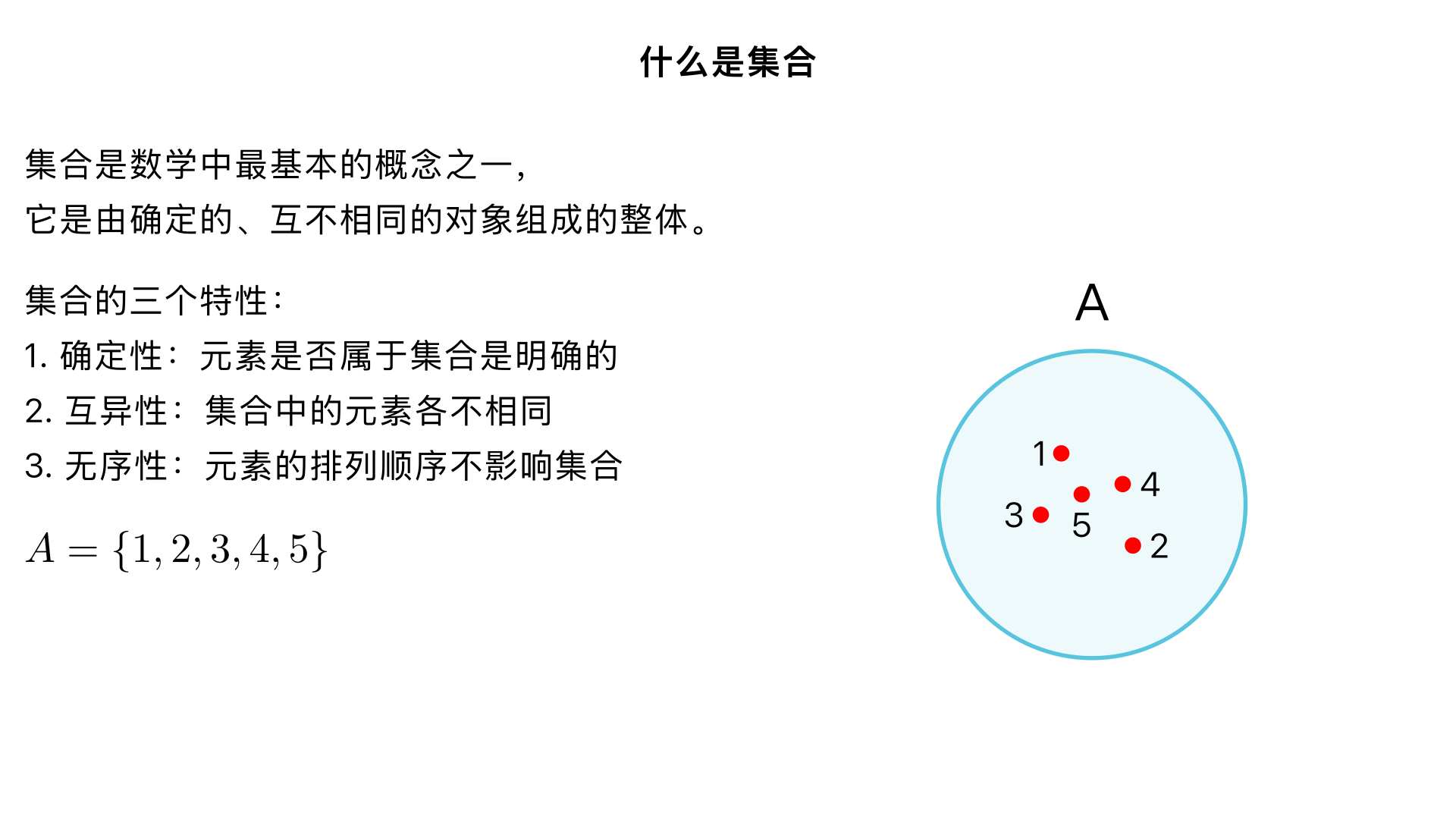
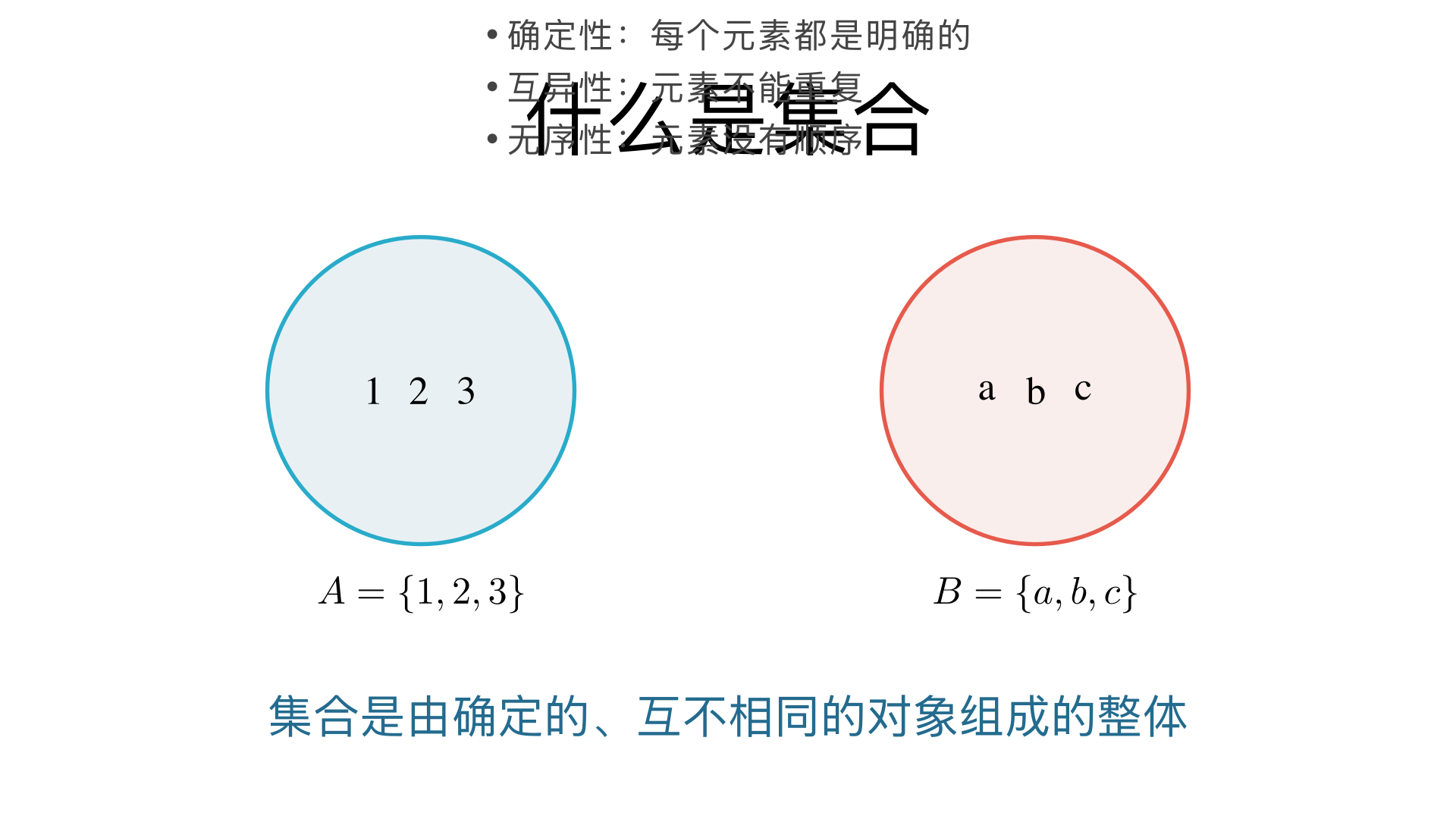
讲解什么是集合
▶
什么是集合
▶